全一卷
1.下列计算结果为5的是( )
A. | B. | C. | D. |
2.如图,将直角三角板 绕顶点A顺时针旋转到
绕顶点A顺时针旋转到 ,点
,点 恰好落在
恰好落在 的延长线上,
的延长线上, ,则
,则 为( )
为( )

 绕顶点A顺时针旋转到
绕顶点A顺时针旋转到 ,点
,点 恰好落在
恰好落在 的延长线上,
的延长线上, ,则
,则 为( )
为( )
A. | B. | C. | D. |
3.下列计算结果正确的是( )
A. | B. | C. | D. |
4.《孙子算经》中有“鸡兔同笼”问题:“今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何.”设鸡有x只,可列方程为( )
A. | B. |
C. | D. |
5.如图,在正五边形 中,以
中,以 为边向内作正
为边向内作正 ,则下列结论错误的是( )
,则下列结论错误的是( )

 中,以
中,以 为边向内作正
为边向内作正 ,则下列结论错误的是( )
,则下列结论错误的是( )
A. | B. | C. | D. |
6.为了解“睡眠管理”落实情况,某初中学校随机调查50名学生每天平均睡眠时间(时间均保留整数),将样本数据绘制成统计图(如图),其中有两个数据被遮盖关于睡眠时间的统计量中,与被遮盖的数据无关的是( )


| A.平均数 | B.中位数 | C.众数 | D.方差 |
7.如图,在 中,
中, 的平分线交
的平分线交 于点D,DE//AB,交
于点D,DE//AB,交 于点E,
于点E, 于点F,
于点F, ,则下列结论错误的是( )
,则下列结论错误的是( )

 中,
中, 的平分线交
的平分线交 于点D,DE//AB,交
于点D,DE//AB,交 于点E,
于点E, 于点F,
于点F, ,则下列结论错误的是( )
,则下列结论错误的是( )
A. | B. | C. | D. |
8.如图, 为
为 的直径,弦
的直径,弦 于点E,
于点E, 于点F,
于点F, ,则
,则 为( )
为( )

 为
为 的直径,弦
的直径,弦 于点E,
于点E, 于点F,
于点F, ,则
,则 为( )
为( )
A. | B. | C. | D. |
9.已知 ,且
,且 ,则
,则 的值是( )
的值是( )
 ,且
,且 ,则
,则 的值是( )
的值是( )A. | B. | C. | D. |
10.已知点 在抛物线
在抛物线 上,当
上,当 且
且 时,都有
时,都有 ,则m的取值范围为( )
,则m的取值范围为( )
 在抛物线
在抛物线 上,当
上,当 且
且 时,都有
时,都有 ,则m的取值范围为( )
,则m的取值范围为( )A. | B. | C. | D. |
11.比较大小:
_______________  .(选填>,=,<)
.(选填>,=,<)

 .(选填>,=,<)
.(选填>,=,<)12.老师为帮助学生正确理解物理变化与化学变化,将6种生活现象制成看上去无差别卡片(如图).从中随机抽取一张卡片,抽中生活现象是物理变化的概率是_______________ .


13.数学实践活动中,为了测量校园内被花坛隔开的A,B两点的距离,同学们在 外选择一点C,测得
外选择一点C,测得 两边中点的距离
两边中点的距离 为
为 (如图),则A,B两点的距离是
(如图),则A,B两点的距离是_______________ m.

 外选择一点C,测得
外选择一点C,测得 两边中点的距离
两边中点的距离 为
为 (如图),则A,B两点的距离是
(如图),则A,B两点的距离是
14.若 为整数,x为正整数,则x的值是
为整数,x为正整数,则x的值是_______________ .
 为整数,x为正整数,则x的值是
为整数,x为正整数,则x的值是15.如图,水池中心点O处竖直安装一水管,水管喷头喷出抛物线形水柱,喷头上下移动时,抛物线形水柱随之竖直上下平移,水柱落点与点O在同一水平面.安装师傅调试发现,喷头高 时,水柱落点距O点
时,水柱落点距O点 ;喷头高
;喷头高 时,水柱落点距O点
时,水柱落点距O点 .那么喷头高
.那么喷头高_______________ m时,水柱落点距O点 .
.

 时,水柱落点距O点
时,水柱落点距O点 ;喷头高
;喷头高 时,水柱落点距O点
时,水柱落点距O点 .那么喷头高
.那么喷头高 .
.
16.如图,正方形 边长为1,点E在边
边长为1,点E在边 上(不与A,B重合),将
上(不与A,B重合),将 沿直线
沿直线 折叠,点A落在点
折叠,点A落在点 处,连接
处,连接 ,将
,将 绕点B顺时针旋转
绕点B顺时针旋转 得到
得到 ,连接
,连接 .给出下列四个结论:①
.给出下列四个结论:① ;②
;② ;③点P是直线
;③点P是直线 上动点,则
上动点,则 的最小值为
的最小值为 ;④当
;④当 时,
时, 的面积
的面积 .其中正确的结论是
.其中正确的结论是_______________ .(填写序号)

 边长为1,点E在边
边长为1,点E在边 上(不与A,B重合),将
上(不与A,B重合),将 沿直线
沿直线 折叠,点A落在点
折叠,点A落在点 处,连接
处,连接 ,将
,将 绕点B顺时针旋转
绕点B顺时针旋转 得到
得到 ,连接
,连接 .给出下列四个结论:①
.给出下列四个结论:① ;②
;② ;③点P是直线
;③点P是直线 上动点,则
上动点,则 的最小值为
的最小值为 ;④当
;④当 时,
时, 的面积
的面积 .其中正确的结论是
.其中正确的结论是
17.先化简,再求值: ,其中
,其中 .
.
 ,其中
,其中 .
.18.如图,在菱形 中,点E,F分别在边
中,点E,F分别在边 上,
上, ,
, 分别与
分别与 交于点M,N.求证:
交于点M,N.求证:

(1) .
.
(2) .
.
 中,点E,F分别在边
中,点E,F分别在边 上,
上, ,
, 分别与
分别与 交于点M,N.求证:
交于点M,N.求证:
(1)
 .
.(2)
 .
.19.为传播数学文化,激发学生学习兴趣,学校开展数学学科月活动,七年级开展了四个项目:A.阅读数学名著;B.讲述数学故事;C.制作数学模型;D.挑战数学游戏要求七年级学生每人只能参加一项.为了解学生参加各项目情况,随机调查了部分学生,将调查结果制作成统计表和扇形统计图(如图),请根据图表信息解答下列问题:

(1) _______________,
_______________, _______________.
_______________.
(2)扇形统计图中“B”项目所对应的扇形圆心角为_______________度.
(3)在月末的展示活动中,“C”项目中七(1)班有3人获得一等奖,七(2)班有2人获得一等奖,现从这5名学生中随机抽取2人代表七年级参加学校制作数学模型比赛,请用列表或画树状图法求抽中的2名学生来自不同班级的概率.
| 项目 | A | B | C | D |
| 人数/人 | 5 | 15 | a | b |

(1)
 _______________,
_______________, _______________.
_______________.(2)扇形统计图中“B”项目所对应的扇形圆心角为_______________度.
(3)在月末的展示活动中,“C”项目中七(1)班有3人获得一等奖,七(2)班有2人获得一等奖,现从这5名学生中随机抽取2人代表七年级参加学校制作数学模型比赛,请用列表或画树状图法求抽中的2名学生来自不同班级的概率.
20.已知关于x的一元二次方程 有实数根.
有实数根.
(1)求实数k的取值范围.
(2)设方程的两个实数根分别为 ,若
,若 ,求k的值.
,求k的值.
 有实数根.
有实数根.(1)求实数k的取值范围.
(2)设方程的两个实数根分别为
 ,若
,若 ,求k的值.
,求k的值.21.如图,直线 与双曲线交于
与双曲线交于 两点,直线
两点,直线 与双曲线在第一象限交于点C,连接
与双曲线在第一象限交于点C,连接 .
.

(1)求直线 与双曲线的解析式.
与双曲线的解析式.
(2)求 的面积.
的面积.
 与双曲线交于
与双曲线交于 两点,直线
两点,直线 与双曲线在第一象限交于点C,连接
与双曲线在第一象限交于点C,连接 .
.
(1)求直线
 与双曲线的解析式.
与双曲线的解析式.(2)求
 的面积.
的面积.22.如图, 为
为 的直径,点C是
的直径,点C是 上一点,点D是
上一点,点D是 外一点,
外一点, ,连接
,连接 交
交 于点E.
于点E.

(1)求证: 是
是 的切线.
的切线.
(2)若 ,求
,求 的值.
的值.
 为
为 的直径,点C是
的直径,点C是 上一点,点D是
上一点,点D是 外一点,
外一点, ,连接
,连接 交
交 于点E.
于点E.
(1)求证:
 是
是 的切线.
的切线.(2)若
 ,求
,求 的值.
的值.23.南充市被誉为中国绸都,本地某电商销售真丝衬衣和真丝围巾两种产品,它们的进价和售价如下表用15000元可购进真丝衬衣50件和真丝围巾25件.(利润=售价-进价)
(1)求真丝衬衣进价a的值.
(2)若该电商计划购进真丝衬衣和真丝围巾两种商品共300件,据市场销售分析,真丝围巾进货件数不低于真丝衬衣件数的2倍.如何进货才能使本次销售获得的利润最大?最大利润是多少元?
(3)按(2)中最大利润方案进货与销售,在实际销售过程中,当真丝围巾销量达到一半时,为促销并保证销售利润不低于原来最大利润的90%,衬衣售价不变,余下围巾降价销售,每件最多降价多少元?
| 种类 | 真丝衬衣 | 真丝围巾 |
| 进价(元/件) | a | 80 |
| 售价(元/件) | 300 | 100 |
(1)求真丝衬衣进价a的值.
(2)若该电商计划购进真丝衬衣和真丝围巾两种商品共300件,据市场销售分析,真丝围巾进货件数不低于真丝衬衣件数的2倍.如何进货才能使本次销售获得的利润最大?最大利润是多少元?
(3)按(2)中最大利润方案进货与销售,在实际销售过程中,当真丝围巾销量达到一半时,为促销并保证销售利润不低于原来最大利润的90%,衬衣售价不变,余下围巾降价销售,每件最多降价多少元?
24.如图,在矩形 中,点O是
中,点O是 的中点,点M是射线
的中点,点M是射线 上动点,点P在线段
上动点,点P在线段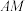 上(不与点A重合),
上(不与点A重合), .
.

(1)判断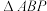 的形状,并说明理由.
的形状,并说明理由.
(2)当点M为边 中点时,连接
中点时,连接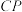 并延长交
并延长交 于点N.求证:
于点N.求证: .
.
(3)点Q在边 上,
上, ,当
,当 时,求
时,求 的长.
的长.
 中,点O是
中,点O是 的中点,点M是射线
的中点,点M是射线 上动点,点P在线段
上动点,点P在线段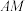 上(不与点A重合),
上(不与点A重合), .
.
(1)判断
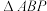 的形状,并说明理由.
的形状,并说明理由.(2)当点M为边
 中点时,连接
中点时,连接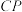 并延长交
并延长交 于点N.求证:
于点N.求证: .
.(3)点Q在边
 上,
上, ,当
,当 时,求
时,求 的长.
的长.25.抛物线 与x轴分别交于点
与x轴分别交于点 ,与y轴交于点
,与y轴交于点 .
.

(1)求抛物线的解析式.
(2)如图1, 顶点P在抛物线上,如果
顶点P在抛物线上,如果 面积为某值时,符合条件的点P有且只有三个,求点P的坐标.
面积为某值时,符合条件的点P有且只有三个,求点P的坐标.
(3)如图2,点M在第二象限的抛物线上,点N在 延长线上,
延长线上, ,连接
,连接 并延长到点D,使
并延长到点D,使 .
. 交x轴于点E,
交x轴于点E, 与
与 均为锐角,
均为锐角, ,求点M的坐标.
,求点M的坐标.
 与x轴分别交于点
与x轴分别交于点 ,与y轴交于点
,与y轴交于点 .
.
(1)求抛物线的解析式.
(2)如图1,
 顶点P在抛物线上,如果
顶点P在抛物线上,如果 面积为某值时,符合条件的点P有且只有三个,求点P的坐标.
面积为某值时,符合条件的点P有且只有三个,求点P的坐标.(3)如图2,点M在第二象限的抛物线上,点N在
 延长线上,
延长线上, ,连接
,连接 并延长到点D,使
并延长到点D,使 .
. 交x轴于点E,
交x轴于点E, 与
与 均为锐角,
均为锐角, ,求点M的坐标.
,求点M的坐标. 搜索
搜索
 难度系数:0.94
难度系数:0.94  答案解析
答案解析
 有奖纠错
有奖纠错
