搜索
全一卷
难度系数：0.94 
答案解析
有奖纠错
1．如图，点
、
表示的实数互为相反数，则点表示的实数是（ ）
、表示的实数互为相反数，则点表示的实数是（ ）| A．2 | B．－2 | C． | D． |
2．下列整式与
为同类项的是（ ）
为同类项的是（ ）A． | B． | C． | D． |
3．“冰墩墩”是北京2022年冬季奥运会的吉祥物．该吉祥物以熊猫为原型进行设计创作，将熊猫形象与富有超能量的冰晶外壳相结合，体现了冬季冰雪运动和现代科技特点，冰墩墩玩具也很受欢迎．某玩具店一个星期销售冰墩墩玩具数量如下：
则这个星期该玩具店销售冰墩墩玩具的平均数和中位数分别是（ ）
星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期日 | |
玩具数量（件） | 35 | 47 | 50 | 48 | 42 | 60 | 68 |
则这个星期该玩具店销售冰墩墩玩具的平均数和中位数分别是（ ）
| A．48，47 | B．50，47 | C．50，48 | D．48，50 |
4．为培养青少年的创新意识、动手实践能力、现场应变能力和团队精神，湘潭市举办了第10届青少年机器人竞赛．组委会为每个比赛场地准备了四条腿的桌子和三条腿的凳子共12个，若桌子腿数与凳子腿数的和为40条，则每个比赛场地有几张桌子和几条凳子？设有
张桌子，有
条凳子，根据题意所列方程组正确的是（ ）
张桌子，有条凳子，根据题意所列方程组正确的是（ ）A． | B． |
C． | D． |
5．在
中（如图），连接
，已知
，
，则
（ ）
中（如图），连接，已知，，则（ ）A． | B． | C． | D． |
6．在
中（如图），点
、
分别为
、的中点，则
（ ）
中（如图），点、分别为、的中点，则（ ）A． | B． | C． | D． |
7．中国古代数学家赵爽在为《周髀算经》作注解时，用4个全等的直角三角形拼成正方形（如图），并用它证明了勾股定理，这个图被称为“弦图”．若“弦图”中小正方形面积与每个直角三角形面积均为1，
为直角三角形中的一个锐角，则
（ ）
为直角三角形中的一个锐角，则
（ ）
| A．2 | B． | C． | D． |
8．若
，则下列四个选项中一定成立的是（ ）
，则下列四个选项中一定成立的是（ ）A． | B． | C． | D． |
9．依据“双减”政策要求，初中学生书面作业每天完成时间不超过90分钟．某中学为了解学生作业管理情况，抽查了七年级（一）班全体同学某天完成作业时长情况，绘制出如图所示的频数直方图：（数据分成3组：
，
，
）．则下列说法正确的是（ ）
，，）．则下列说法正确的是（ ）| A．该班有40名学生 |
| B．该班学生当天完成作业时长在分钟的人数最多 |
| C．该班学生当天完成作业时长在分钟的频数是5 |
D．该班学生当天完成作业时长在 分钟的人数占全班人数的 |
10．下列计算正确的是（ ）
A． | B． | C． | D． |
11．如图，小明在学了尺规作图后，作了一个图形，其作图步骤是：①作线段
，分别以点、为圆心，以长为半径画弧，两弧相交于点
、；②连接、
，作直线
，且与相交于点
．则下列说法正确的是（ ）
，分别以点、为圆心，以长为半径画弧，两弧相交于点、；②连接、，作直线，且与相交于点．则下列说法正确的是（ ）| A．是等边三角形 | B． |
C． | D． |
12．四个数－1，0，，
中，为无理数的是_________ ．
，中，为无理数的是13．请写出一个随增大而增大的一次函数表达式_________ ．
随增大而增大的一次函数表达式14．如图，一束光沿方向，先后经过平面镜
、
反射后，沿
方向射出，已知
，
，则
_________ ．
方向，先后经过平面镜、反射后，沿方向射出，已知，，则15．如图，在平面直角坐标系中，已知的三个顶点的坐标分别为
，
，
．将绕原点
顺时针旋转
后得到
．
(1)请写出
、
、
三点的坐标：_________，_________，_________
(2)求点旋转到点的弧长．
的三个顶点的坐标分别为，，．将绕原点顺时针旋转后得到．(1)请写出
、、三点的坐标：_________，_________，_________(2)求点
旋转到点的弧长．16．如图，在⊙中，直径与弦相交于点，连接、
．
(1)求证：
；
(2)连接
，若
，
，求⊙的半径．
中，直径与弦相交于点，连接、．(1)求证：
；(2)连接
，若，，求⊙的半径．17．5月30日是全国科技工作者日，某校准备举办“走近科技英雄，讲好中国故事”的主题比赛活动．八年级（一）班由、
、
三名同学在班上进行初赛，推荐排名前两位的同学参加学校决赛．
(1)请写出在班上初赛时，这三名同学讲故事顺序的所有可能结果；
(2)若、两名同学参加学校决赛，学校制作了编号为、、的3张卡片（如图，除编号和内容外，其余完全相同），放在一个不透明的盒子里．先由随机摸取1张卡片记下编号，然后放回，再由随机摸取1张卡片记下编号，根据摸取的卡片内容讲述相关英雄的故事．求、两人恰好讲述同一名科技英雄故事的概率．（请用“画树状图”或“列表”等方法写出分析过程）
、、三名同学在班上进行初赛，推荐排名前两位的同学参加学校决赛．(1)请写出在班上初赛时，这三名同学讲故事顺序的所有可能结果；
(2)若
、两名同学参加学校决赛，学校制作了编号为、、的3张卡片（如图，除编号和内容外，其余完全相同），放在一个不透明的盒子里．先由随机摸取1张卡片记下编号，然后放回，再由随机摸取1张卡片记下编号，根据摸取的卡片内容讲述相关英雄的故事．求、两人恰好讲述同一名科技英雄故事的概率．（请用“画树状图”或“列表”等方法写出分析过程）| A“杂交水稻之父”袁隆平 | B“天眼之父”南仁东 | C“航天之父”钱学森 |
18．湘潭县石鼓油纸伞因古老工艺和文化底蕴，已成为石鼓乡村旅游的一张靓丽名片．某中学八年级数学兴趣小组参观后，进行了设计伞的实践活动．小文依据黄金分割的美学设计理念，设计了中截面如图所示的伞骨结构（其中
）：伞柄
始终平分
，
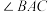，当
时，伞完全打开，此时
．请问最少需要准备多长的伞柄？（结果保留整数，参考数据：
）
）：伞柄
始终平分
，
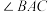，当
时，伞完全打开，此时
．请问最少需要准备多长的伞柄？（结果保留整数，参考数据：
）
19．百年青春百年梦，初心献党向未来．为热烈庆祝中国共产主义青年团成立100周年，继承先烈遗志，传承“五四”精神．某中学在“做新时代好少年，强国有我”的系列活动中，开展了“好书伴我成长”的读书活动．为了解5月份八年级学生的读书情况，随机调查了八年级20名学生读书数量（单位：本），并进行了以下数据的整理与分析：
数据收集：2 5 3 5 4 6 1 5 3 4 3 6 7 5 8 3 4 7 3 4
数据整理：
数据分析：绘制成不完整的扇形统计图：
依据统计信息回答问题
(1)在统计表中，
_________；
(2)在扇形统计图中，
部分对应的圆心角的度数为_________；
(3)若该校八年级学生人数为200人，请根据上述调查结果，估计该校八年级学生读书在4本以上的人数．
数据收集：2 5 3 5 4 6 1 5 3 4 3 6 7 5 8 3 4 7 3 4
数据整理：
| 本数 |  |  |  |  |
| 组别 |  |  |  |  |
| 频数 | 2 |  | 6 | 3 |
数据分析：绘制成不完整的扇形统计图：
依据统计信息回答问题
(1)在统计表中，
_________；(2)在扇形统计图中，
部分对应的圆心角的度数为_________；(3)若该校八年级学生人数为200人，请根据上述调查结果，估计该校八年级学生读书在4本以上的人数．
20．为落实国家《关于全面加强新时代大中小学劳动教育的意见》，某校准备在校园里利用围墙（墙长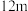
）和
长的篱笆墙，围成Ⅰ、Ⅱ两块矩形劳动实践基地．某数学兴趣小组设计了两种方案（除围墙外，实线部分为篱笆墙，且不浪费篱笆墙），请根据设计方案回答下列问题：
(1)方案一：如图①，全部利用围墙的长度，但要在Ⅰ区中留一个宽度
的水池且需保证总种植面积为
，试分别确定
、
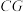的长；
(2)方案二：如图②，使围成的两块矩形总种植面积最大，请问
应设计为多长？此时最大面积为多少？
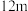）和
长的篱笆墙，围成Ⅰ、Ⅱ两块矩形劳动实践基地．某数学兴趣小组设计了两种方案（除围墙外，实线部分为篱笆墙，且不浪费篱笆墙），请根据设计方案回答下列问题：
(1)方案一：如图①，全部利用围墙的长度，但要在Ⅰ区中留一个宽度
的水池且需保证总种植面积为
，试分别确定
、
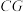的长；(2)方案二：如图②，使围成的两块矩形总种植面积最大，请问
应设计为多长？此时最大面积为多少？21．已知
、
是平面直角坐标系中两点，连接
．
(1)如图①，点
在线段上，以点为圆心的圆与两条坐标轴都相切，求过点的反比例函数表达式；
(2)如图②，点
是线段
上一点，连接
，将
沿翻折，使得点
与线段上的点
重合，求经过
、两点的一次函数表达式．
、
是平面直角坐标系中两点，连接
．
(1)如图①，点
在线段上，以点为圆心的圆与两条坐标轴都相切，求过点的反比例函数表达式；(2)如图②，点
是线段
上一点，连接
，将
沿翻折，使得点
与线段上的点
重合，求经过、两点的一次函数表达式．22．在中，
，
，直线
经过点，过点、分别作的垂线，垂足分别为点、．
(1)特例体验：
如图①，若直线
，
，分别求出线段、
和
的长；
(2)规律探究：
①如图②，若直线从图①状态开始绕点旋转
，请探究线段、和的数量关系并说明理由；
②如图③，若直线从图①状态开始绕点A顺时针旋转
，与线段相交于点，请再探线段、和的数量关系并说明理由；
(3)尝试应用：
在图③中，延长线段交线段于点
，若
，
，求
．
中，，，直线经过点，过点、分别作的垂线，垂足分别为点、．(1)特例体验：
如图①，若直线
，，分别求出线段、和的长；(2)规律探究：
①如图②，若直线
从图①状态开始绕点旋转，请探究线段、和的数量关系并说明理由；②如图③，若直线
从图①状态开始绕点A顺时针旋转，与线段相交于点，请再探线段、和的数量关系并说明理由；(3)尝试应用：
在图③中，延长线段
交线段于点，若，，求．23．已知抛物线
．
(1)如图①，若抛物线图象与轴交于点
，与轴交点
．连接．
①求该抛物线所表示的二次函数表达式；
②若点
是抛物线上一动点（与点不重合），过点作
轴于点，与线段交于点
．是否存在点使得点是线段
的三等分点？若存在，请求出点的坐标；若不存在，请说明理由．
(2)如图②，直线
与轴交于点，同时与抛物线交于点
，以线段为边作菱形
，使点落在轴的正半轴上，若该抛物线与线段没有交点，求
的取值范围．
．(1)如图①，若抛物线图象与
轴交于点，与轴交点．连接．①求该抛物线所表示的二次函数表达式；
②若点
是抛物线上一动点（与点不重合），过点作轴于点，与线段交于点．是否存在点使得点是线段的三等分点？若存在，请求出点的坐标；若不存在，请说明理由．(2)如图②，直线
与轴交于点，同时与抛物线交于点，以线段为边作菱形，使点落在轴的正半轴上，若该抛物线与线段没有交点，求的取值范围．24．下列几何体中，主视图为三角形的是（ ）
A． | B． | C． | D． |
25．2022年6月5日，神舟十四号载人飞船在酒泉卫星发射中心发射成功，飞船入轨后将按照预定程序与离地面约400000米的天宫空间站进行对接．请将400000米用科学记数法表示为_________ 米．
26．先化简，再求值：
，其中
．
，其中．