全一卷
1.下列四个数中,最小的数是( )
| A.0 | B.-2 | C.1 | D. |
2.在以下“绿色食品、响应环保、可回收物、节水”四个标志图案中,是轴对称图形的是( )
A. | B. | C. | D. |
3.2022年5月19日,达州金垭机场正式通航.金亚机场位于达州高新区,占地总面积2940亩,概算投资约为26.62亿元.数据26.62亿元用科学记数法表示为( )
A. 元 元 | B. 元 元 | C. 元 元 | D. 元 元 |
4.如图, ,直线
,直线 分别交
分别交 ,
, 于点M,N,将一个含有45°角的直角三角尺按如图所示的方式摆放,若
于点M,N,将一个含有45°角的直角三角尺按如图所示的方式摆放,若 ,则
,则 等于( )
等于( )

 ,直线
,直线 分别交
分别交 ,
, 于点M,N,将一个含有45°角的直角三角尺按如图所示的方式摆放,若
于点M,N,将一个含有45°角的直角三角尺按如图所示的方式摆放,若 ,则
,则 等于( )
等于( )
| A.15° | B.25° | C.35° | D.45° |
5.中国清代算书《御制数理精蕴》中有这样一题:“马四匹、牛六头,共价四十八两(‘两’为我国古代货币单位);马二匹、牛五头,共价三十八两,阀马、牛各价几何?”设马每匹x两,牛每头y两,根据题意可列方程组为( )
A. | B. | C. | D. |
6.下列命题是真命题的是( )
| A.相等的两个角是对顶角 |
| B.相等的圆周角所对的弧相等 |
C.若 ,则 ,则 |
D.在一个不透明的箱子里放有1个白球和2个红球,它们除颜色外其余都相同,从箱子里任意摸出1个球,摸到白球的概率是 |
7.如图,在 中,点D,E分别是
中,点D,E分别是 ,
, 边的中点,点F在
边的中点,点F在 的延长线上.添加一个条件,使得四边形
的延长线上.添加一个条件,使得四边形 为平行四边形,则这个条件可以是( )
为平行四边形,则这个条件可以是( )

 中,点D,E分别是
中,点D,E分别是 ,
, 边的中点,点F在
边的中点,点F在 的延长线上.添加一个条件,使得四边形
的延长线上.添加一个条件,使得四边形 为平行四边形,则这个条件可以是( )
为平行四边形,则这个条件可以是( )
A. | B. | C. | D. |
8.如图,点E在矩形 的
的 边上,将
边上,将 沿
沿 翻折,点A恰好落在
翻折,点A恰好落在 边上的点F处,若
边上的点F处,若 ,
, ,则
,则 的长为( )
的长为( )

 的
的 边上,将
边上,将 沿
沿 翻折,点A恰好落在
翻折,点A恰好落在 边上的点F处,若
边上的点F处,若 ,
, ,则
,则 的长为( )
的长为( )
| A.9 | B.12 | C.15 | D.18 |
9.如图所示的曲边三角形可按下述方法作出:作等边 ,分别以点A,B,C为圆心,以
,分别以点A,B,C为圆心,以 长为半径作
长为半径作 ,
, ,
, ,三弧所围成的图形就是一个曲边三角形.如果一个曲边三角形的周长为
,三弧所围成的图形就是一个曲边三角形.如果一个曲边三角形的周长为 ,则此曲边三角形的面积为( )
,则此曲边三角形的面积为( )

 ,分别以点A,B,C为圆心,以
,分别以点A,B,C为圆心,以 长为半径作
长为半径作 ,
, ,
, ,三弧所围成的图形就是一个曲边三角形.如果一个曲边三角形的周长为
,三弧所围成的图形就是一个曲边三角形.如果一个曲边三角形的周长为 ,则此曲边三角形的面积为( )
,则此曲边三角形的面积为( )
A. | B. | C. | D. |
10.二次函数 的部分图象如图所示,与y轴交于
的部分图象如图所示,与y轴交于 ,对称轴为直线
,对称轴为直线 .以下结论:①
.以下结论:① ;②
;② ;③对于任意实数m,都有
;③对于任意实数m,都有 成立;④若
成立;④若 ,
, ,
, 在该函数图象上,则
在该函数图象上,则 ;⑤方程
;⑤方程 (
( ,k为常数)的所有根的和为4.其中正确结论有( )
,k为常数)的所有根的和为4.其中正确结论有( )

 的部分图象如图所示,与y轴交于
的部分图象如图所示,与y轴交于 ,对称轴为直线
,对称轴为直线 .以下结论:①
.以下结论:① ;②
;② ;③对于任意实数m,都有
;③对于任意实数m,都有 成立;④若
成立;④若 ,
, ,
, 在该函数图象上,则
在该函数图象上,则 ;⑤方程
;⑤方程 (
( ,k为常数)的所有根的和为4.其中正确结论有( )
,k为常数)的所有根的和为4.其中正确结论有( )
| A.2 | B.3 | C.4 | D.5 |
11.计算:
______ .

12.如图,在 中,
中, ,
, ,分别以点A,B为圆心,大于
,分别以点A,B为圆心,大于 的长为半径作弧,两弧分别相交于点M,N,作直线
的长为半径作弧,两弧分别相交于点M,N,作直线 ,交
,交 于点D,连接
于点D,连接 ,则
,则 的度数为
的度数为_____ .

 中,
中, ,
, ,分别以点A,B为圆心,大于
,分别以点A,B为圆心,大于 的长为半径作弧,两弧分别相交于点M,N,作直线
的长为半径作弧,两弧分别相交于点M,N,作直线 ,交
,交 于点D,连接
于点D,连接 ,则
,则 的度数为
的度数为
13.如图,菱形 的对角线
的对角线 与
与 相交于点
相交于点 ,
, ,
, ,则菱形
,则菱形 的周长是
的周长是________ .

 的对角线
的对角线 与
与 相交于点
相交于点 ,
, ,
, ,则菱形
,则菱形 的周长是
的周长是
14.关于x的不等式组 恰有3个整数解,则a的取值范围是
恰有3个整数解,则a的取值范围是_______ .
 恰有3个整数解,则a的取值范围是
恰有3个整数解,则a的取值范围是15.人们把 这个数叫做黄金比,著名数学家华罗庚优选法中的“0.618法”就应用了黄金比.设
这个数叫做黄金比,著名数学家华罗庚优选法中的“0.618法”就应用了黄金比.设 ,
, ,记
,记 ,
, ,…,
,…, ,则
,则
_______ .
 这个数叫做黄金比,著名数学家华罗庚优选法中的“0.618法”就应用了黄金比.设
这个数叫做黄金比,著名数学家华罗庚优选法中的“0.618法”就应用了黄金比.设 ,
, ,记
,记 ,
, ,…,
,…, ,则
,则
16.如图,在边长为2的正方形 中,点E,F分别为
中,点E,F分别为 ,
, 边上的动点(不与端点重合),连接
边上的动点(不与端点重合),连接 ,
, ,分别交对角线
,分别交对角线 于点P,Q.点E,F在运动过程中,始终保持
于点P,Q.点E,F在运动过程中,始终保持 ,连接
,连接 ,
, ,
, .以下结论:①
.以下结论:① ;②
;② ;③
;③ ;④
;④ 为等腰直角三角形;⑤若过点B作
为等腰直角三角形;⑤若过点B作 ,垂足为H,连接
,垂足为H,连接 ,则
,则 的最小值为
的最小值为 .其中所有正确结论的序号是
.其中所有正确结论的序号是____ .

 中,点E,F分别为
中,点E,F分别为 ,
, 边上的动点(不与端点重合),连接
边上的动点(不与端点重合),连接 ,
, ,分别交对角线
,分别交对角线 于点P,Q.点E,F在运动过程中,始终保持
于点P,Q.点E,F在运动过程中,始终保持 ,连接
,连接 ,
, ,
, .以下结论:①
.以下结论:① ;②
;② ;③
;③ ;④
;④ 为等腰直角三角形;⑤若过点B作
为等腰直角三角形;⑤若过点B作 ,垂足为H,连接
,垂足为H,连接 ,则
,则 的最小值为
的最小值为 .其中所有正确结论的序号是
.其中所有正确结论的序号是
17.计算: .
.
 .
.18.化简求值: ,其中
,其中 .
.
 ,其中
,其中 .
.19.“防溺水”是校园安全教育工作的重点之一.某校为确保学生安全,开展了“远离溺水·珍爱生命”的防溺水安全知识竞赛.现从该校七、八年级中各随机抽取10名学生的竞赛成绩(百分制)进行整理和分析(成绩得分用x表示,共分成四组:A. ,B.
,B. ,C.
,C. ,D.
,D. ),下面给出了部分信息:
),下面给出了部分信息:
七年级10名学生的竞赛成绩是:96,84,97,85,96,96,96,84,90,96.
八年级10名学生的竞赛成绩在C组中的数据是:92,92,94,94.
七、八年级抽取的学生竞赛成绩统计表
八年级抽取的学生竞赛成绩扇形统计图

根据以上信息,解答下列问题:
(1)上述图表中 __________,
__________, __________,
__________, __________;
__________;
(2)根据以上数据,你认为该校七、八年级中哪个年级学生掌握防溺水安全知识较好?请说明理由(一条理由即可);
(3)该校七、八年级共1200人参加了此次竞赛活动,估计参加此次竞赛活动成绩优秀( )的学生人数是多少?
)的学生人数是多少?
 ,B.
,B. ,C.
,C. ,D.
,D. ),下面给出了部分信息:
),下面给出了部分信息:七年级10名学生的竞赛成绩是:96,84,97,85,96,96,96,84,90,96.
八年级10名学生的竞赛成绩在C组中的数据是:92,92,94,94.
七、八年级抽取的学生竞赛成绩统计表
| 年级 | 七年级 | 八年级 |
| 平均数 | 92 | 92 |
| 中位数 | 96 | m |
| 众数 | b | 98 |
| 方差 | 28.6 | 28 |

根据以上信息,解答下列问题:
(1)上述图表中
 __________,
__________, __________,
__________, __________;
__________;(2)根据以上数据,你认为该校七、八年级中哪个年级学生掌握防溺水安全知识较好?请说明理由(一条理由即可);
(3)该校七、八年级共1200人参加了此次竞赛活动,估计参加此次竞赛活动成绩优秀(
 )的学生人数是多少?
)的学生人数是多少?20.某老年活动中心欲在一房前3m高的前墙( )上安装一遮阳篷
)上安装一遮阳篷 ,使正午时刻房前能有2m宽的阴影处(
,使正午时刻房前能有2m宽的阴影处( )以供纳凉,假设此地某日正午时刻太阳光与水平地面的夹角为63.4°,遮阳篷
)以供纳凉,假设此地某日正午时刻太阳光与水平地面的夹角为63.4°,遮阳篷 与水平面的夹角为10°,如图为侧面示意图,请你求出此遮阳篷
与水平面的夹角为10°,如图为侧面示意图,请你求出此遮阳篷 的长度(结果精确到0.1m).(参考数据:
的长度(结果精确到0.1m).(参考数据: ,
, ,
, ;
; ,
, ,
, )
)

 )上安装一遮阳篷
)上安装一遮阳篷 ,使正午时刻房前能有2m宽的阴影处(
,使正午时刻房前能有2m宽的阴影处( )以供纳凉,假设此地某日正午时刻太阳光与水平地面的夹角为63.4°,遮阳篷
)以供纳凉,假设此地某日正午时刻太阳光与水平地面的夹角为63.4°,遮阳篷 与水平面的夹角为10°,如图为侧面示意图,请你求出此遮阳篷
与水平面的夹角为10°,如图为侧面示意图,请你求出此遮阳篷 的长度(结果精确到0.1m).(参考数据:
的长度(结果精确到0.1m).(参考数据: ,
, ,
, ;
; ,
, ,
, )
)
21.某商场进货员预测一种应季T恤衫能畅销市场,就用4000元购进一批这种T恤衫,面市后果然供不应求.商场又用8800元购进了第二批这种T恤衫,所购数量是第一批购进量的2倍,但每件的进价贵了4元.
(1)该商场购进第一批、第二批T恤衫每件的进价分别是多少元?
(2)如果两批T恤衫按相同的标价销售,最后缺码的40件T恤衫按七折优惠售出,要使两批T恤衫全部售完后利润率不低于80%(不考虑其他因素),那么每件T恤衫的标价至少是多少元?
(1)该商场购进第一批、第二批T恤衫每件的进价分别是多少元?
(2)如果两批T恤衫按相同的标价销售,最后缺码的40件T恤衫按七折优惠售出,要使两批T恤衫全部售完后利润率不低于80%(不考虑其他因素),那么每件T恤衫的标价至少是多少元?
22.如图,一次函数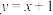 与反比例函数
与反比例函数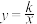 的图象相交于
的图象相交于 ,B两点,分别连接
,B两点,分别连接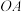 ,
, .
.

(1)求这个反比例函数的表达式;
(2)求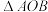 的面积;
的面积;
(3)在平面内是否存在一点P,使以点O,B,A,P为顶点的四边形为平行四边形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
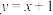 与反比例函数
与反比例函数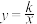 的图象相交于
的图象相交于 ,B两点,分别连接
,B两点,分别连接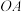 ,
, .
.
(1)求这个反比例函数的表达式;
(2)求
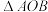 的面积;
的面积;(3)在平面内是否存在一点P,使以点O,B,A,P为顶点的四边形为平行四边形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
23.如图,在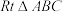 中,
中, ,点O为
,点O为 边上一点,以
边上一点,以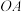 为半径的⊙
为半径的⊙ 与
与 相切于点D,分别交
相切于点D,分别交 ,
, 边于点E,F.
边于点E,F.

(1)求证: 平分
平分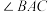 ;
;
(2)若 ,
, ,求⊙
,求⊙ 的半径.
的半径.
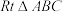 中,
中, ,点O为
,点O为 边上一点,以
边上一点,以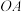 为半径的⊙
为半径的⊙ 与
与 相切于点D,分别交
相切于点D,分别交 ,
, 边于点E,F.
边于点E,F.
(1)求证:
 平分
平分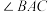 ;
;(2)若
 ,
, ,求⊙
,求⊙ 的半径.
的半径.24.某校一数学兴趣小组在一次合作探究活动中,将两块大小不同的等腰直角三角形 和等腰直角三角形
和等腰直角三角形 ,按如图1的方式摆放,
,按如图1的方式摆放, ,随后保持
,随后保持 不动,将
不动,将 绕点C按逆时针方向旋转
绕点C按逆时针方向旋转 (
( ),连接
),连接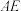 ,
, ,延长
,延长 交
交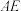 于点F,连接
于点F,连接 .该数学兴趣小组进行如下探究,请你帮忙解答:
.该数学兴趣小组进行如下探究,请你帮忙解答:


(1)【初步探究】如图2,当 时,则
时,则 _____;
_____;
(2)【初步探究】如图3,当点E,F重合时,请直接写出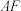 ,
,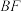 ,
, 之间的数量关系:_________;
之间的数量关系:_________;
(3)【深入探究】如图4,当点E,F不重合时,(2)中的结论是否仍然成立?若成立,请给出推理过程;若不成立,请说明理由.
(4)【拓展延伸】如图5,在 与
与 中,
中, ,若
,若 ,
, (m为常数).保持
(m为常数).保持 不动,将
不动,将 绕点C按逆时针方向旋转
绕点C按逆时针方向旋转 (
( ),连接
),连接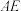 ,
, ,延长
,延长 交
交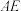 于点F,连接
于点F,连接 ,如图6.试探究
,如图6.试探究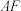 ,
,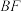 ,
, 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
 和等腰直角三角形
和等腰直角三角形 ,按如图1的方式摆放,
,按如图1的方式摆放, ,随后保持
,随后保持 不动,将
不动,将 绕点C按逆时针方向旋转
绕点C按逆时针方向旋转 (
( ),连接
),连接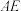 ,
, ,延长
,延长 交
交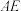 于点F,连接
于点F,连接 .该数学兴趣小组进行如下探究,请你帮忙解答:
.该数学兴趣小组进行如下探究,请你帮忙解答:

(1)【初步探究】如图2,当
 时,则
时,则 _____;
_____;(2)【初步探究】如图3,当点E,F重合时,请直接写出
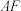 ,
,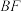 ,
, 之间的数量关系:_________;
之间的数量关系:_________;(3)【深入探究】如图4,当点E,F不重合时,(2)中的结论是否仍然成立?若成立,请给出推理过程;若不成立,请说明理由.
(4)【拓展延伸】如图5,在
 与
与 中,
中, ,若
,若 ,
, (m为常数).保持
(m为常数).保持 不动,将
不动,将 绕点C按逆时针方向旋转
绕点C按逆时针方向旋转 (
( ),连接
),连接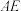 ,
, ,延长
,延长 交
交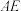 于点F,连接
于点F,连接 ,如图6.试探究
,如图6.试探究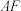 ,
,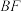 ,
, 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.25.如图1,在平面直角坐标系中,已知二次函数 的图象经过点
的图象经过点 ,
, ,与y轴交于点C.
,与y轴交于点C.

(1)求该二次函数的表达式;
(2)连接 ,在该二次函数图象上是否存在点P,使
,在该二次函数图象上是否存在点P,使 ?若存在,请求出点P的坐标:若不存在,请说明理由;
?若存在,请求出点P的坐标:若不存在,请说明理由;
(3)如图2,直线l为该二次函数图象的对称轴,交x轴于点E.若点Q为x轴上方二次函数图象上一动点,过点Q作直线 ,
, 分别交直线l于点M,N,在点Q的运动过程中,
分别交直线l于点M,N,在点Q的运动过程中, 的值是否为定值?若是,请求出该定值;若不是,请说明理由.
的值是否为定值?若是,请求出该定值;若不是,请说明理由.
 的图象经过点
的图象经过点 ,
, ,与y轴交于点C.
,与y轴交于点C.
(1)求该二次函数的表达式;
(2)连接
 ,在该二次函数图象上是否存在点P,使
,在该二次函数图象上是否存在点P,使 ?若存在,请求出点P的坐标:若不存在,请说明理由;
?若存在,请求出点P的坐标:若不存在,请说明理由;(3)如图2,直线l为该二次函数图象的对称轴,交x轴于点E.若点Q为x轴上方二次函数图象上一动点,过点Q作直线
 ,
, 分别交直线l于点M,N,在点Q的运动过程中,
分别交直线l于点M,N,在点Q的运动过程中, 的值是否为定值?若是,请求出该定值;若不是,请说明理由.
的值是否为定值?若是,请求出该定值;若不是,请说明理由. 搜索
搜索
 难度系数:0.85
难度系数:0.85  答案解析
答案解析
 有奖纠错
有奖纠错
