全一卷
1.实数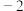 ,0,
,0, ,2中,为负数的是( )
,2中,为负数的是( )
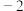 ,0,
,0, ,2中,为负数的是( )
,2中,为负数的是( )A.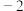 | B.0 | C. | D.2 |
2.截至2021年12月31日,全国共有共青团组织约367.7万个.将367.7万用科学记数法表示为( )
A. | B. | C. | D. |
3.下列英文字母为轴对称图形的是( )
| A.W | B.L | C.S | D.Q |
4.下列运算中,正确的是( )
A. | B. |
C. | D. |
5.下列立体图形中,俯视图是三角形的是( )
A. | B. | C. | D. |
6.中考体育测试,某组10名男生引体向上个数分别为:6,8,8,7,7,8,9,7,8,9.则这组数据的中位数和众数分别是( )
| A.7.5,7 | B.7.5,8 | C.8,7 | D.8,8 |
7.在 中,
中, ,
, ,
, ,点
,点 ,
, ,
, 分别为边
分别为边 ,
, ,
, 的中点,则
的中点,则 的周长为( )
的周长为( )
 中,
中, ,
, ,
, ,点
,点 ,
, ,
, 分别为边
分别为边 ,
, ,
, 的中点,则
的中点,则 的周长为( )
的周长为( )| A.9 | B.12 | C.14 | D.16 |
8.化简 的结果是( )
的结果是( )
 的结果是( )
的结果是( )| A.1 | B. | C. | D. |
9.我国古代数学名著《九章算术》记载:“今有牛五、羊二,直金十九两;牛二、羊三,直金十二两.问牛、羊各直金几何?”题目大意是:5头牛、2只羊共19两银子;2头牛、3只羊共12两银子,每头牛、每只羊各多少两银子?设1头牛 两银子,1只羊
两银子,1只羊 两银子,则可列方程组为( )
两银子,则可列方程组为( )
 两银子,1只羊
两银子,1只羊 两银子,则可列方程组为( )
两银子,则可列方程组为( )A. | B. | C. | D. |
10.如图是不倒翁的主视图,不倒翁的圆形脸恰好与帽子边沿 ,
, 分别相切于点
分别相切于点 ,
, ,不倒翁的鼻尖正好是圆心
,不倒翁的鼻尖正好是圆心 ,若
,若 ,则
,则 的度数为( )
的度数为( )

 ,
, 分别相切于点
分别相切于点 ,
, ,不倒翁的鼻尖正好是圆心
,不倒翁的鼻尖正好是圆心 ,若
,若 ,则
,则 的度数为( )
的度数为( )
A. | B. | C. | D. |
11.一次函数 的值随
的值随 的增大而增大,则点
的增大而增大,则点 所在象限为( )
所在象限为( )
 的值随
的值随 的增大而增大,则点
的增大而增大,则点 所在象限为( )
所在象限为( )| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
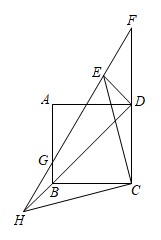
12.如图,四边形 为正方形,将
为正方形,将 绕点
绕点 逆时针旋转
逆时针旋转 至
至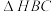 ,点
,点 ,
, ,
, 在同一直线上,
在同一直线上,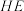 与
与 交于点
交于点 ,延长
,延长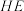 与
与 的延长线交于点
的延长线交于点 ,
,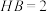 ,
,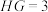 .以下结论:
.以下结论:
①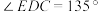 ;②
;② ;③
;③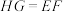 ;④
;④ .其中正确结论的个数为( )
.其中正确结论的个数为( )
 为正方形,将
为正方形,将 绕点
绕点 逆时针旋转
逆时针旋转 至
至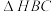 ,点
,点 ,
, ,
, 在同一直线上,
在同一直线上,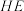 与
与 交于点
交于点 ,延长
,延长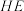 与
与 的延长线交于点
的延长线交于点 ,
,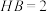 ,
,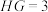 .以下结论:
.以下结论:①
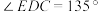 ;②
;② ;③
;③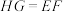 ;④
;④ .其中正确结论的个数为( )
.其中正确结论的个数为( )
| A.1个 | B.2个 | C.3个 | D.4个 |
13.分解因式:
________ .

14.如图,已知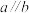 ,
,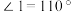 ,则
,则 的度数为
的度数为________ .

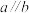 ,
,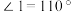 ,则
,则 的度数为
的度数为
15.一个多边形外角和是内角和的 ,则这个多边形的边数为
,则这个多边形的边数为________ .
 ,则这个多边形的边数为
,则这个多边形的边数为16.设 ,
, 是方程
是方程 的两个实数根,则
的两个实数根,则 的值为
的值为________ .
 ,
, 是方程
是方程 的两个实数根,则
的两个实数根,则 的值为
的值为17.将一组数 ,2,
,2, ,
, ,…,
,…, ,按下列方式进行排列:
,按下列方式进行排列:
 ,2,
,2, ,
, ;
;
 ,
, ,
, ,4;
,4;
…
若2的位置记为 ,
, 的位置记为
的位置记为 ,则
,则 的位置记为
的位置记为________ .
 ,2,
,2, ,
, ,…,
,…, ,按下列方式进行排列:
,按下列方式进行排列: ,2,
,2, ,
, ;
; ,
, ,
, ,4;
,4;…
若2的位置记为
 ,
, 的位置记为
的位置记为 ,则
,则 的位置记为
的位置记为18.如图,点 为矩形
为矩形 的对角线
的对角线 上一动点,点
上一动点,点 为
为 的中点,连接
的中点,连接 ,
, ,若
,若 ,
, ,则
,则 的最小值为
的最小值为________ .

 为矩形
为矩形 的对角线
的对角线 上一动点,点
上一动点,点 为
为 的中点,连接
的中点,连接 ,
, ,若
,若 ,
, ,则
,则 的最小值为
的最小值为
19.计算: .
.
 .
.20.解方程: .
.
 .
.21.北京冬奥组委会对志愿者开展培训活动,为了解某批次培训活动效果,随机抽取了20名志愿者的测试成绩.成绩如下:
84 93 91 87 94 86 97 100 88 94
92 91 82 89 87 92 98 92 93 88
整理上面的数据,得到频数分布表和扇形统计图:
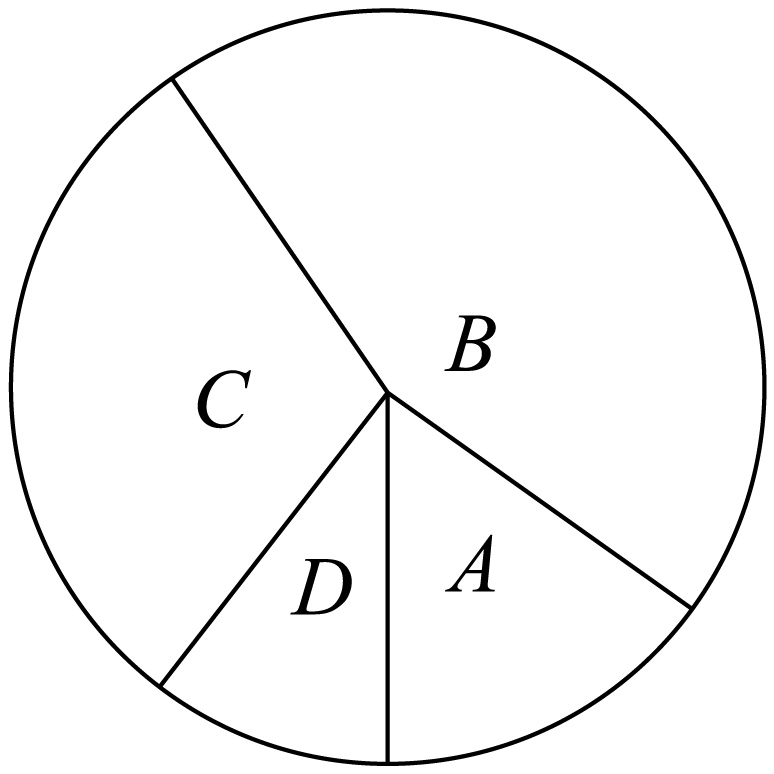
请根据以上信息,解答下列问题:
(1) 等级的频数为________,
等级的频数为________, 所对应的扇形圆心角度数为________;
所对应的扇形圆心角度数为________;
(2)该批志愿者有1500名,若成绩不低于90分为优秀,请估计这批志愿者中成绩达到优秀等级的人数;
(3)已知 等级中有2名男志愿者,现从
等级中有2名男志愿者,现从 等级中随机抽取2名志愿者,试用列表或画树状图的方法求出恰好抽到一男一女的概率.
等级中随机抽取2名志愿者,试用列表或画树状图的方法求出恰好抽到一男一女的概率.
84 93 91 87 94 86 97 100 88 94
92 91 82 89 87 92 98 92 93 88
整理上面的数据,得到频数分布表和扇形统计图:
| 等级 | 成绩/分 | 频数 |
 |  | 3 |
 |  | 9 |
 |  | ▲ |
 |  | 2 |

请根据以上信息,解答下列问题:
(1)
 等级的频数为________,
等级的频数为________, 所对应的扇形圆心角度数为________;
所对应的扇形圆心角度数为________;(2)该批志愿者有1500名,若成绩不低于90分为优秀,请估计这批志愿者中成绩达到优秀等级的人数;
(3)已知
 等级中有2名男志愿者,现从
等级中有2名男志愿者,现从 等级中随机抽取2名志愿者,试用列表或画树状图的方法求出恰好抽到一男一女的概率.
等级中随机抽取2名志愿者,试用列表或画树状图的方法求出恰好抽到一男一女的概率.22.数学实践活动小组去测量眉山市某标志性建筑物的高 .如图,在楼前平地
.如图,在楼前平地 处测得楼顶
处测得楼顶 处的仰角为
处的仰角为 ,沿
,沿 方向前进
方向前进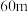 到达
到达 处,测得楼顶
处,测得楼顶 处的仰角为
处的仰角为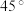 ,求此建筑物的高.(结果保留整数.参考数据:
,求此建筑物的高.(结果保留整数.参考数据: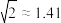 ,
,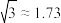 )
)
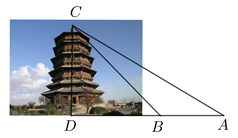
 .如图,在楼前平地
.如图,在楼前平地 处测得楼顶
处测得楼顶 处的仰角为
处的仰角为 ,沿
,沿 方向前进
方向前进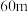 到达
到达 处,测得楼顶
处,测得楼顶 处的仰角为
处的仰角为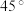 ,求此建筑物的高.(结果保留整数.参考数据:
,求此建筑物的高.(结果保留整数.参考数据: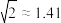 ,
,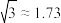 )
)
23.已知直线 与反比例函数
与反比例函数 的图象在第一象限交于点
的图象在第一象限交于点 .
.

(1)求反比例函数的解析式;
(2)如图,将直线 向上平移
向上平移 个单位后与
个单位后与 的图象交于点
的图象交于点 和点
和点 ,求
,求 的值;
的值;
(3)在(2)的条件下,设直线 与
与 轴、
轴、 轴分别交于点
轴分别交于点 ,
, ,求证:
,求证: .
.
 与反比例函数
与反比例函数 的图象在第一象限交于点
的图象在第一象限交于点 .
.
(1)求反比例函数的解析式;
(2)如图,将直线
 向上平移
向上平移 个单位后与
个单位后与 的图象交于点
的图象交于点 和点
和点 ,求
,求 的值;
的值;(3)在(2)的条件下,设直线
 与
与 轴、
轴、 轴分别交于点
轴分别交于点 ,
, ,求证:
,求证: .
.24.建设美丽城市,改造老旧小区.某市2019年投入资金1000万元,2021年投入资金1440万元,现假定每年投入资金的增长率相同.
(1)求该市改造老旧小区投入资金的年平均增长率;
(2)2021年老旧小区改造的平均费用为每个80万元.2022年为提高老旧小区品质,每个小区改造费用增加15%.如果投入资金年增长率保持不变,求该市在2022年最多可以改造多少个老旧小区?
(1)求该市改造老旧小区投入资金的年平均增长率;
(2)2021年老旧小区改造的平均费用为每个80万元.2022年为提高老旧小区品质,每个小区改造费用增加15%.如果投入资金年增长率保持不变,求该市在2022年最多可以改造多少个老旧小区?
25.如图, 为
为 的直径,点
的直径,点 是
是 上一点,
上一点, 与
与 相切于点
相切于点 ,过点
,过点 作
作 ,连接
,连接 ,
, .
.

(1)求证: 是
是 的角平分线;
的角平分线;
(2)若 ,
, ,求
,求 的长;
的长;
(3)在(2)的条件下,求阴影部分的面积.
 为
为 的直径,点
的直径,点 是
是 上一点,
上一点, 与
与 相切于点
相切于点 ,过点
,过点 作
作 ,连接
,连接 ,
, .
.
(1)求证:
 是
是 的角平分线;
的角平分线;(2)若
 ,
, ,求
,求 的长;
的长;(3)在(2)的条件下,求阴影部分的面积.
26.在平面直角坐标系中,抛物线 与
与 轴交于点
轴交于点 ,
, (点
(点 在点
在点 的左侧),与
的左侧),与 轴交于点
轴交于点 ,且点
,且点 的坐标为
的坐标为 .
.

(1)求点 的坐标;
的坐标;
(2)如图1,若点 是第二象限内抛物线上一动点,求点
是第二象限内抛物线上一动点,求点 到直线
到直线 距离的最大值;
距离的最大值;
(3)如图2,若点 是抛物线上一点,点
是抛物线上一点,点 是抛物线对称轴上一点,是否存在点
是抛物线对称轴上一点,是否存在点 使以
使以 ,
, ,
, ,
, 为顶点的四边形是平行四边形?若存在,请直接写出点
为顶点的四边形是平行四边形?若存在,请直接写出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
 与
与 轴交于点
轴交于点 ,
, (点
(点 在点
在点 的左侧),与
的左侧),与 轴交于点
轴交于点 ,且点
,且点 的坐标为
的坐标为 .
.
(1)求点
 的坐标;
的坐标;(2)如图1,若点
 是第二象限内抛物线上一动点,求点
是第二象限内抛物线上一动点,求点 到直线
到直线 距离的最大值;
距离的最大值;(3)如图2,若点
 是抛物线上一点,点
是抛物线上一点,点 是抛物线对称轴上一点,是否存在点
是抛物线对称轴上一点,是否存在点 使以
使以 ,
, ,
, ,
, 为顶点的四边形是平行四边形?若存在,请直接写出点
为顶点的四边形是平行四边形?若存在,请直接写出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由. 搜索
搜索
 难度系数:0.94
难度系数:0.94  答案解析
答案解析
 有奖纠错
有奖纠错
