全一卷
1.-2的绝对值是( )
| A.2 | B. | C. | D. |
2.下列运算正确的是( )
A. | B. |
C. | D. |
3.如图,AB∥ED,若∠1=70°,则∠2的度数是( )


| A.70° | B.80° | C.100° | D.110° |
4.下列展开图中,是正方体展开图的是( )
A. | B. |
C. | D. |
5.若等腰三角形的两边长分别是3cm和5cm,则这个等腰三角形的周长是( )
| A.8cm | B.13cm | C.8cm或13cm | D.11cm或13cm |
6.我国古代《算法统宗》里有这样一首诗:“我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空.”诗中后面两句的意思是:如果一间客房住7人,那么有7人无房可住;如果一间客房住9人,那么就空出一间客房,若设该店有客房x间,房客y人,则列出关于x、y的二元一次方程组正确的是( )
A. | B. | C. | D. |
7.如果 ,那么下列不等式正确的是( )
,那么下列不等式正确的是( )
 ,那么下列不等式正确的是( )
,那么下列不等式正确的是( )A. | B. | C. | D. |
8.如图,点A在反比例函数 的图像上,以
的图像上,以 为一边作等腰直角三角形
为一边作等腰直角三角形 ,其中∠
,其中∠ =90°,
=90°, ,则线段
,则线段 长的最小值是( )
长的最小值是( )

 的图像上,以
的图像上,以 为一边作等腰直角三角形
为一边作等腰直角三角形 ,其中∠
,其中∠ =90°,
=90°, ,则线段
,则线段 长的最小值是( )
长的最小值是( )
| A.1 | B. | C. | D.4 |
9.分解因式:3a2﹣12=___ .
10.2022年5月,国家林业和草原局湿地管理司在第二季度侧行发布会上表示,到“十四五”末,我国力争将湿地保护率提高到55%,其中修复红树林146200亩,请将146200用科学记数法表示是____ .
11.已知一组数据:4,5,5,6,5,4,7,8,则这组数据的众数是___ .
12.满足 的最大整数
的最大整数 是
是_______ .
 的最大整数
的最大整数 是
是13.若关于 的一元二次方程
的一元二次方程 有实数根,则实数k的取值范围是
有实数根,则实数k的取值范围是_____ .
 的一元二次方程
的一元二次方程 有实数根,则实数k的取值范围是
有实数根,则实数k的取值范围是14.将半径为6cm,圆心角是120°的扇形围成一个圆锥的侧面,则这个圆锥底面圆的半径为______ cm.
15.按规律排列的单项式: ,
, ,
,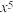 ,
, ,
,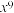 ,…,则第20个单项式是
,…,则第20个单项式是_____ .
 ,
, ,
,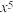 ,
, ,
,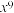 ,…,则第20个单项式是
,…,则第20个单项式是16.甲、乙两位同学各给出某函数的一个特征,甲:“函数值y随自变量x增大而减小”;乙:“函数图像经过点(0,2)”,请你写出一个同时满足这两个特征的函数,其表达式是____ .
17.如图,在正六边形ABCDEF中,AB=6,点M在边AF上,且AM=2.若经过点M的直线l将正六边形面积平分,则直线l被正六边形所截的线段长是_____ .


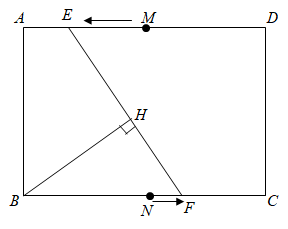
18.如图,在矩形 中,
中, =6,
=6, =8,点
=8,点 、
、 分别是边
分别是边 、
、 的中点,某一时刻,动点
的中点,某一时刻,动点 从点
从点 出发,沿
出发,沿 方向以每秒2个单位长度的速度向点
方向以每秒2个单位长度的速度向点 匀速运动;同时,动点
匀速运动;同时,动点 从点
从点 出发,沿
出发,沿 方向以每秒1个单位长度的速度向点
方向以每秒1个单位长度的速度向点 匀速运动,其中一点运动到矩形顶点时,两点同时停止运动,连接
匀速运动,其中一点运动到矩形顶点时,两点同时停止运动,连接 ,过点
,过点 作
作 的垂线,垂足为
的垂线,垂足为 .在这一运动过程中,点
.在这一运动过程中,点 所经过的路径长是
所经过的路径长是_____ .
 中,
中, =6,
=6, =8,点
=8,点 、
、 分别是边
分别是边 、
、 的中点,某一时刻,动点
的中点,某一时刻,动点 从点
从点 出发,沿
出发,沿 方向以每秒2个单位长度的速度向点
方向以每秒2个单位长度的速度向点 匀速运动;同时,动点
匀速运动;同时,动点 从点
从点 出发,沿
出发,沿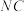 方向以每秒1个单位长度的速度向点
方向以每秒1个单位长度的速度向点 匀速运动,其中一点运动到矩形顶点时,两点同时停止运动,连接
匀速运动,其中一点运动到矩形顶点时,两点同时停止运动,连接 ,过点
,过点 作
作 的垂线,垂足为
的垂线,垂足为 .在这一运动过程中,点
.在这一运动过程中,点 所经过的路径长是
所经过的路径长是
19.计算: 4
4 °.
°.
 4
4 °.
°.20.解方程: .
.
 .
.21.如图,在平行四边形 中,点
中,点 ,
, 分别是边
分别是边 ,
, 的中点.求证:
的中点.求证: .
.
 中,点
中,点 ,
, 分别是边
分别是边 ,
, 的中点.求证:
的中点.求证: .
.
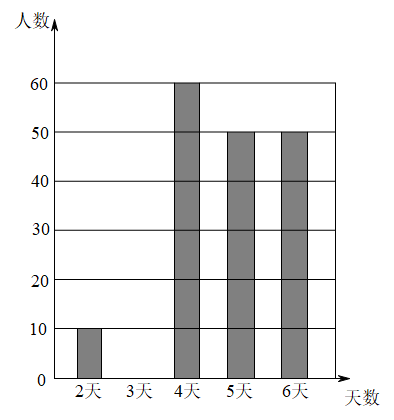
22.为了解某校九年级学生开展“综合与实践”活动的情况,抽样调查了该校 名九年级学生上学期参加“综合与实践”活动的天数,并根据调查所得的数据绘制了如下尚不完整的两幅统计图.根据图表信息,解答下列问题:
名九年级学生上学期参加“综合与实践”活动的天数,并根据调查所得的数据绘制了如下尚不完整的两幅统计图.根据图表信息,解答下列问题:

(1)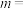 ,
, ;
;
(2)补全条形统计图;
(3)根据抽样调查的结果,请你估计该校九年级2000名学生中上学期参加“综合与实践”活动4天及以上的人数.
 名九年级学生上学期参加“综合与实践”活动的天数,并根据调查所得的数据绘制了如下尚不完整的两幅统计图.根据图表信息,解答下列问题:
名九年级学生上学期参加“综合与实践”活动的天数,并根据调查所得的数据绘制了如下尚不完整的两幅统计图.根据图表信息,解答下列问题:

(1)
 ,
, ;
;(2)补全条形统计图;
(3)根据抽样调查的结果,请你估计该校九年级2000名学生中上学期参加“综合与实践”活动4天及以上的人数.
23.从甲、乙、丙、丁4名学生中选2名学生参加一次乒乓球单打比赛,求下列事件发生的概率.
(1)甲一定参加比赛,再从其余3名学生中任意选取1名,恰好选中丙的概率是 ;
(2)任意选取2名学生参加比赛,求一定有乙的概率.(用树状图或列表的方法求解).
(1)甲一定参加比赛,再从其余3名学生中任意选取1名,恰好选中丙的概率是 ;
(2)任意选取2名学生参加比赛,求一定有乙的概率.(用树状图或列表的方法求解).
24.如图,某学习小组在教学楼 的顶部观测信号塔
的顶部观测信号塔 底部的俯角为30°,信号塔顶部的仰角为45°.已知教学楼
底部的俯角为30°,信号塔顶部的仰角为45°.已知教学楼 的高度为20m,求信号塔的高度(计算结果保留根号).
的高度为20m,求信号塔的高度(计算结果保留根号).

 的顶部观测信号塔
的顶部观测信号塔 底部的俯角为30°,信号塔顶部的仰角为45°.已知教学楼
底部的俯角为30°,信号塔顶部的仰角为45°.已知教学楼 的高度为20m,求信号塔的高度(计算结果保留根号).
的高度为20m,求信号塔的高度(计算结果保留根号).
25.如图,在
 中,∠
中,∠ =45°,
=45°, ,以
,以 为直径的⊙
为直径的⊙ 与边
与边 交于点
交于点 .
.
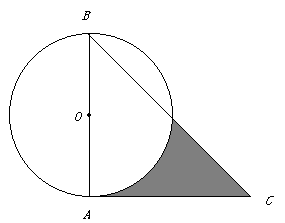
(1)判断直线 与⊙
与⊙ 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)若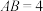 ,求图中阴影部分的面积.
,求图中阴影部分的面积.

 中,∠
中,∠ =45°,
=45°, ,以
,以 为直径的⊙
为直径的⊙ 与边
与边 交于点
交于点 .
.
(1)判断直线
 与⊙
与⊙ 的位置关系,并说明理由;
的位置关系,并说明理由;(2)若
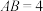 ,求图中阴影部分的面积.
,求图中阴影部分的面积.26.某单位准备购买文化用品,现有甲、乙两家超市进行促销活动,该文化用品两家超市的标价均为10元/件,甲超市一次性购买金额不超过400元的不优惠,超过400元的部分按标价的6折售卖;乙超市全部按标价的8折售卖.
(1)若该单位需要购买30件这种文化用品,则在甲超市的购物金额为 元;乙超市的购物金额为 元;
(2)假如你是该单位的采购员,你认为选择哪家超市支付的费用较少?
(1)若该单位需要购买30件这种文化用品,则在甲超市的购物金额为 元;乙超市的购物金额为 元;
(2)假如你是该单位的采购员,你认为选择哪家超市支付的费用较少?
27.如图,在网格中,每个小正方形的边长均为1,每个小正方形的顶点称为格点,点 、
、 、
、 、
、 、
、 均为格点.
均为格点.
【操作探究】在数学活动课上,佳佳同学在如图①的网格中,用无刻度的直尺画了两条互相垂直的线段 、
、 ,相交于点
,相交于点 并给出部分说理过程,请你补充完整:
并给出部分说理过程,请你补充完整:
解:在网格中取格点 ,构建两个直角三角形,分别是△ABC和△CDE.
,构建两个直角三角形,分别是△ABC和△CDE.
在Rt△ABC中,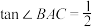
在Rt△CDE中, ,
所以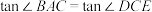 .
.
所以∠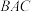 =∠
=∠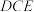 .
.
因为∠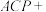 ∠
∠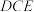 =∠
=∠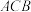 =90°,
=90°,
所以∠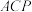 +∠
+∠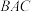 =90°,
=90°,
所以∠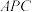 =90°,
=90°,
即 ⊥
⊥ .
.
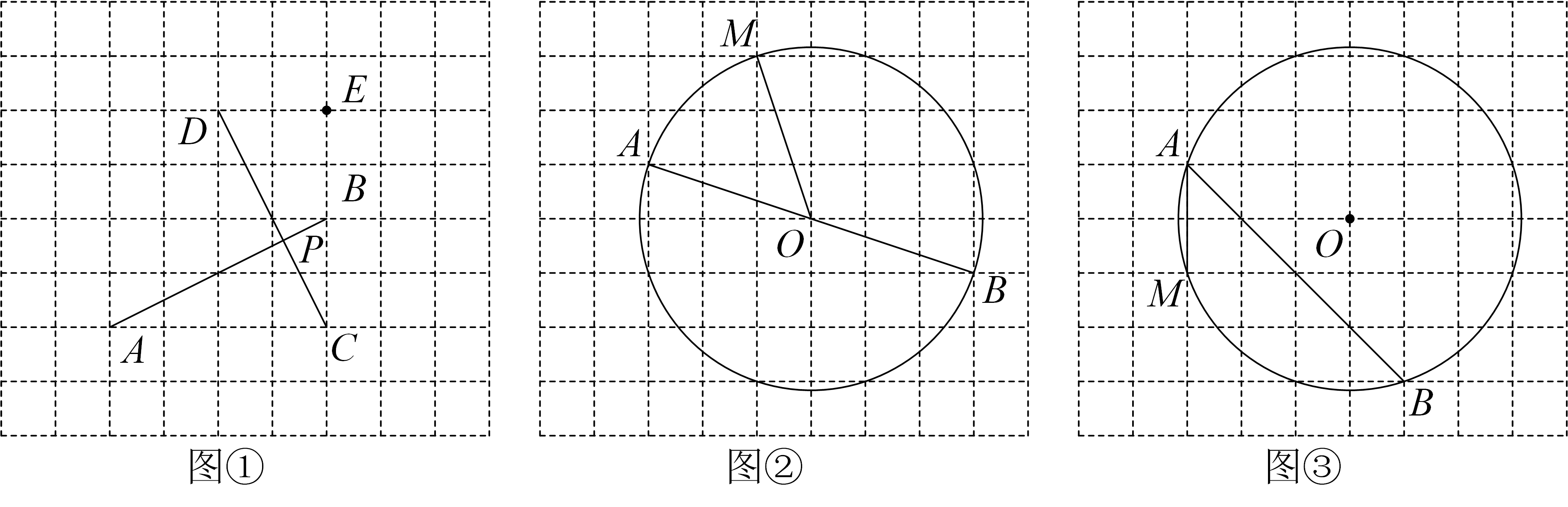
(1)【拓展应用】如图②是以格点 为圆心,
为圆心, 为直径的圆,请你只用无刻度的直尺,在
为直径的圆,请你只用无刻度的直尺,在 上找出一点P,使
上找出一点P,使 =
= ,写出作法,并给出证明:
,写出作法,并给出证明:
(2)【拓展应用】如图③是以格点 为圆心的圆,请你只用无刻度的直尺,在弦
为圆心的圆,请你只用无刻度的直尺,在弦 上找出一点P.使
上找出一点P.使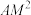 =
= ·
· ,写出作法,不用证明.
,写出作法,不用证明.
 、
、 、
、 、
、 、
、 均为格点.
均为格点.【操作探究】在数学活动课上,佳佳同学在如图①的网格中,用无刻度的直尺画了两条互相垂直的线段
 、
、 ,相交于点
,相交于点 并给出部分说理过程,请你补充完整:
并给出部分说理过程,请你补充完整:解:在网格中取格点
 ,构建两个直角三角形,分别是△ABC和△CDE.
,构建两个直角三角形,分别是△ABC和△CDE.在Rt△ABC中,
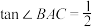
在Rt△CDE中, ,
所以
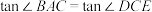 .
.所以∠
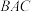 =∠
=∠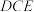 .
.因为∠
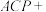 ∠
∠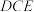 =∠
=∠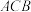 =90°,
=90°,所以∠
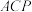 +∠
+∠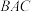 =90°,
=90°,所以∠
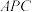 =90°,
=90°,即
 ⊥
⊥ .
.
(1)【拓展应用】如图②是以格点
 为圆心,
为圆心, 为直径的圆,请你只用无刻度的直尺,在
为直径的圆,请你只用无刻度的直尺,在 上找出一点P,使
上找出一点P,使 =
= ,写出作法,并给出证明:
,写出作法,并给出证明:(2)【拓展应用】如图③是以格点
 为圆心的圆,请你只用无刻度的直尺,在弦
为圆心的圆,请你只用无刻度的直尺,在弦 上找出一点P.使
上找出一点P.使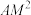 =
= ·
· ,写出作法,不用证明.
,写出作法,不用证明.28.如图,二次函数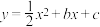 与
与 轴交于
轴交于 (0,0),
(0,0), (4,0)两点,顶点为
(4,0)两点,顶点为 ,连接
,连接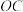 、
、 ,若点
,若点 是线段
是线段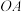 上一动点,连接
上一动点,连接 ,将
,将 沿
沿 折叠后,点
折叠后,点 落在点
落在点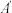 的位置,线段
的位置,线段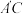 与
与 轴交于点
轴交于点 ,且点
,且点 与
与 、
、 点不重合.
点不重合.
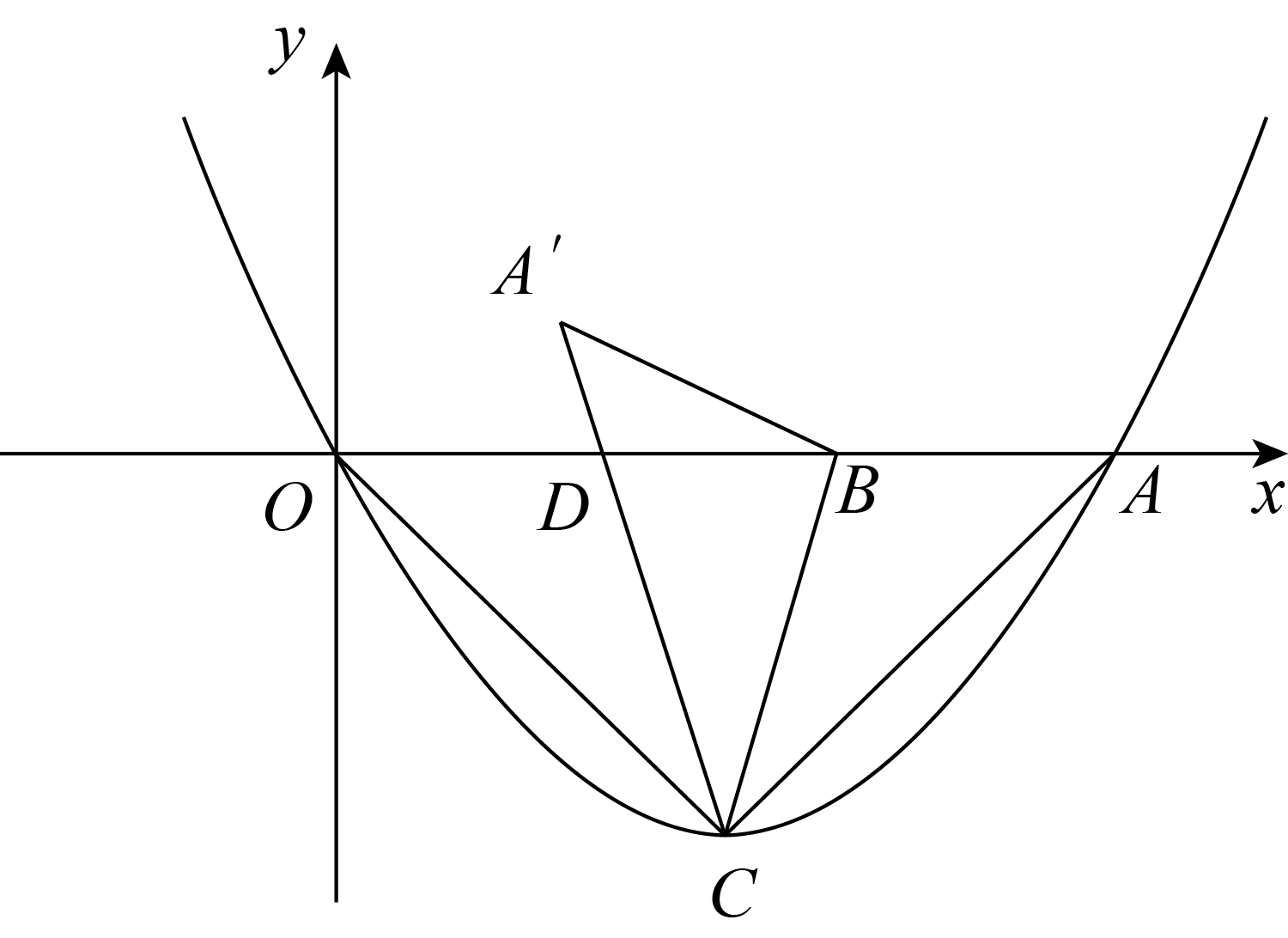
(1)求二次函数的表达式;
(2)①求证: ;
;
②求 ;
;
(3)当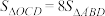 时,求直线
时,求直线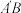 与二次函数的交点横坐标.
与二次函数的交点横坐标.
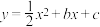 与
与 轴交于
轴交于 (0,0),
(0,0), (4,0)两点,顶点为
(4,0)两点,顶点为 ,连接
,连接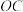 、
、 ,若点
,若点 是线段
是线段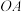 上一动点,连接
上一动点,连接 ,将
,将 沿
沿 折叠后,点
折叠后,点 落在点
落在点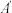 的位置,线段
的位置,线段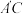 与
与 轴交于点
轴交于点 ,且点
,且点 与
与 、
、 点不重合.
点不重合.
(1)求二次函数的表达式;
(2)①求证:
 ;
;②求
 ;
;(3)当
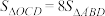 时,求直线
时,求直线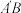 与二次函数的交点横坐标.
与二次函数的交点横坐标. 搜索
搜索
 难度系数:0.94
难度系数:0.94  答案解析
答案解析
 有奖纠错
有奖纠错
