搜索
全一卷
难度系数：0.85 
答案解析
有奖纠错
1．
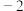的倒数是（ ）
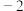的倒数是（ ）| A．2 | B． | C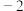． | D． |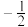
2．下面图形中既是轴对称图形又是中心对称图形的是（ ）
| A．科克曲线 | B．笛卡尔心形线 | C．阿基米德螺旋线 | D．赵爽弦图 |
3．2022年4月16日，神舟十三号飞船脱离天宫空间站后成功返回地面，总共飞行里程约198000公里．数据198000用科学记数法表示为（ ）
A． | B． | C． | D． |
4．如图是正方体的一种展开图，那么在原正方体中与“我”字所在面相对的面上的汉字是（ ）
| A．大 | B．美 | C．遂 | D．宁 |
5．下列计算中正确的是（ ）
A． | B． |
C． | D． |
6．若关于x的方程
无解，则m的值为（ ）
无解，则m的值为（ ）| A．0 | B．4或6 | C．6 | D．0或4 |
7．如图，圆锥底面圆半径为7cm，高为24cm，则它侧面展开图的面积是（ ）
A． cm2 | B． cm2 | C． cm2 | D． cm2 |
8．如图，D、E、F分别是
三边上的点，其中
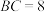，BC边上的高为6，且DE//BC，则
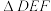面积的最大值为（ ）
三边上的点，其中
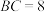，BC边上的高为6，且DE//BC，则
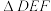面积的最大值为（ ）
| A．6 | B．8 | C．10 | D．12 |
9．已知m为方程
的根，那么
的值为（ ）
的根，那么的值为（ ）A． | B．0 | C．2022 | D．4044 |
10．如图，正方形ABCD与正方形BEFG有公共顶点B，连接EC、GA，交于点O，GA与BC交于点P，连接OD、OB，则下列结论一定正确的是（ ）
①EC⊥AG；②△OBP∽△CAP；③OB平分∠CBG；④∠AOD=45°；
①EC⊥AG；②△OBP∽△CAP；③OB平分∠CBG；④∠AOD=45°；
| A．①③ | B．①②③ | C．②③ | D．①②④ |
11．遂宁市某星期周一到周五的平均气温数值为：22，24，20，23，25，这5个数的中位数是______ ．
12．实数a，b在数轴上的位置如图所示，化简
______ ．
13．如图，正六边形ABCDEF的顶点A、F分别在正方形BMGH的边BH、GH上．若正方形BMGH的边长为6，则正六边形ABCDEF的边长为______ ．
14．“勾股树”是以正方形一边为斜边向外作直角三角形，再以该直角三角形的两直角边分别向外作正方形，重复这一过程所画出来的图形，因为重复数次后的形状好似一棵树而得名．假设如图分别是第一代勾股树、第二代勾股树、第三代勾股树，按照勾股树的作图原理作图，则第六代勾股树中正方形的个数为______ ．
15．抛物线y=ax2+bx+c（a，b，c为常数）的部分图象如图所示，设m=a-b+c，则m的取值范围是______ ．
16．计算：
．
．17．先化简，再求值：
，其中
．
，其中．18．如图，在菱形ABCD中，对角线AC、BD相交于点O，点E是AD的中点，连接OE，过点D作DF∥AC交OE的延长线于点F，连接AF．
(1)求证：
≌
；
(2)判定四边形AODF的形状并说明理由．
(1)求证：
≌；(2)判定四边形AODF的形状并说明理由．
19．某中学为落实《教育部办公厅关于进一步加强中小学生体质管理的通知》文件要求，决定增设篮球、足球两门选修课程，需要购进一批篮球和足球．已知购买2个篮球和3个足球共需费用510元；购买3个篮球和5个足球共需费用810元．
(1)求篮球和足球的单价分别是多少元；
(2)学校计划采购篮球、足球共50个，并要求篮球不少于30个，且总费用不超过5500元．那么有哪几种购买方案？
(1)求篮球和足球的单价分别是多少元；
(2)学校计划采购篮球、足球共50个，并要求篮球不少于30个，且总费用不超过5500元．那么有哪几种购买方案？
20．北京冬奥会、冬残奥会的成功举办推动了我国冰雪运动的跨越式发展，激发了青少年对冰雪项目的浓厚兴趣．某校通过抽样调查的方法，对四个项目最感兴趣的人数进行了统计，含花样滑冰、短道速滑、自由式滑雪、单板滑雪四项（每人限选1项），制作了如下统计图（部分信息未给出）．
请你根据图中提供的信息解答下列问题：
(1)在这次调查中，一共调查了______名学生；若该校共有2000名学生，估计爱好花样滑冰运动的学生有______人；
(2)补全条形统计图；
(3)把短道速滑记为A、花样滑冰记为B、自由式滑雪记为C、单板滑雪记为D，学校将从这四个运动项目中抽出两项来做重点推介，请用画树状图或列表的方法求出抽到项目中恰有一项为自由式滑雪C的概率．
请你根据图中提供的信息解答下列问题：
(1)在这次调查中，一共调查了______名学生；若该校共有2000名学生，估计爱好花样滑冰运动的学生有______人；
(2)补全条形统计图；
(3)把短道速滑记为A、花样滑冰记为B、自由式滑雪记为C、单板滑雪记为D，学校将从这四个运动项目中抽出两项来做重点推介，请用画树状图或列表的方法求出抽到项目中恰有一项为自由式滑雪C的概率．
21．在平面直角坐标系中，如果一个点的横坐标与纵坐标互为相反数，则称该点为“黎点”．例如
，
都是“黎点”．
(1)求双曲线
上的“黎点”；
(2)若抛物线
（a、c为常数）上有且只有一个“黎点”，当
时，求c的取值范围．
，
都是“黎点”．(1)求双曲线
上的“黎点”；(2)若抛物线
（a、c为常数）上有且只有一个“黎点”，当
时，求c的取值范围．22．数学兴趣小组到一公园测量塔楼高度．如图所示，塔楼剖面和台阶的剖面在同一平面，在台阶底部点A处测得塔楼顶端点E的仰角
，台阶AB长26米，台阶坡面AB的坡度
，然后在点B处测得塔楼顶端点E的仰角
，则塔顶到地面的高度EF约为多少米．
（参考数据：
，
，
，
）
，台阶AB长26米，台阶坡面AB的坡度，然后在点B处测得塔楼顶端点E的仰角，则塔顶到地面的高度EF约为多少米．（参考数据：
，，，）23．已知一次函数
（a为常数）与x轴交于点A，与反比例函数
交于B、C两点，B点的横坐标为
．
(1)求出一次函数的解析式并在图中画出它的图象；
(2)求出点C的坐标，并根据图象写出当
时对应自变量x的取值范围；
(3)若点B与点D关于原点成中心对称，求出△ACD的面积．
（a为常数）与x轴交于点A，与反比例函数交于B、C两点，B点的横坐标为．(1)求出一次函数的解析式并在图中画出它的图象；
(2)求出点C的坐标，并根据图象写出当
时对应自变量x的取值范围；(3)若点B与点D关于原点成中心对称，求出△ACD的面积．
24．如图，
是
的外接圆，点O在BC上，
的角平分线交于点D，连接BD，CD，过点D作BC的平行线与AC的延长线相交于点P．
(1)求证：PD是的切线；
(2)求证：
∽
；
(3)若
，
，求点O到AD的距离．
是的外接圆，点O在BC上，的角平分线交于点D，连接BD，CD，过点D作BC的平行线与AC的延长线相交于点P．(1)求证：PD是
的切线；(2)求证：
∽；(3)若
，，求点O到AD的距离．25．如图，在平面直角坐标系中，抛物线
与x轴交于A、B两点，与y轴交于点C，其中点A的坐标为
，点C的坐标为
．
(1)求抛物线的解析式；
(2)如图1，E为边AB上的一动点，F为BC边上的一动点，D点坐标为
，求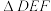周长的最小值；
(3)如图2，N为射线CB上的一点，M是抛物线上的一点，M、N均在第一象限内，B、N位于直线AM的同侧，若M到x轴的距离为d，
面积为
，当为等腰三角形时，求点N的坐标．
与x轴交于A、B两点，与y轴交于点C，其中点A的坐标为
，点C的坐标为
．
(1)求抛物线的解析式；
(2)如图1，E为
边AB上的一动点，F为BC边上的一动点，D点坐标为
，求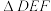周长的最小值；(3)如图2，N为射线CB上的一点，M是抛物线上的一点，M、N均在第一象限内，B、N位于直线AM的同侧，若M到x轴的距离为d，
面积为
，当为等腰三角形时，求点N的坐标．