全一卷
1.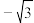 的相反数是( )
的相反数是( )
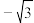 的相反数是( )
的相反数是( )A. | B.- | C. | D.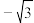 |
2.某几何体的三视图如图所示,则此几何体是( )
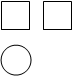

| A.圆锥 | B.圆柱 | C.长方体 | D.四棱柱 |
3.中国人最先使用负数,魏晋时期的数学家刘徽在其著作《九章算术注》中,用不同颜色的算筹(小棍形状的记数工具)分别表示正数和负数(红色为正,黑色为负).如图1表示的是(+2)+(-2),根据这种表示法,可推算出图2所表示的算式是( )


A. | B. |
C. | D. |
4.下列图形中,既是轴对称图形又是中心对称图形的是( )
| A.三角形 | B.等边三角形 |
| C.平行四边形 | D.菱形 |
5.下列命题是真命题的是
| A.同位角相等 | B. 是分式 是分式 |
| C.数据6,3,10的中位数是3 | D.第七次全国人口普查是全面调查 |
6.某市严格落实国家节水政策,2018年用水总量为6.5亿立方米,2020年用水总量为5.265亿立方米.设该市用水总量的年平均降低率是x,那么x满足的方程是( )
A. | B. |
C. | D. |
7.如图, 的内切圆
的内切圆 与
与 分别相切于点D,E,F,连接
分别相切于点D,E,F,连接 ,
, ,
, ,
, ,
, ,则阴影部分的面积为( )
,则阴影部分的面积为( )

 的内切圆
的内切圆 与
与 分别相切于点D,E,F,连接
分别相切于点D,E,F,连接 ,
, ,
, ,
, ,
, ,则阴影部分的面积为( )
,则阴影部分的面积为( )
A. | B. | C. | D. |
8.如图1,动点P从矩形ABCD的顶点A出发,在边AB,BC上沿A→B→C的方向,以1cm/s的速度匀速运动到点C, 的面积S(cm2)随运动时间t(s)变化的函数图象如图2所示,则AB的长是( )
的面积S(cm2)随运动时间t(s)变化的函数图象如图2所示,则AB的长是( )

 的面积S(cm2)随运动时间t(s)变化的函数图象如图2所示,则AB的长是( )
的面积S(cm2)随运动时间t(s)变化的函数图象如图2所示,则AB的长是( )
A. | B. | C. | D. |
9.9的算术平方根是_____ .
10.解决全人类温饱问题是“世界杂交水稻之父”袁隆平先生的毕生追求.2020年中国粮食总产量达到657 000 000吨,已成为世界粮食第一大国.将657 000 000用科学记数法表示为________ .
11.十二边形的内角和是__________
12.计算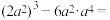
_______ .
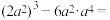
13.从 ,-1,1,2,-5中任取一个数作为a,则抛物线
,-1,1,2,-5中任取一个数作为a,则抛物线 的开口向上的概率是
的开口向上的概率是______ .
 ,-1,1,2,-5中任取一个数作为a,则抛物线
,-1,1,2,-5中任取一个数作为a,则抛物线 的开口向上的概率是
的开口向上的概率是14.如图, 是
是 的直径,弦
的直径,弦 于点E,
于点E, ,
,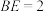 ,则
,则 的半径
的半径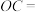
_______ .

 是
是 的直径,弦
的直径,弦 于点E,
于点E, ,
,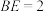 ,则
,则 的半径
的半径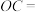

15.如图,在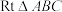 中,
中, ,D,E分别是
,D,E分别是 ,
, 的中点,连接
的中点,连接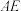 ,
, ,若
,若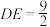 ,
,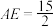 ,则点A到BC的距离是
,则点A到BC的距离是________ .

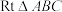 中,
中, ,D,E分别是
,D,E分别是 ,
, 的中点,连接
的中点,连接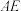 ,
, ,若
,若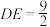 ,
,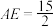 ,则点A到BC的距离是
,则点A到BC的距离是
16.在平面直角坐标系 中,点A的坐标是
中,点A的坐标是 ,若
,若 轴,且
轴,且 ,则点B的坐标是
,则点B的坐标是________ .
 中,点A的坐标是
中,点A的坐标是 ,若
,若 轴,且
轴,且 ,则点B的坐标是
,则点B的坐标是17.如图, 是等边三角形,
是等边三角形, ,N是
,N是 的中点,
的中点, 是
是 边上的中线,M是
边上的中线,M是 上的一个动点,连接
上的一个动点,连接 ,则
,则 的最小值是
的最小值是________ .

 是等边三角形,
是等边三角形, ,N是
,N是 的中点,
的中点, 是
是 边上的中线,M是
边上的中线,M是 上的一个动点,连接
上的一个动点,连接 ,则
,则 的最小值是
的最小值是
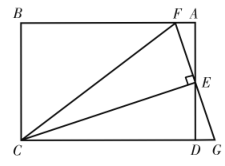
18.如图,在矩形 中,E为
中,E为 的中点,连接
的中点,连接 ,过点E作
,过点E作 的垂线交
的垂线交 于点F,交CD的延长线于点G,连接CF.已知
于点F,交CD的延长线于点G,连接CF.已知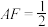 ,
, ,则
,则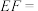
_________ .
 中,E为
中,E为 的中点,连接
的中点,连接 ,过点E作
,过点E作 的垂线交
的垂线交 于点F,交CD的延长线于点G,连接CF.已知
于点F,交CD的延长线于点G,连接CF.已知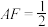 ,
, ,则
,则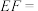

19.计算: 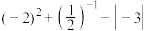 .
.
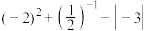 .
.20.解方程: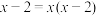 .
.
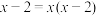 .
.21.计算: .
.
 .
.22.解方程: .
.
 .
.23.如图,四边形 是菱形,对角线
是菱形,对角线 ,
, 相交于点O,
相交于点O, .
.
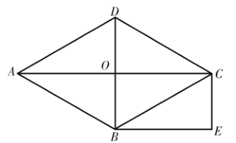
(1)求证:四边形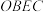 是矩形;
是矩形;
(2)若 ,
,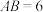 ,求矩形
,求矩形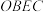 的周长.
的周长.
 是菱形,对角线
是菱形,对角线 ,
, 相交于点O,
相交于点O, .
.
(1)求证:四边形
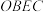 是矩形;
是矩形;(2)若
 ,
,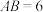 ,求矩形
,求矩形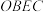 的周长.
的周长.24.如图,正比例函数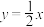 与反比例函数
与反比例函数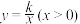 的图象交于点A,
的图象交于点A, 轴于点B,延长AB至点C,连接
轴于点B,延长AB至点C,连接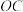 .若
.若 ,
,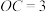 .
.
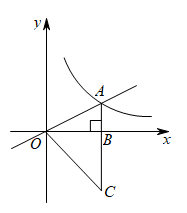
(1)求 的长和反比例函数的解析式;
的长和反比例函数的解析式;
(2)将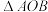 绕点
绕点 旋转90°,请直接写出旋转后点A的对应点A'的坐标.
旋转90°,请直接写出旋转后点A的对应点A'的坐标.
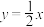 与反比例函数
与反比例函数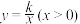 的图象交于点A,
的图象交于点A, 轴于点B,延长AB至点C,连接
轴于点B,延长AB至点C,连接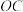 .若
.若 ,
,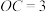 .
.
(1)求
 的长和反比例函数的解析式;
的长和反比例函数的解析式;(2)将
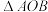 绕点
绕点 旋转90°,请直接写出旋转后点A的对应点A'的坐标.
旋转90°,请直接写出旋转后点A的对应点A'的坐标.25.某校在“庆祝建党100周年”系列活动中举行了主题为“学史明理,学史增信,学史崇德,学史力行”的党史知识竞赛.设竞赛成绩为x分,若规定:当 时为优秀,
时为优秀,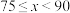 时为良好,
时为良好,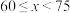 时为一般,现随机抽取30位同学的竞赛成绩如下:
时为一般,现随机抽取30位同学的竞赛成绩如下:
(1)本次抽样调查的样本容量是________,样本数据中成绩为“优秀”的频率是_______;
(2)在本次调查中,A,B,C,D四位同学的竞赛成绩均为100分,其中A,B在九年级,C在八年级,D在七年级,若要从中随机抽取两位同学参加联盟校的党史知识竞赛,请用画树状图或列表的方法求出抽到的两位同学都在九年级的概率,并写出所有等可能结果.
 时为优秀,
时为优秀,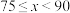 时为良好,
时为良好,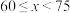 时为一般,现随机抽取30位同学的竞赛成绩如下:
时为一般,现随机抽取30位同学的竞赛成绩如下:| 98 | 88 | 90 | 72 | 100 | 78 | 95 | 92 | 100 | 99 |
| 84 | 92 | 75 | 100 | 85 | 90 | 93 | 93 | 70 | 92 |
| 78 | 89 | 91 | 83 | 93 | 98 | 88 | 85 | 90 | 100 |
(1)本次抽样调查的样本容量是________,样本数据中成绩为“优秀”的频率是_______;
(2)在本次调查中,A,B,C,D四位同学的竞赛成绩均为100分,其中A,B在九年级,C在八年级,D在七年级,若要从中随机抽取两位同学参加联盟校的党史知识竞赛,请用画树状图或列表的方法求出抽到的两位同学都在九年级的概率,并写出所有等可能结果.
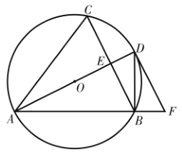
26.如图, 内接于
内接于 ,
, ,
, 是
是 的直径,交
的直径,交 于点E,过点D作
于点E,过点D作 ,交
,交 的延长线于点F,连接
的延长线于点F,连接 .
.
(1)求证: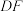 是
是 的切线;
的切线;
(2)已知 ,
,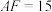 ,求
,求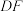 的长.
的长.
 内接于
内接于 ,
, ,
, 是
是 的直径,交
的直径,交 于点E,过点D作
于点E,过点D作 ,交
,交 的延长线于点F,连接
的延长线于点F,连接 .
.
(1)求证:
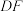 是
是 的切线;
的切线;(2)已知
 ,
,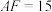 ,求
,求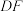 的长.
的长.27.城乡学校集团化办学已成为西宁教育的一张名片.“五四”期间,西宁市某集团校计划组织乡村学校初二年级200名师生到集团总校共同举办“十四岁集体生日”.现需租用A,B两种型号的客车共10辆,两种型号客车的载客量(不包括司机)和租金信息如下表:
若设租用A型客车x辆,租车总费用为y元.
(1)请写出y与x的函数关系式(不要求写自变量取值范围);
(2)据资金预算,本次租车总费用不超过11800元,则A型客车至少需租几辆?
(3)在(2)的条件下,要保证全体师生都有座位,问有哪几种租车方案?请选出最省钱的租车方案.
| 型号 | 载客量(人/辆) | 租金单价(元/辆)A |
| A | 16 | 900 |
| B | 22 | 1200 |
(1)请写出y与x的函数关系式(不要求写自变量取值范围);
(2)据资金预算,本次租车总费用不超过11800元,则A型客车至少需租几辆?
(3)在(2)的条件下,要保证全体师生都有座位,问有哪几种租车方案?请选出最省钱的租车方案.
28.如图,在平面直角坐标系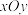 中,一次函数
中,一次函数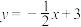 的图象与x轴交于点A,与y轴交于点B,点C的坐标为
的图象与x轴交于点A,与y轴交于点B,点C的坐标为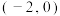 ,抛物线经过A,B,C三点.
,抛物线经过A,B,C三点.
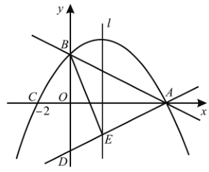
(1)求抛物线的解析式;
(2)直线AD与y轴负半轴交于点D,且 ,求证:
,求证: ;
;
(3)在(2)的条件下,若直线 与抛物线的对称轴l交于点E,连接
与抛物线的对称轴l交于点E,连接 ,在第一象限内的抛物线上是否存在一点P,使四边形
,在第一象限内的抛物线上是否存在一点P,使四边形 的面积最大?若存在,请求出点P的坐标及四边形
的面积最大?若存在,请求出点P的坐标及四边形 面积的最大值;若不存在,请说明理由.
面积的最大值;若不存在,请说明理由.
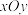 中,一次函数
中,一次函数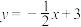 的图象与x轴交于点A,与y轴交于点B,点C的坐标为
的图象与x轴交于点A,与y轴交于点B,点C的坐标为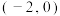 ,抛物线经过A,B,C三点.
,抛物线经过A,B,C三点.
(1)求抛物线的解析式;
(2)直线AD与y轴负半轴交于点D,且
 ,求证:
,求证: ;
;(3)在(2)的条件下,若直线
 与抛物线的对称轴l交于点E,连接
与抛物线的对称轴l交于点E,连接 ,在第一象限内的抛物线上是否存在一点P,使四边形
,在第一象限内的抛物线上是否存在一点P,使四边形 的面积最大?若存在,请求出点P的坐标及四边形
的面积最大?若存在,请求出点P的坐标及四边形 面积的最大值;若不存在,请说明理由.
面积的最大值;若不存在,请说明理由. 搜索
搜索
 难度系数:0.85
难度系数:0.85  答案解析
答案解析
 有奖纠错
有奖纠错
