全一卷
1.6的相反数是( )
A. | B. | C. | D.6 |
2.2020年7月23日,中国首次火星探测任务“天问一号”探测器在海南文昌航天发射场由长征五号遥四运载火箭发射升空,每天基本飞行200万千米,并于2021年5月15日成功着陆预选区,火星上首次留下了中国的足迹.将200万用科学记数法表示为( )
A. | B. | C. | D. |
3.下列计算中,正确的是( )
A. | B. |
C. | D. |
4.如图,将直角三角板放置在矩形纸片上,若 ,则
,则 的度数为( )
的度数为( )

 ,则
,则 的度数为( )
的度数为( )
| A.42° | B.48° | C.52° | D.60° |
5.正八边形中,每个内角与每个外角的度数之比为( )
| A.1:3 | B.1:2 | C.2:1 | D.3:1 |
6.化简 的结果是( )
的结果是( )
 的结果是( )
的结果是( )A. | B. | C. | D. |
7.全民反诈,刻不容缓!陈科同学参加学校举行的“防诈骗”主题演讲比赛,五位评委给出的分数分别为90,80,86,90,94,则这组数据的中位数和众数分别是( )
| A.80,90 | B.90,90 | C.86,90 | D.90,94 |
8.我国某型号运载火箭的整流罩的三视图如图所示,根据图中数据(单位:米)计算该整流罩的侧面积(单位:平方米)是( )


A. | B. | C. | D. |
9.已知一元二次方程 的两根为
的两根为 ,
, ,则
,则 的值为( )
的值为( )
 的两根为
的两根为 ,
, ,则
,则 的值为( )
的值为( )A. | B. | C.2 | D.5 |
10.如图,在以 为直径的
为直径的 中,点
中,点 为圆上的一点,
为圆上的一点, ,弦
,弦 于点
于点 ,弦
,弦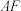 交
交 于点
于点 ,交
,交 于点
于点 .若点
.若点 是
是 的中点,则
的中点,则 的度数为( )
的度数为( )

 为直径的
为直径的 中,点
中,点 为圆上的一点,
为圆上的一点, ,弦
,弦 于点
于点 ,弦
,弦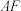 交
交 于点
于点 ,交
,交 于点
于点 .若点
.若点 是
是 的中点,则
的中点,则 的度数为( )
的度数为( )
| A.18° | B.21° | C.22.5° | D.30° |
11.在平面直角坐标系中,抛物线 与
与 轴交于点
轴交于点 ,则该抛物线关于点
,则该抛物线关于点 成中心对称的抛物线的表达式为( )
成中心对称的抛物线的表达式为( )
 与
与 轴交于点
轴交于点 ,则该抛物线关于点
,则该抛物线关于点 成中心对称的抛物线的表达式为( )
成中心对称的抛物线的表达式为( )A. | B. |
C. | D. |
12.如图,在矩形 中,对角线
中,对角线 ,
, 相交于点
相交于点 ,
, ,
, ,点
,点 在线段
在线段 上从点
上从点 至点
至点 运动,连接
运动,连接 ,以
,以 为边作等边三角形
为边作等边三角形 ,点
,点 和点
和点 分别位于
分别位于 两侧,下列结论:①
两侧,下列结论:① ;②
;② ;③
;③ ;④点
;④点 运动的路程是
运动的路程是 ,其中正确结论的序号为( )
,其中正确结论的序号为( )

 中,对角线
中,对角线 ,
, 相交于点
相交于点 ,
, ,
, ,点
,点 在线段
在线段 上从点
上从点 至点
至点 运动,连接
运动,连接 ,以
,以 为边作等边三角形
为边作等边三角形 ,点
,点 和点
和点 分别位于
分别位于 两侧,下列结论:①
两侧,下列结论:① ;②
;② ;③
;③ ;④点
;④点 运动的路程是
运动的路程是 ,其中正确结论的序号为( )
,其中正确结论的序号为( )
| A.①④ | B.①②③ | C.②③④ | D.①②③④ |
13.分解因式:
______ .

14.一次函数 的值随
的值随 值的增大而减少,则常数
值的增大而减少,则常数 的取值范围是
的取值范围是______ .
 的值随
的值随 值的增大而减少,则常数
值的增大而减少,则常数 的取值范围是
的取值范围是15.如图, 中,
中, ,
, ,
, 平分
平分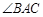 交
交 于点
于点 ,分别以点
,分别以点 和点
和点 为圆心,大于
为圆心,大于 的长为半径作弧,两弧相交于点
的长为半径作弧,两弧相交于点 和点
和点 ,作直线
,作直线 ,交
,交 于点
于点 ,则
,则 的长为
的长为______ .

 中,
中, ,
, ,
, 平分
平分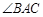 交
交 于点
于点 ,分别以点
,分别以点 和点
和点 为圆心,大于
为圆心,大于 的长为半径作弧,两弧相交于点
的长为半径作弧,两弧相交于点 和点
和点 ,作直线
,作直线 ,交
,交 于点
于点 ,则
,则 的长为
的长为
16.若关于 的不等式
的不等式 只有3个正整数解,则
只有3个正整数解,则 的取值范围是
的取值范围是______ .
 的不等式
的不等式 只有3个正整数解,则
只有3个正整数解,则 的取值范围是
的取值范围是17.观察下列等式: ;
;
 ;
;
 ;
;
……
根据以上规律,计算
______ .
 ;
; ;
; ;
;……
根据以上规律,计算

18.如图,在菱形 中,
中, ,对角线
,对角线 、
、 相交于点
相交于点 ,点
,点 在线段
在线段 上,且
上,且 ,点
,点 为线段
为线段 上的一个动点,则
上的一个动点,则 的最小值是
的最小值是______ .

 中,
中, ,对角线
,对角线 、
、 相交于点
相交于点 ,点
,点 在线段
在线段 上,且
上,且 ,点
,点 为线段
为线段 上的一个动点,则
上的一个动点,则 的最小值是
的最小值是
19.计算: .
.
 .
.20.解方程组

21.吸食毒品极易上瘾,不但对人的健康危害极大,而且严重影响家庭和社会的稳定.为了解同学们对禁毒知识的掌握情况,从我市某校1000名学生中随机抽取部分学生进行问卷调查,调查评价结果分为:“了解较少”,“基本了解”,“了解较多”,“非常了解”四类,并根据调查结果绘制出如图所示的两幅不完整的统计图.


请根据统计图回答下列问题:
(1)本次抽取调查的学生共有 人,其中“了解较多”的占 %;
(2)请补全条形统计图:
(3)估计此校“非常了解”和“了解较多”的学生共有 人;
(4)“了解较少”的四名学生中,有3名学生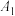 ,
, ,
, 是初一学生,1名学生
是初一学生,1名学生 为初二学生,为了提高学生对禁毒知识的认识,对这4人进行了培训,然后从中随机抽取2人对禁毒知识的掌握情况进行检测.请用画树状图或列表的方法,求恰好抽到初一、初二学生各1名的概率.
为初二学生,为了提高学生对禁毒知识的认识,对这4人进行了培训,然后从中随机抽取2人对禁毒知识的掌握情况进行检测.请用画树状图或列表的方法,求恰好抽到初一、初二学生各1名的概率.


请根据统计图回答下列问题:
(1)本次抽取调查的学生共有 人,其中“了解较多”的占 %;
(2)请补全条形统计图:
(3)估计此校“非常了解”和“了解较多”的学生共有 人;
(4)“了解较少”的四名学生中,有3名学生
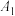 ,
, ,
, 是初一学生,1名学生
是初一学生,1名学生 为初二学生,为了提高学生对禁毒知识的认识,对这4人进行了培训,然后从中随机抽取2人对禁毒知识的掌握情况进行检测.请用画树状图或列表的方法,求恰好抽到初一、初二学生各1名的概率.
为初二学生,为了提高学生对禁毒知识的认识,对这4人进行了培训,然后从中随机抽取2人对禁毒知识的掌握情况进行检测.请用画树状图或列表的方法,求恰好抽到初一、初二学生各1名的概率.22.“眉山水街”走红网络,成为全国各地不少游客新的打卡地!游客小何用无人机对该地一标志建筑物进行拍摄和观测,如图,无人机从 处测得该建筑物顶端
处测得该建筑物顶端 的俯角为24°,继续向该建筑物方向水平飞行20米到达
的俯角为24°,继续向该建筑物方向水平飞行20米到达 处,测得顶端
处,测得顶端 的俯角为45°,已知无人机的飞行高度为60米,则这栋建筑物的高度是多少米?(精确到0.1米,参考数据:
的俯角为45°,已知无人机的飞行高度为60米,则这栋建筑物的高度是多少米?(精确到0.1米,参考数据: ,
, ,
, )
)

 处测得该建筑物顶端
处测得该建筑物顶端 的俯角为24°,继续向该建筑物方向水平飞行20米到达
的俯角为24°,继续向该建筑物方向水平飞行20米到达 处,测得顶端
处,测得顶端 的俯角为45°,已知无人机的飞行高度为60米,则这栋建筑物的高度是多少米?(精确到0.1米,参考数据:
的俯角为45°,已知无人机的飞行高度为60米,则这栋建筑物的高度是多少米?(精确到0.1米,参考数据: ,
, ,
, )
)
23.为进一步落实“德、智、体、美、劳”五育并举工作,某中学以体育为突破口,准备从体育用品商场一次性购买若干个足球和篮球,用于学校球类比赛活动.每个足球的价格都相同,每个篮球的价格也相同.已知篮球的单价比足球单价的2倍少30元,用1200元购买足球的数量是用900元购买篮球数量的2倍.
(1)足球和篮球的单价各是多少元?
(2)根据学校实际情况,需一次性购买足球和篮球共200个,但要求足球和篮球的总费用不超过15500元,学校最多可以购买多少个篮球?
(1)足球和篮球的单价各是多少元?
(2)根据学校实际情况,需一次性购买足球和篮球共200个,但要求足球和篮球的总费用不超过15500元,学校最多可以购买多少个篮球?
24.如图,直线 与
与 轴交于点
轴交于点 ,与
,与 轴交于点
轴交于点 .直线
.直线 ,且与
,且与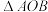 的外接圆
的外接圆 相切,与双曲线
相切,与双曲线 在第二象限内的图象交于
在第二象限内的图象交于 、
、 两点.
两点.
(1)求点 ,
, 的坐标和
的坐标和 的半径;
的半径;
(2)求直线 所对应的函数表达式;
所对应的函数表达式;
(3)求 的面积.
的面积.

 与
与 轴交于点
轴交于点 ,与
,与 轴交于点
轴交于点 .直线
.直线 ,且与
,且与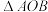 的外接圆
的外接圆 相切,与双曲线
相切,与双曲线 在第二象限内的图象交于
在第二象限内的图象交于 、
、 两点.
两点.(1)求点
 ,
, 的坐标和
的坐标和 的半径;
的半径;(2)求直线
 所对应的函数表达式;
所对应的函数表达式;(3)求
 的面积.
的面积.
25.如图,在等腰直角三角形 中,
中, ,
, ,边长为2的正方形
,边长为2的正方形 的对角线交点与点
的对角线交点与点 重合,连接
重合,连接 ,
,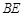 .
.
(1)求证: ;
;
(2)当点 在
在 内部,且
内部,且 时,设
时,设 与
与 相交于点
相交于点 ,求
,求 的长;
的长;
(3)将正方形 绕点
绕点 旋转一周,当点
旋转一周,当点 、
、 、
、 三点在同一直线上时,请直接写出
三点在同一直线上时,请直接写出 的长.
的长.

 中,
中, ,
, ,边长为2的正方形
,边长为2的正方形 的对角线交点与点
的对角线交点与点 重合,连接
重合,连接 ,
,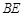 .
.(1)求证:
 ;
;(2)当点
 在
在 内部,且
内部,且 时,设
时,设 与
与 相交于点
相交于点 ,求
,求 的长;
的长;(3)将正方形
 绕点
绕点 旋转一周,当点
旋转一周,当点 、
、 、
、 三点在同一直线上时,请直接写出
三点在同一直线上时,请直接写出 的长.
的长.
26.如图,在平面直角坐标系中,已知抛物线 经过点
经过点 和点
和点 .
.
(1)求这条抛物线所对应的函数表达式;
(2)点 为该抛物线上一点(不与点
为该抛物线上一点(不与点 重合),直线
重合),直线 将
将 的面积分成2:1两部分,求点
的面积分成2:1两部分,求点 的坐标;
的坐标;
(3)点 从点
从点 出发,以每秒1个单位的速度沿
出发,以每秒1个单位的速度沿 轴移动,运动时间为
轴移动,运动时间为 秒,当
秒,当 时,求
时,求 的值.
的值.

 经过点
经过点 和点
和点 .
.(1)求这条抛物线所对应的函数表达式;
(2)点
 为该抛物线上一点(不与点
为该抛物线上一点(不与点 重合),直线
重合),直线 将
将 的面积分成2:1两部分,求点
的面积分成2:1两部分,求点 的坐标;
的坐标;(3)点
 从点
从点 出发,以每秒1个单位的速度沿
出发,以每秒1个单位的速度沿 轴移动,运动时间为
轴移动,运动时间为 秒,当
秒,当 时,求
时,求 的值.
的值.
 搜索
搜索
 难度系数:0.94
难度系数:0.94  答案解析
答案解析
 有奖纠错
有奖纠错
