全一卷
1.2021的倒数是( )
| A.2021 | B.-2021 | C. | D. |
2.下列式子正确的是( )
A. | B. | C. | D. |
3.2021年5月19日,第三届阿里数学竞赛预选赛顺利结束,本届大赛在全球范围内吸引了约5万名数学爱好者参加.阿里数学竞赛旨在全球范围内引领开启关注数学、理解数学、欣赏数学、助力数学的科学风尚.5万用科学记数法表示为( )
A. | B. | C. | D. |
4.一组数据 的中位数和众数是( )
的中位数和众数是( )
 的中位数和众数是( )
的中位数和众数是( )A. | B. | C. | D. |
5.如图,点 在矩形
在矩形 的对角线
的对角线 所在的直线上,
所在的直线上, ,则四边形
,则四边形 是( )
是( )

 在矩形
在矩形 的对角线
的对角线 所在的直线上,
所在的直线上, ,则四边形
,则四边形 是( )
是( )
| A.平行四边形 | B.矩形 | C.菱形 | D.正方形 |
6.如图, ,点
,点 在
在 边上,已知
边上,已知 ,则
,则 的度数为( )
的度数为( )

 ,点
,点 在
在 边上,已知
边上,已知 ,则
,则 的度数为( )
的度数为( )
A. | B. | C. | D. |
7.从背面朝上的分别画有等腰三角形、平行四边形、矩形、圆的四张形状、大小相同的卡片中,随机抽取一张,则所抽得的图形既是中心对称图形又是轴对称图形的概率为( )
A.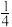 | B. | C.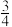 | D.1 |
8. 是某三角形三边的长,则
是某三角形三边的长,则 等于( )
等于( )
 是某三角形三边的长,则
是某三角形三边的长,则 等于( )
等于( )A. | B. | C.10 | D.4 |
9.如图,直线 和
和 与x轴分别相交于点
与x轴分别相交于点 ,点
,点 ,则
,则 解集为( )
解集为( )

 和
和 与x轴分别相交于点
与x轴分别相交于点 ,点
,点 ,则
,则 解集为( )
解集为( )
A. | B. | C. | D. 或 或 |
10.如图,直角坐标系中,以5为半径的动圆的圆心A沿x轴移动,当⊙ 与直线
与直线 只有一个公共点时,点A的坐标为( )
只有一个公共点时,点A的坐标为( )
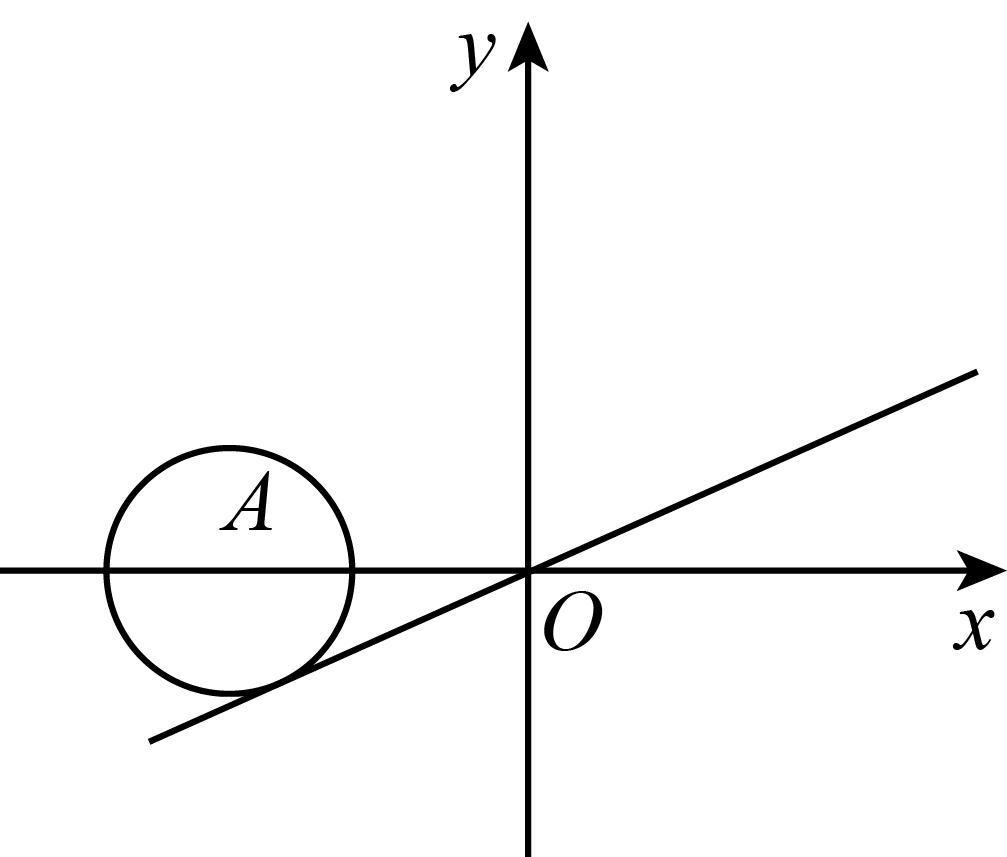
 与直线
与直线 只有一个公共点时,点A的坐标为( )
只有一个公共点时,点A的坐标为( )
A. | B. | C. | D. |
11.根据反比例函数的性质、联系化学学科中的溶质质量分数的求法以及生活体验等,判定下列有关函数 (a为常数且
(a为常数且 )的性质表述中,正确的是( )
)的性质表述中,正确的是( )
①y随x的增大而增大;②y随x的增大而减小;③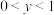 ;④
;④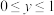
 (a为常数且
(a为常数且 )的性质表述中,正确的是( )
)的性质表述中,正确的是( )①y随x的增大而增大;②y随x的增大而减小;③
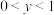 ;④
;④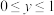
| A.①③ | B.①④ | C.②③ | D.②④ |
12.用数形结合等思想方法确定二次函数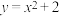 的图象与反比例函数
的图象与反比例函数 的图象的交点的横坐标
的图象的交点的横坐标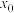 所在的范围是( )
所在的范围是( )
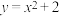 的图象与反比例函数
的图象与反比例函数 的图象的交点的横坐标
的图象的交点的横坐标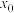 所在的范围是( )
所在的范围是( )A. | B. | C. | D. |
13.函数 中,自变量
中,自变量 的取值范围是
的取值范围是__________ .
 中,自变量
中,自变量 的取值范围是
的取值范围是14.如图所示的扇形中,已知 ,则
,则
________ .

 ,则
,则

15.如图, 中,
中, 是
是 上任意一点,
上任意一点, 于点
于点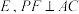 于点F,若
于点F,若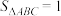 ,则
,则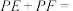
________ .

 中,
中, 是
是 上任意一点,
上任意一点, 于点
于点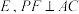 于点F,若
于点F,若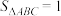 ,则
,则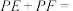

16.已知 ,则
,则
________ .
 ,则
,则
17.高速公路上有一种标线叫纵向减速标线,外号叫鱼骨线,作用是为了提醒驾驶员在开车时减速慢行.如图,用平行四边形 表示一个“鱼骨”,
表示一个“鱼骨”, 平行于车辆前行方向,
平行于车辆前行方向, ,过B作
,过B作 的垂线,垂足为
的垂线,垂足为 (A点的视觉错觉点),若
(A点的视觉错觉点),若 ,则
,则
________  .
.


 表示一个“鱼骨”,
表示一个“鱼骨”, 平行于车辆前行方向,
平行于车辆前行方向, ,过B作
,过B作 的垂线,垂足为
的垂线,垂足为 (A点的视觉错觉点),若
(A点的视觉错觉点),若 ,则
,则
 .
.

18.弧度是表示角度大小的一种单位,圆心角所对的弧长和半径相等时,这个角就是1弧度角,记作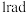 .已知
.已知 ,则
,则 与
与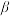 的大小关系是
的大小关系是
________ 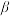 .
.

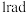 .已知
.已知 ,则
,则 与
与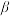 的大小关系是
的大小关系是
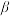 .
.
19.计算: .
.
 .
.20.先化简,再求值: ,其中x是
,其中x是 中的一个合适的数.
中的一个合适的数.
 ,其中x是
,其中x是 中的一个合适的数.
中的一个合适的数.21.“读书,点亮未来”,广泛的课外阅读是同学们搜集和汲取知识的一条重要途径.学校图书馆计划购进一批学生喜欢的图书,为了了解学生们对“A文史类、B科普类、C生活类、D其它”的喜欢程度,随机抽取了部分学生进行问卷调查(每个学生只选其中一类),将所得数据进行分类统计绘制了如下不完整的统计图表,请根据图中的信息,解答下列问题:
统计表:
(1)本次调查的学生共_______人;
(2) _______,
_______, _______;
_______;
(3)补全条形统计图.

统计表:
| 频数 | 频率 | |
| A历史类 | 50 | m |
| B科普类 | 90 | 0.45 |
| C生活类 | n | 0.20 |
| D其它 | 20 | 0.10 |
| 合计 |
(2)
 _______,
_______, _______;
_______;(3)补全条形统计图.

22.我国航天事业捷报频传,天舟二号于2021年5月29日成功发射,震撼人心.当天舟二号从地面到达点A处时,在P处测得A点的仰角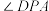 为
为 且A与P两点的距离为6千米,它沿铅垂线上升7.5秒后到达B处,此时在P处测得B点的仰角
且A与P两点的距离为6千米,它沿铅垂线上升7.5秒后到达B处,此时在P处测得B点的仰角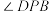 为
为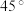 ,求天舟二号从A处到B处的平均速度.(结果精确到
,求天舟二号从A处到B处的平均速度.(结果精确到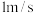 ,取
,取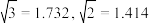 )
)

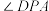 为
为 且A与P两点的距离为6千米,它沿铅垂线上升7.5秒后到达B处,此时在P处测得B点的仰角
且A与P两点的距离为6千米,它沿铅垂线上升7.5秒后到达B处,此时在P处测得B点的仰角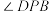 为
为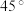 ,求天舟二号从A处到B处的平均速度.(结果精确到
,求天舟二号从A处到B处的平均速度.(结果精确到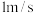 ,取
,取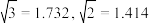 )
)
23.为了庆祝中国共产党建党一百周年,某校举行“礼赞百年,奋斗有我”演讲比赛,准备购买甲、乙两种纪念品奖励在活动中表现优秀的学生.已知购买1个甲种纪念品和2个乙种纪念品共需20元,购买2个甲种纪念品和5个乙种纪念品共需45元.
(1)求购买一个甲种纪念品和一个乙种纪念品各需多少元;
(2)若要购买这两种纪念品共100个,投入资金不少于766元又不多于800元,问有多少种购买方案?并求出所花资金的最小值.
(1)求购买一个甲种纪念品和一个乙种纪念品各需多少元;
(2)若要购买这两种纪念品共100个,投入资金不少于766元又不多于800元,问有多少种购买方案?并求出所花资金的最小值.
24.如图,点A在以 为直径的⊙
为直径的⊙ 上,
上, 的角平分线与
的角平分线与 相交于点E,与⊙
相交于点E,与⊙ 相交于点D,延长
相交于点D,延长 至M,连结
至M,连结 ,使得
,使得 ,过点A作
,过点A作 的平行线与
的平行线与 的延长线交于点N.
的延长线交于点N.
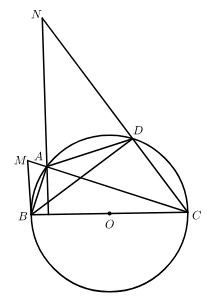
(1)求证: 与⊙
与⊙ 相切;
相切;
(2)试给出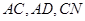 之间的数量关系,并予以证明.
之间的数量关系,并予以证明.
 为直径的⊙
为直径的⊙ 上,
上, 的角平分线与
的角平分线与 相交于点E,与⊙
相交于点E,与⊙ 相交于点D,延长
相交于点D,延长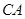 至M,连结
至M,连结 ,使得
,使得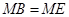 ,过点A作
,过点A作 的平行线与
的平行线与 的延长线交于点N.
的延长线交于点N.
(1)求证:
 与⊙
与⊙ 相切;
相切;(2)试给出
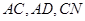 之间的数量关系,并予以证明.
之间的数量关系,并予以证明.25.如图①, 是等腰
是等腰 的斜边
的斜边 上的两动点,
上的两动点, 且
且 .
.


(1)求证: ;
;
(2)求证: ;
;
(3)如图②,作 ,垂足为H,设
,垂足为H,设 ,不妨设
,不妨设 ,请利用(2)的结论证明:当
,请利用(2)的结论证明:当 时,
时, 成立.
成立.
 是等腰
是等腰 的斜边
的斜边 上的两动点,
上的两动点, 且
且 .
.

(1)求证:
 ;
;(2)求证:
 ;
;(3)如图②,作
 ,垂足为H,设
,垂足为H,设 ,不妨设
,不妨设 ,请利用(2)的结论证明:当
,请利用(2)的结论证明:当 时,
时, 成立.
成立.26.如图,在直角坐标系中,二次函数 的图象与x轴相交于点
的图象与x轴相交于点 和点
和点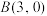 ,与y轴交于点C.
,与y轴交于点C.

(1)求 的值;
的值;
(2)点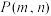 为抛物线上的动点,过P作x轴的垂线交直线
为抛物线上的动点,过P作x轴的垂线交直线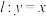 于点Q.
于点Q.
①当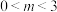 时,求当P点到直线
时,求当P点到直线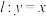 的距离最大时m的值;
的距离最大时m的值;
②是否存在m,使得以点 为顶点的四边形是菱形,若不存在,请说明理由;若存在,请求出m的值.
为顶点的四边形是菱形,若不存在,请说明理由;若存在,请求出m的值.
 的图象与x轴相交于点
的图象与x轴相交于点 和点
和点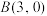 ,与y轴交于点C.
,与y轴交于点C.
(1)求
 的值;
的值;(2)点
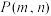 为抛物线上的动点,过P作x轴的垂线交直线
为抛物线上的动点,过P作x轴的垂线交直线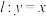 于点Q.
于点Q.①当
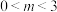 时,求当P点到直线
时,求当P点到直线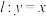 的距离最大时m的值;
的距离最大时m的值;②是否存在m,使得以点
 为顶点的四边形是菱形,若不存在,请说明理由;若存在,请求出m的值.
为顶点的四边形是菱形,若不存在,请说明理由;若存在,请求出m的值. 搜索
搜索
 难度系数:0.94
难度系数:0.94  答案解析
答案解析
 有奖纠错
有奖纠错
