全一卷
1.6的相反数为



| A.-6 | B.6 | C. | D. |
2.如图,直线 //
// ,
, ,则
,则 等于( )
等于( )

 //
// ,
, ,则
,则 等于( )
等于( )
| A.24° | B.42° | C.48° | D.132° |
3.某校九年级各班少数民族学生人数分别为:6,8,10,9,10,8,10,这组数据的众数是( )
| A.6 | B.8 | C.9 | D.10 |
4.下列图案不是轴对称图形的是( )
A. | B. | C. | D. |
5.在反比例函数 中,当
中,当 时,y的值为( )
时,y的值为( )
 中,当
中,当 时,y的值为( )
时,y的值为( )| A.2 | B.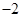 | C. | D. |
6.如图,该几何体的主视图是( )


A. | B. | C. | D. |
7.多项式 因式分解为( )
因式分解为( )
 因式分解为( )
因式分解为( )A. | B. |
C. | D. |
8.如图,在 中,点D,E分别在AB,AC上,且
中,点D,E分别在AB,AC上,且 ,若
,若 //
// ,则
,则 等于( )
等于( )

 中,点D,E分别在AB,AC上,且
中,点D,E分别在AB,AC上,且 ,若
,若 //
// ,则
,则 等于( )
等于( )
| A.1∶2 | B.1∶3 | C.1∶4 | D.1∶9 |
9.已知一次函数 的图象过二、三、四象限,则下列结论正确的是( )
的图象过二、三、四象限,则下列结论正确的是( )
 的图象过二、三、四象限,则下列结论正确的是( )
的图象过二、三、四象限,则下列结论正确的是( )A. , , | B. , , |
C. , , | D. , , |
10.如图,将两个完全相同的Rt△ACB和Rt△A'C′B′拼在一起,其中点A′与点B重合,点C'在边AB上,连接B′C,若∠ABC=∠A′B′C′=30°,AC=A′C′=2,则B′C的长为( )


A.2 | B.4 | C.2 | D.4 |
11.如图,四边形ABCD内接于 ,
, ,
, ,则
,则 的长度是( )
的长度是( )

 ,
, ,
, ,则
,则 的长度是( )
的长度是( )
A. | B. | C. | D. |
12.我国宋代数学家杨辉发现了 (
( ,1,2,3,…)展开式系数的规律:
,1,2,3,…)展开式系数的规律:

以上系数三角表称为“杨辉三角”,根据上述规律, 展开式的系数和是( )
展开式的系数和是( )
 (
( ,1,2,3,…)展开式系数的规律:
,1,2,3,…)展开式系数的规律:
以上系数三角表称为“杨辉三角”,根据上述规律,
 展开式的系数和是( )
展开式的系数和是( )| A.64 | B.128 | C.256 | D.612 |
13.受新冠肺炎疫情影响,2020年高考于7月7日开考,据了解我区今年参加高考的考生人数约为507000人,数据507000用科学记数法表示为________ .
14.在平面直角坐标系中,点 关于x轴对称的点的坐标是
关于x轴对称的点的坐标是________ .
 关于x轴对称的点的坐标是
关于x轴对称的点的坐标是15.若一组数据1,2,x,5,5,6的平均数是4,则x=__ .
16.函数 中,自变量x的取值范围是
中,自变量x的取值范围是________ .
 中,自变量x的取值范围是
中,自变量x的取值范围是17.某学生在一平地上推铅球,铅球出手时离地面的高度为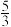 米,出手后铅球在空中运动的高度y(米)与水平距离x(米)之间的函数关系式为
米,出手后铅球在空中运动的高度y(米)与水平距离x(米)之间的函数关系式为 ,当铅球运行至与出手高度相等时,与出手点水平距离为8米,则该学生推铅球的成绩为
,当铅球运行至与出手高度相等时,与出手点水平距离为8米,则该学生推铅球的成绩为________ 米.
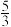 米,出手后铅球在空中运动的高度y(米)与水平距离x(米)之间的函数关系式为
米,出手后铅球在空中运动的高度y(米)与水平距离x(米)之间的函数关系式为 ,当铅球运行至与出手高度相等时,与出手点水平距离为8米,则该学生推铅球的成绩为
,当铅球运行至与出手高度相等时,与出手点水平距离为8米,则该学生推铅球的成绩为18.如图,四边形ABCD是菱形,对角线AC,BD相交于点O, ,
, ,点P是AC上一动点,点E是AB的中点,则
,点P是AC上一动点,点E是AB的中点,则 的最小值为
的最小值为________ .

 ,
, ,点P是AC上一动点,点E是AB的中点,则
,点P是AC上一动点,点E是AB的中点,则 的最小值为
的最小值为
19.计算: .
.
 .
.20.解方程组: .
.
 .
.21.如图,一个可以自由转动的均匀转盘被三等分,分别标有1,2,3三个数字,甲、乙两人玩游戏,规则如下:甲先转动转盘,转盘停止后,指针指向一个数字所在的扇形(如果指针恰好指在分格线上,那么重转一次,直到指针指向某一数字为止),然后乙同样转动转盘,再将两人转得的数字相加,如果两个数字和是奇数则甲胜,否则乙胜.请根据游戏规则完成下列问题:

(1)用画树状图或列表法求甲胜的概率;
(2)这个游戏对两人公平吗?请说明理由.

(1)用画树状图或列表法求甲胜的概率;
(2)这个游戏对两人公平吗?请说明理由.
22.如图,小丽站在电子显示屏正前方5m远的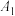 处看“防溺水六不准”,她看显示屏顶端B的仰角为60°,显示屏底端C的仰角为45°,已知小丽的眼睛与地面距离
处看“防溺水六不准”,她看显示屏顶端B的仰角为60°,显示屏底端C的仰角为45°,已知小丽的眼睛与地面距离 ,求电子显示屏高BC的值.(结果保留一位小数,参考数据:
,求电子显示屏高BC的值.(结果保留一位小数,参考数据: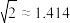 ,
, ).
).

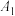 处看“防溺水六不准”,她看显示屏顶端B的仰角为60°,显示屏底端C的仰角为45°,已知小丽的眼睛与地面距离
处看“防溺水六不准”,她看显示屏顶端B的仰角为60°,显示屏底端C的仰角为45°,已知小丽的眼睛与地面距离 ,求电子显示屏高BC的值.(结果保留一位小数,参考数据:
,求电子显示屏高BC的值.(结果保留一位小数,参考数据: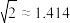 ,
, ).
).
23.如图,已知在△ABC中AB=AC,AD是BC边上的中线,E,G分别是AC,DC的中点,F为DE延长线上的点,∠FCA=∠CEG.
(1)求证:AD∥CF;
(2)求证:四边形ADCF是矩形.

(1)求证:AD∥CF;
(2)求证:四边形ADCF是矩形.

24.今年夏天,多地连降大雨,某地因大雨导致山体塌方,致使车辆通行受阻,某工程队紧急抢修,需要爆破作业.现有A,B两种导火索,A种导火索的燃烧速度是B种导火索燃烧速度的 ,同样燃烧长度为36cm的导火索,A种所需时间比B种多
,同样燃烧长度为36cm的导火索,A种所需时间比B种多 .
.
(1)求A,B两种导火索的燃烧速度分别是多少?
(2)为了安全考虑,工人选燃烧速度慢的导火索进行爆破,一工人点燃导火索后以6m/s的速度跑到距爆破点100m外的安全区,问至少需要该种导火索多长?
 ,同样燃烧长度为36cm的导火索,A种所需时间比B种多
,同样燃烧长度为36cm的导火索,A种所需时间比B种多 .
.(1)求A,B两种导火索的燃烧速度分别是多少?
(2)为了安全考虑,工人选燃烧速度慢的导火索进行爆破,一工人点燃导火索后以6m/s的速度跑到距爆破点100m外的安全区,问至少需要该种导火索多长?
25.如图, 是
是 的直径,
的直径, 是
是 延长线上的一点,点
延长线上的一点,点 在
在 上,
上, 交
交 的延长线于点
的延长线于点 ,
, 平分
平分 .
.

(1)求证: 是
是 的切线;
的切线;
(2)若 ,求
,求 的直径.
的直径.
 是
是 的直径,
的直径, 是
是 延长线上的一点,点
延长线上的一点,点 在
在 上,
上, 交
交 的延长线于点
的延长线于点 ,
, 平分
平分 .
.
(1)求证:
 是
是 的切线;
的切线;(2)若
 ,求
,求 的直径.
的直径.26.如图,抛物线 与
与 轴交于点
轴交于点 ,顶点为
,顶点为 .
.

(1)求该抛物线的解析式;
(2)平行于 轴的直线与抛物线交于
轴的直线与抛物线交于 两点(点
两点(点 在点
在点 的右边),若
的右边),若 ,求
,求 两点的坐标;
两点的坐标;
(3)在(2)的条件下,若点 是线段
是线段 上的动点,经过点
上的动点,经过点 的直线
的直线 与
与 轴交于点
轴交于点 ,连接
,连接 ,求
,求 的面积的最大值和最小值.
的面积的最大值和最小值.
 与
与 轴交于点
轴交于点 ,顶点为
,顶点为 .
.
(1)求该抛物线的解析式;
(2)平行于
 轴的直线与抛物线交于
轴的直线与抛物线交于 两点(点
两点(点 在点
在点 的右边),若
的右边),若 ,求
,求 两点的坐标;
两点的坐标;(3)在(2)的条件下,若点
 是线段
是线段 上的动点,经过点
上的动点,经过点 的直线
的直线 与
与 轴交于点
轴交于点 ,连接
,连接 ,求
,求 的面积的最大值和最小值.
的面积的最大值和最小值. 搜索
搜索
 难度系数:0.94
难度系数:0.94  答案解析
答案解析
 有奖纠错
有奖纠错
