全一卷
1.截至2021年6月8日,31个省(自治区,直辖市)和新疆生产建设兵团累计报告接种新冠病毒疫苗超过800000000次,用科学记数法表示800000000是( )
A. | B. | C. | D. |
2.计算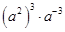 的结果是( )
的结果是( )
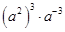 的结果是( )
的结果是( )A.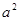 | B. | C. | D. |
3.下列长度的三条线段与长度为5的线段能组成四边形的是( )
| A.1,1,1 | B.1,1,8 | C.1,2,2 | D.2,2,2 |
4.北京与莫斯科的时差为5小时,例如,北京时间13:00,同一时刻的莫斯科时间是8:00,小丽和小红分别在北京和莫斯科,她们相约在各自当地时间9:00~17:00之间选择一个时刻开始通话,这个时刻可以是北京时间( )
| A.10:00 | B.12:00 | C.15:00 | D.18:00 |
5.一般地,如果 (n为正整数,且
(n为正整数,且 ),那么x叫做a的n次方根,下列结论中正确的是( )
),那么x叫做a的n次方根,下列结论中正确的是( )
 (n为正整数,且
(n为正整数,且 ),那么x叫做a的n次方根,下列结论中正确的是( )
),那么x叫做a的n次方根,下列结论中正确的是( )| A.16的4次方根是2 | B.32的5次方根是 |
| C.当n为奇数时,2的n次方根随n的增大而减小 | D.当n为奇数时,2的n次方根随n的增大而增大 |
6.如图,正方形纸板的一条对角线重直于地面,纸板上方的灯(看作一个点)与这条对角线所确定的平面垂直于纸板,在灯光照射下,正方形纸板在地面上形成的影子的形状可以是( )
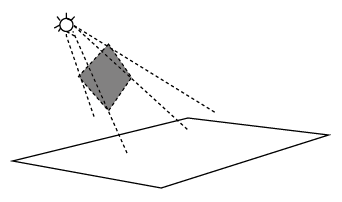

A. | B. |
C. | |
D. |
7.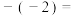
________ ;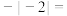
________ .
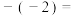
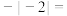
8.若式子 在实数范围内有意义,则x的取值范围是
在实数范围内有意义,则x的取值范围是________ .
 在实数范围内有意义,则x的取值范围是
在实数范围内有意义,则x的取值范围是9.计算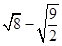 的结果是
的结果是________ .
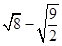 的结果是
的结果是10.设 是关于x的方程
是关于x的方程 的两个根,且
的两个根,且 ,则
,则
_______ .
 是关于x的方程
是关于x的方程 的两个根,且
的两个根,且 ,则
,则
11.如图,在平面直角坐标系中, 的边
的边 的中点C,D的横坐标分别是1,4,则点B的横坐标是
的中点C,D的横坐标分别是1,4,则点B的横坐标是_______ .

 的边
的边 的中点C,D的横坐标分别是1,4,则点B的横坐标是
的中点C,D的横坐标分别是1,4,则点B的横坐标是
12.如图, 是
是 的弦,C是
的弦,C是 的中点,
的中点, 交
交 于点D.若
于点D.若 ,则
,则 的半径为
的半径为________  .
.

 是
是 的弦,C是
的弦,C是 的中点,
的中点, 交
交 于点D.若
于点D.若 ,则
,则 的半径为
的半径为 .
.
13.如图,正比例函数 与函数
与函数 的图像交于A,B两点,
的图像交于A,B两点, 轴,
轴, 轴,则
轴,则
________ .

 与函数
与函数 的图像交于A,B两点,
的图像交于A,B两点, 轴,
轴, 轴,则
轴,则

14.如图, 是五边形
是五边形 的外接圆的切线,则
的外接圆的切线,则
______  .
.

 是五边形
是五边形 的外接圆的切线,则
的外接圆的切线,则
 .
.
15.如图,在四边形 中,
中, .设
.设 ,则
,则
______ (用含 的代数式表示).
的代数式表示).

 中,
中, .设
.设 ,则
,则
 的代数式表示).
的代数式表示).
16.如图,将 绕点A逆时针旋转到
绕点A逆时针旋转到 的位置,使点
的位置,使点 落在
落在 上,
上, 与
与 交于点E,若
交于点E,若 ,则
,则 的长为
的长为________ .

 绕点A逆时针旋转到
绕点A逆时针旋转到 的位置,使点
的位置,使点 落在
落在 上,
上, 与
与 交于点E,若
交于点E,若 ,则
,则 的长为
的长为
17.解不等式 ,并在数轴上表示解集.
,并在数轴上表示解集.
 ,并在数轴上表示解集.
,并在数轴上表示解集.18.解方程 .
.
 .
.19.计算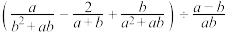 .
.
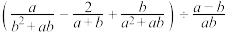 .
.20.如图, 与
与 交于点O,
交于点O,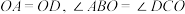 ,E为
,E为 延长线上一点,过点E作
延长线上一点,过点E作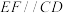 ,交
,交 的延长线于点F.
的延长线于点F.
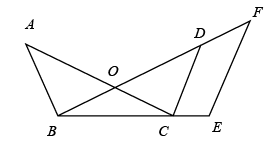
(1)求证 ;
;
(2)若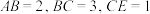 ,求
,求 的长.
的长.
 与
与 交于点O,
交于点O,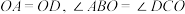 ,E为
,E为 延长线上一点,过点E作
延长线上一点,过点E作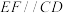 ,交
,交 的延长线于点F.
的延长线于点F.
(1)求证
 ;
;(2)若
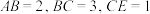 ,求
,求 的长.
的长.21.某市在实施居民用水定额管理前,对居民生活用水情况进行了调查,通过简单随机抽样,获得了100个家庭去年的月均用水量数据,将这组数据按从小到大的顺序排列,其中部分数据如下表:
(1)求这组数据的中位数.已知这组数据的平均数为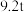 ,你对它与中位数的差异有什么看法?
,你对它与中位数的差异有什么看法?
(2)为了鼓励节约用水,要确定一个用水量的标准,超出这个标准的部分按1.5倍价格收费,若要使75%的家庭水费支出不受影响,你觉得这个标准应该定为多少?
| 序号 | 1 | 2 | … | 25 | 26 | … | 50 | 51 | … | 75 | 76 | … | 99 | 100 |
| 月均用水量/t | 1.3 | 1.3 | … | 4.5 | 4.5 | … | 6.4 | 6.8 | … | 11 | 13 | … | 25.6 | 28 |
(1)求这组数据的中位数.已知这组数据的平均数为
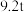 ,你对它与中位数的差异有什么看法?
,你对它与中位数的差异有什么看法?(2)为了鼓励节约用水,要确定一个用水量的标准,超出这个标准的部分按1.5倍价格收费,若要使75%的家庭水费支出不受影响,你觉得这个标准应该定为多少?
22.不透明的袋子中装有2个红球、1个白球,这些球除颜色外无其他差别.
(1)从袋子中随机摸出1个球,放回并摇匀,再随机摸出1个球.求两次摸出的球都是红球的概率.
(2)从袋子中随机摸出1个球,如果是红球,不放回再随机换出1个球;如果是白球,放回并摇匀,再随机摸出1个球.两次摸出的球都是白球的概率是________.
(1)从袋子中随机摸出1个球,放回并摇匀,再随机摸出1个球.求两次摸出的球都是红球的概率.
(2)从袋子中随机摸出1个球,如果是红球,不放回再随机换出1个球;如果是白球,放回并摇匀,再随机摸出1个球.两次摸出的球都是白球的概率是________.
23.如图,为了测量河对岸两点A,B之间的距离,在河岸这边取点C,D.测得 ,
, ,
, ,
, ,
, ,设A,B,C,D在同一平面内,求A,B两点之间的距离.(参考数据:
,设A,B,C,D在同一平面内,求A,B两点之间的距离.(参考数据: .)
.)

 ,
, ,
, ,
, ,
, ,设A,B,C,D在同一平面内,求A,B两点之间的距离.(参考数据:
,设A,B,C,D在同一平面内,求A,B两点之间的距离.(参考数据: .)
.)
24.甲、乙两人沿同一直道从A地去B地,甲比乙早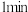 出发,乙的速度是甲的2倍.在整个行程中,甲离A地的距离
出发,乙的速度是甲的2倍.在整个行程中,甲离A地的距离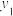 (单位:m)与时间x(单位:
(单位:m)与时间x(单位: )之间的函数关系如图所示.
)之间的函数关系如图所示.
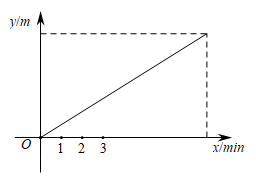
(1)在图中画出乙离A地的距离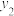 (单位:m)与时间x之间的函数图;
(单位:m)与时间x之间的函数图;
(2)若甲比乙晚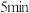 到达B地,求甲整个行程所用的时间.
到达B地,求甲整个行程所用的时间.
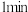 出发,乙的速度是甲的2倍.在整个行程中,甲离A地的距离
出发,乙的速度是甲的2倍.在整个行程中,甲离A地的距离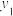 (单位:m)与时间x(单位:
(单位:m)与时间x(单位: )之间的函数关系如图所示.
)之间的函数关系如图所示.
(1)在图中画出乙离A地的距离
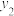 (单位:m)与时间x之间的函数图;
(单位:m)与时间x之间的函数图;(2)若甲比乙晚
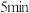 到达B地,求甲整个行程所用的时间.
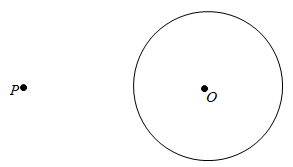
到达B地,求甲整个行程所用的时间.25.如图,已知P是 外一点.用两种不同的方法过点P作
外一点.用两种不同的方法过点P作 的一条切线.要求:
的一条切线.要求:
(1)用直尺和圆规作图;
(2)保留作图的痕迹,写出必要的文字说明.
 外一点.用两种不同的方法过点P作
外一点.用两种不同的方法过点P作 的一条切线.要求:
的一条切线.要求:(1)用直尺和圆规作图;
(2)保留作图的痕迹,写出必要的文字说明.

26.已知二次函数 的图像经过
的图像经过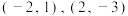 两点.
两点.
(1)求b的值.
(2)当 时,该函数的图像的顶点的纵坐标的最小值是________.
时,该函数的图像的顶点的纵坐标的最小值是________.
(3)设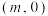 是该函数的图像与x轴的一个公共点,当
是该函数的图像与x轴的一个公共点,当 时,结合函数的图像,直接写出a的取值范围.
时,结合函数的图像,直接写出a的取值范围.
 的图像经过
的图像经过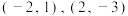 两点.
两点.(1)求b的值.
(2)当
 时,该函数的图像的顶点的纵坐标的最小值是________.
时,该函数的图像的顶点的纵坐标的最小值是________.(3)设
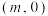 是该函数的图像与x轴的一个公共点,当
是该函数的图像与x轴的一个公共点,当 时,结合函数的图像,直接写出a的取值范围.
时,结合函数的图像,直接写出a的取值范围.27.在几何体表面上,蚂蚁怎样爬行路径最短?
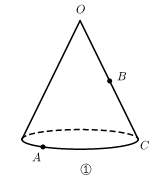
(1)如图①,圆锥的母线长为 ,B为母线
,B为母线 的中点,点A在底面圆周上,
的中点,点A在底面圆周上,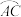 的长为
的长为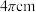 .在图②所示的圆锥的侧面展开图中画出蚂蚁从点A爬行到点B的最短路径,并标出它的长(结果保留根号).
.在图②所示的圆锥的侧面展开图中画出蚂蚁从点A爬行到点B的最短路径,并标出它的长(结果保留根号).
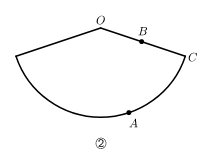
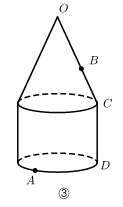
(2)图③中的几何体由底面半径相同的圆锥和圆柱组成.O是圆锥的顶点,点A在圆柱的底面圆周上.设圆锥的母线长为l,圆柱的高为h.
①蚂蚁从点A爬行到点O的最短路径的长为________(用含l,h的代数式表示).
②设 的长为a,点B在母线
的长为a,点B在母线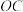 上,
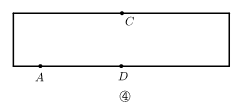
上,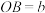 .圆柱的侧面展开图如图④所示,在图中画出蚂蚁从点A爬行到点B的最短路径的示意图,并写出求最短路径的长的思路.
.圆柱的侧面展开图如图④所示,在图中画出蚂蚁从点A爬行到点B的最短路径的示意图,并写出求最短路径的长的思路.
(1)如图①,圆锥的母线长为
 ,B为母线
,B为母线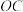 的中点,点A在底面圆周上,
的中点,点A在底面圆周上,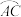 的长为
的长为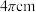 .在图②所示的圆锥的侧面展开图中画出蚂蚁从点A爬行到点B的最短路径,并标出它的长(结果保留根号).
.在图②所示的圆锥的侧面展开图中画出蚂蚁从点A爬行到点B的最短路径,并标出它的长(结果保留根号).

(2)图③中的几何体由底面半径相同的圆锥和圆柱组成.O是圆锥的顶点,点A在圆柱的底面圆周上.设圆锥的母线长为l,圆柱的高为h.
①蚂蚁从点A爬行到点O的最短路径的长为________(用含l,h的代数式表示).
②设
 的长为a,点B在母线
的长为a,点B在母线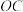 上,
上,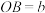 .圆柱的侧面展开图如图④所示,在图中画出蚂蚁从点A爬行到点B的最短路径的示意图,并写出求最短路径的长的思路.
.圆柱的侧面展开图如图④所示,在图中画出蚂蚁从点A爬行到点B的最短路径的示意图,并写出求最短路径的长的思路.

 搜索
搜索
 难度系数:0.94
难度系数:0.94  答案解析
答案解析
 有奖纠错
有奖纠错
