全一卷
1. 的值为( )
的值为( )
 的值为( )
的值为( )A.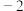 | B.2 | C.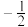 | D. |
2.据报道,我省今年前4个月货物贸易进出口总值为52860 000 000元人民币,比去年同期增长28.2%.其中52860000 000这个数用科学记数法表示为( )
A. | B. | C. | D. |
3.如图是一个几何体的三视图,这个几何体是( )


| A.圆锥 | B.长方体 | C.球 | D.圆柱 |
4.关于x的一元二次方程 有两个不相等的实数根,则m的值可能是( )
有两个不相等的实数根,则m的值可能是( )
 有两个不相等的实数根,则m的值可能是( )
有两个不相等的实数根,则m的值可能是( )| A.8 | B.9 | C.10 | D.11 |
5.如图是净月潭国家森林公园一段索道的示意图.已知A、B两点间的距离为30米, ,则缆车从A点到达B点,上升的高度(BC的长)为( )
,则缆车从A点到达B点,上升的高度(BC的长)为( )


 ,则缆车从A点到达B点,上升的高度(BC的长)为( )
,则缆车从A点到达B点,上升的高度(BC的长)为( )

A. 米 米 | B. 米 米 | C. 米 米 | D. 米 米 |
6.如图,AB是 的直径,BC是
的直径,BC是 的切线,若
的切线,若 ,则
,则 的大小为( )
的大小为( )

 的直径,BC是
的直径,BC是 的切线,若
的切线,若 ,则
,则 的大小为( )
的大小为( )
A.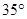 | B.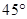 | C. | D. |
7.在 中,
中, ,
, .用无刻度的直尺和圆规在BC边上找一点D,使
.用无刻度的直尺和圆规在BC边上找一点D,使 为等腰三角形.下列作法不正确的是( )
为等腰三角形.下列作法不正确的是( )
 中,
中, ,
, .用无刻度的直尺和圆规在BC边上找一点D,使
.用无刻度的直尺和圆规在BC边上找一点D,使 为等腰三角形.下列作法不正确的是( )
为等腰三角形.下列作法不正确的是( )A. | B. |
C. | D. |
8.如图,在平面直角坐标系中,点A、B在函数 的图象上,x过点A作x轴的垂线,与函数
的图象上,x过点A作x轴的垂线,与函数 的图象交于点C,连结BC交x轴于点D.若点A的横坐标为1,
的图象交于点C,连结BC交x轴于点D.若点A的横坐标为1, ,则点B的横坐标为( )
,则点B的横坐标为( )

 的图象上,x过点A作x轴的垂线,与函数
的图象上,x过点A作x轴的垂线,与函数 的图象交于点C,连结BC交x轴于点D.若点A的横坐标为1,
的图象交于点C,连结BC交x轴于点D.若点A的横坐标为1, ,则点B的横坐标为( )
,则点B的横坐标为( )
A. | B. | C. | D. |
9.分解因式:
_____ .

10.不等式组 的所有整数解是
的所有整数解是__________ .
 的所有整数解是
的所有整数解是11.将一副三角板按如图所示的方式摆放,点D在边AC上, ,则
,则 的大小为
的大小为_______ 度.

 ,则
,则 的大小为
的大小为
12.如图是圆弧形状的铁轨示意图,半径OA的长度为200米,圆心角 ,则这段铁轨的长度
,则这段铁轨的长度_____ 米,(铁轨的宽度忽略不计,结果保留π)

 ,则这段铁轨的长度
,则这段铁轨的长度
13.如图,在平面直角坐标系中,等腰直角三角形AOB的斜边OA在y轴上, ,点B在第一象限.标记点B的位置后,将
,点B在第一象限.标记点B的位置后,将 沿x轴正方向平移至
沿x轴正方向平移至 的位置,使
的位置,使 经过点B,再标记点
经过点B,再标记点 的位置,继续平移至
的位置,继续平移至 的位置,使
的位置,使 经过点
经过点 ,此时点
,此时点 的坐标为
的坐标为__________ .

 ,点B在第一象限.标记点B的位置后,将
,点B在第一象限.标记点B的位置后,将 沿x轴正方向平移至
沿x轴正方向平移至 的位置,使
的位置,使 经过点B,再标记点
经过点B,再标记点 的位置,继续平移至
的位置,继续平移至 的位置,使
的位置,使 经过点
经过点 ,此时点
,此时点 的坐标为
的坐标为
14.如图,在平面直角坐标系中,点 在抛物线
在抛物线 上,过点A作y轴的垂线,交抛物线于另一点B,点C、D在线段AB上,分别过点C、D作x轴的垂线交抛物线于E、F两点.当四边形CDFE为正方形时,线段CD的长为
上,过点A作y轴的垂线,交抛物线于另一点B,点C、D在线段AB上,分别过点C、D作x轴的垂线交抛物线于E、F两点.当四边形CDFE为正方形时,线段CD的长为_________ .

 在抛物线
在抛物线 上,过点A作y轴的垂线,交抛物线于另一点B,点C、D在线段AB上,分别过点C、D作x轴的垂线交抛物线于E、F两点.当四边形CDFE为正方形时,线段CD的长为
上,过点A作y轴的垂线,交抛物线于另一点B,点C、D在线段AB上,分别过点C、D作x轴的垂线交抛物线于E、F两点.当四边形CDFE为正方形时,线段CD的长为
15.先化简,再求值: ,其中
,其中 .
.
 ,其中
,其中 .
.16.在一个不透明的口袋中装有三个小球,分别标记数字1、2、3,每个小球除数字不同外其余均相同,小明和小亮玩摸球游戏,两人各摸一个球,谁摸到的数字大谁获胜,摸到相同数字记为平局.小明从口袋中摸出一个小球记下数字后放回并搅匀,小亮再从口袋中摸出一个小球.用画树状图(或列表)的方法,求小明获胜的概率.
17.为助力乡村发展,某购物平台推出有机大米促销活动,其中每千克有机大米的售价仅比普通大米多2元,用420元购买的有机大米与用300元购买的普通大米的重量相同,求每千克有机大米的售价为多少元?
18.如图,在菱形ABCD中,对角线AC与BD相交于点O, ,
, ,点E在边AD上,
,点E在边AD上, ,连结BE交AC于点M.
,连结BE交AC于点M.

(1)求AM的长.
(2) 的值为 .
的值为 .
 ,
, ,点E在边AD上,
,点E在边AD上, ,连结BE交AC于点M.
,连结BE交AC于点M.
(1)求AM的长.
(2)
 的值为 .
的值为 .19.稳定的粮食产量是人民幸福生活的基本保障.为了解粮食产量情况,小明查阅相关资料得到如下信息:长春市2020年的粮食总产量达到960万吨,比上年增长约9%,其中玉米产量增长约12%,水稻产量下降约2%,其他农作物产量下降约10%.

(注:以上数据中粮食产量均精确到万吨)
根据以上信息回答下列问题:
(1)2020年玉米产量比2019年玉米产量多万吨.
(2)扇形统计图中n的值为 .
(3)计算2020年水稻的产量.
(4)小明发现如果这样计算2020年粮食总产量的年增长率: ,就与2020年粮食总产量比上年增长约9%不符.请说明原因.
,就与2020年粮食总产量比上年增长约9%不符.请说明原因.

(注:以上数据中粮食产量均精确到万吨)
根据以上信息回答下列问题:
(1)2020年玉米产量比2019年玉米产量多万吨.
(2)扇形统计图中n的值为 .
(3)计算2020年水稻的产量.
(4)小明发现如果这样计算2020年粮食总产量的年增长率:
 ,就与2020年粮食总产量比上年增长约9%不符.请说明原因.
,就与2020年粮食总产量比上年增长约9%不符.请说明原因.20.图①、图②、图③均是 的正方形网格,每个小正方形的边长均为1.每个小正方形的顶点称为格点,点A、B、C均为格点,只用无刻度的直尺,分别在给定的网格中找一格点M,按下列要求作图:
的正方形网格,每个小正方形的边长均为1.每个小正方形的顶点称为格点,点A、B、C均为格点,只用无刻度的直尺,分别在给定的网格中找一格点M,按下列要求作图:
(1)在图①中,连结MA、MB,使 .
.
(2)在图②中,连结MA、MB、MC,使 .
.
(3)在图③中,连结MA、MC,使 .
.

 的正方形网格,每个小正方形的边长均为1.每个小正方形的顶点称为格点,点A、B、C均为格点,只用无刻度的直尺,分别在给定的网格中找一格点M,按下列要求作图:
的正方形网格,每个小正方形的边长均为1.每个小正方形的顶点称为格点,点A、B、C均为格点,只用无刻度的直尺,分别在给定的网格中找一格点M,按下列要求作图:(1)在图①中,连结MA、MB,使
 .
.(2)在图②中,连结MA、MB、MC,使
 .
.(3)在图③中,连结MA、MC,使
 .
.
21.《九章算术》中记载,浮箭漏(图①)出现于汉武帝时期,它由供水壶和箭壶组成,箭壶内装有箭尺,水匀速地从供水查流到箭壶,箭壶中的水位逐渐上升,箭尺匀速上浮,可通过读取箭尺读数计算时间,某学校STEAM小组仿制了一套浮箭漏,并从函数角度进行了如下实验探究:
【实验观察】实验小组通过观察,每2小时记录次箭尺读数,得到下表:
【探索发现】(1)建立平面直角坐标系,如图②,横轴表示供水时间x.纵轴表示箭尺读数y,描出以表格中数据为坐标的各点.
(2)观察上述各点的分布规律,判断它们是否在同一条直线上,如果在同一条直线上,求出这条直线所对应的函数表达式,如果不在同一条直线上,说明理由.
【结论应用】应用上述发现的规律估算:
(3)供水时间达到12小时时,箭尺的读数为多少厘米?
(4)如果本次实验记录的开始时间是上午8:00,那么当箭尺读数为90厘米时是几点钟?(箭尺最大读数为100厘米)


【实验观察】实验小组通过观察,每2小时记录次箭尺读数,得到下表:
| 供水时间x(小时) | 0 | 2 | 4 | 6 | 8 |
| 箭尺读数y(厘米) | 6 | 18 | 30 | 42 | 54 |
(2)观察上述各点的分布规律,判断它们是否在同一条直线上,如果在同一条直线上,求出这条直线所对应的函数表达式,如果不在同一条直线上,说明理由.
【结论应用】应用上述发现的规律估算:
(3)供水时间达到12小时时,箭尺的读数为多少厘米?
(4)如果本次实验记录的开始时间是上午8:00,那么当箭尺读数为90厘米时是几点钟?(箭尺最大读数为100厘米)


22.实践与探究
操作一:如图①,已知正方形纸片ABCD,将正方形纸片沿过点A的直线折叠,使点B落在正方形ABCD的内部,点B的对应点为点M,折痕为AE,再将纸片沿过点A的直线折叠,使AD与AM重合,折痕为AF,则 度.
度.
操作二:如图②,将正方形纸片沿EF继续折叠,点C的对应点为点N.我们发现,当点E的位置不同时,点N的位置也不同.当点E在BC边的某一位置时,点N恰好落在折痕AE上,则 度.
度.
在图②中,运用以上操作所得结论,解答下列问题:
(1)设AM与NF的交点为点P.求证 :.
:.
(2)若 ,则线段AP的长为 .
,则线段AP的长为 .

操作一:如图①,已知正方形纸片ABCD,将正方形纸片沿过点A的直线折叠,使点B落在正方形ABCD的内部,点B的对应点为点M,折痕为AE,再将纸片沿过点A的直线折叠,使AD与AM重合,折痕为AF,则
 度.
度.操作二:如图②,将正方形纸片沿EF继续折叠,点C的对应点为点N.我们发现,当点E的位置不同时,点N的位置也不同.当点E在BC边的某一位置时,点N恰好落在折痕AE上,则
 度.
度.在图②中,运用以上操作所得结论,解答下列问题:
(1)设AM与NF的交点为点P.求证
 :.
:.(2)若
 ,则线段AP的长为 .
,则线段AP的长为 .
23.如图,在 中,
中, ,
, ,
, ,点D为边AC的中点.动点P从点A出发,沿折线AB—BC以每秒1个单位长度的速度向点C运动,当点P不与点A、C重合时,连结PD.作点A关于直线PD的对称点
,点D为边AC的中点.动点P从点A出发,沿折线AB—BC以每秒1个单位长度的速度向点C运动,当点P不与点A、C重合时,连结PD.作点A关于直线PD的对称点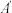 ,连结
,连结 、
、 .设点P的运动时间为t秒.
.设点P的运动时间为t秒.
(1)线段AD的长为 .
(2)用含t的代数式表示线段BP的长.
(3)当点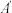 在
在 内部时,求
内部时,求 的取值范围.
的取值范围.
(4)当 与
与 相等时,直接写出
相等时,直接写出 的值.
的值.

 中,
中, ,
, ,
, ,点D为边AC的中点.动点P从点A出发,沿折线AB—BC以每秒1个单位长度的速度向点C运动,当点P不与点A、C重合时,连结PD.作点A关于直线PD的对称点
,点D为边AC的中点.动点P从点A出发,沿折线AB—BC以每秒1个单位长度的速度向点C运动,当点P不与点A、C重合时,连结PD.作点A关于直线PD的对称点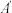 ,连结
,连结 、
、 .设点P的运动时间为t秒.
.设点P的运动时间为t秒.(1)线段AD的长为 .
(2)用含t的代数式表示线段BP的长.
(3)当点
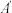 在
在 内部时,求
内部时,求 的取值范围.
的取值范围.(4)当
 与
与 相等时,直接写出
相等时,直接写出 的值.
的值.
24.在平面直角坐标系中,抛物线 (m为常数)的顶点为A.
(m为常数)的顶点为A.
(1)当 时,点A的坐标是 ,抛物线与y轴交点的坐标是 .
时,点A的坐标是 ,抛物线与y轴交点的坐标是 .
(2)若点A在第一象限,且 ,求此抛物线所对应的二次函数的表达式,并写出函数值y随x的增大而减小时x的取值范围.
,求此抛物线所对应的二次函数的表达式,并写出函数值y随x的增大而减小时x的取值范围.
(3)当 时,若函数
时,若函数 的最小值为3,求m的值.
的最小值为3,求m的值.
(4)分别过点 、
、 作y轴的垂线,交抛物线的对称轴于点M、N.当抛物线
作y轴的垂线,交抛物线的对称轴于点M、N.当抛物线 与四边形PQNM的边有两个交点时,将这两个交点分别记为点B、点C,且点B的纵坐标大于点C的纵坐标.若点B到y轴的距离与点C到x轴的距离相等,直接写出m的值.
与四边形PQNM的边有两个交点时,将这两个交点分别记为点B、点C,且点B的纵坐标大于点C的纵坐标.若点B到y轴的距离与点C到x轴的距离相等,直接写出m的值.

 (m为常数)的顶点为A.
(m为常数)的顶点为A.(1)当
 时,点A的坐标是 ,抛物线与y轴交点的坐标是 .
时,点A的坐标是 ,抛物线与y轴交点的坐标是 .(2)若点A在第一象限,且
 ,求此抛物线所对应的二次函数的表达式,并写出函数值y随x的增大而减小时x的取值范围.
,求此抛物线所对应的二次函数的表达式,并写出函数值y随x的增大而减小时x的取值范围.(3)当
 时,若函数
时,若函数 的最小值为3,求m的值.
的最小值为3,求m的值.(4)分别过点
 、
、 作y轴的垂线,交抛物线的对称轴于点M、N.当抛物线
作y轴的垂线,交抛物线的对称轴于点M、N.当抛物线 与四边形PQNM的边有两个交点时,将这两个交点分别记为点B、点C,且点B的纵坐标大于点C的纵坐标.若点B到y轴的距离与点C到x轴的距离相等,直接写出m的值.
与四边形PQNM的边有两个交点时,将这两个交点分别记为点B、点C,且点B的纵坐标大于点C的纵坐标.若点B到y轴的距离与点C到x轴的距离相等,直接写出m的值.
 搜索
搜索
 难度系数:0.94
难度系数:0.94  答案解析
答案解析
 有奖纠错
有奖纠错
