全一卷
1.实数2021的相反数是( )
| A.2021 | B. | C. | D. |
2.下列运算正确的是( )
A. | B. | C. | D. |
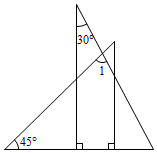
3.将一副直角三角板按如图所示的方式放置,使用 角的三角板的直角边和含
角的三角板的直角边和含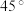 角的三角板的直角边垂直,则∠1的度数为( )
角的三角板的直角边垂直,则∠1的度数为( )
 角的三角板的直角边和含
角的三角板的直角边和含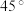 角的三角板的直角边垂直,则∠1的度数为( )
角的三角板的直角边垂直,则∠1的度数为( )
A.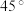 | B. | C. | D. |
4.一只不透明的袋子中装有3个黑球和2个白球,这些除颜色外无其他差别,从中任意摸出3个球,下列事件是必然事件的为( )
| A.至少有1个球是黑球 | B.至少有1个球是白球 |
| C.至少有2个球是黑球 | D.至少有2个球是白球 |
5.由4个棱长均为1的小正方形组成如图所示的几何体,这个几何体的表面积为( )


| A.18 | B.15 | C.12 | D.6 |
6.若关于 的一元二次方程
的一元二次方程 的一个根是2,则
的一个根是2,则 的值为( )
的值为( )
 的一元二次方程
的一元二次方程 的一个根是2,则
的一个根是2,则 的值为( )
的值为( )| A.2 | B.3 | C.4 | D.5 |
7.如图,抛物线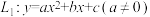 与
与 轴只有一个公共点A(1,0),与
轴只有一个公共点A(1,0),与 轴交于点B(0,2),虚线为其对称轴,若将抛物线向下平移两个单位长度得抛物线
轴交于点B(0,2),虚线为其对称轴,若将抛物线向下平移两个单位长度得抛物线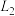 ,则图中两个阴影部分的面积和为( )
,则图中两个阴影部分的面积和为( )
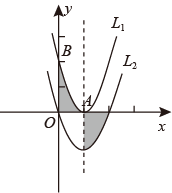
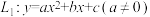 与
与 轴只有一个公共点A(1,0),与
轴只有一个公共点A(1,0),与 轴交于点B(0,2),虚线为其对称轴,若将抛物线向下平移两个单位长度得抛物线
轴交于点B(0,2),虚线为其对称轴,若将抛物线向下平移两个单位长度得抛物线 ,则图中两个阴影部分的面积和为( )
,则图中两个阴影部分的面积和为( )
| A.1 | B.2 | C.3 | D.4 |
8.如图,在Rt△ACB中,∠ACB=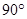 ,AC=6,BC=8,若以AC为直径的☉O交AB于点D,则CD的长为( )
,AC=6,BC=8,若以AC为直径的☉O交AB于点D,则CD的长为( )
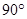 ,AC=6,BC=8,若以AC为直径的☉O交AB于点D,则CD的长为( )
,AC=6,BC=8,若以AC为直径的☉O交AB于点D,则CD的长为( )
A. | B. | C. | D.5 |
9.已知直线 与
与 轴、
轴、 轴分别交于A、B两点,点P是第一象限内的点,若△PAB为等腰直角三角形,则点P的坐标为( )
轴分别交于A、B两点,点P是第一象限内的点,若△PAB为等腰直角三角形,则点P的坐标为( )
 与
与 轴、
轴、 轴分别交于A、B两点,点P是第一象限内的点,若△PAB为等腰直角三角形,则点P的坐标为( )
轴分别交于A、B两点,点P是第一象限内的点,若△PAB为等腰直角三角形,则点P的坐标为( )| A.(1,1) |
| B.(1,1)或(1,2) |
| C.(1,1)或(1,2)或(2,1) |
| D.(0,0)或(1,1)或(1,2)或(2,1) |
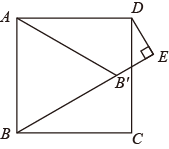
10.如图,在边长为2的正方形ABCD中,若将AB绕点A逆时针旋转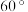 ,使点B落在点
,使点B落在点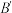 的位置,连接B
的位置,连接B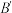 ,过点D作DE⊥
,过点D作DE⊥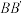 ,交
,交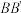 的延长线于点E,则
的延长线于点E,则 的长为( )
的长为( )
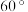 ,使点B落在点
,使点B落在点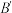 的位置,连接B
的位置,连接B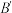 ,过点D作DE⊥
,过点D作DE⊥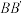 ,交
,交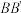 的延长线于点E,则
的延长线于点E,则 的长为( )
的长为( )
A. | B. | C. | D. |
11.目前我国建成世界上规模最大的社会保障体系,截止2020年12月底,基本医疗保险覆盖超过13亿人,覆盖94.6%以上的人口.在这里,1300000000用科学记数法表示为 __________ .
12.分解因式:
___________ .

13.黔东南州某校今年春季开展体操活动,小聪收集、整理了成绩突出的甲、乙两队队员(各50名)的身高得到:平均身高(单位:cm)分别为: =160,
=160, ,方差分别为:
,方差分别为: ,
, ,现要从甲、乙两队中选出身高比较整齐的一个队参加上一级的体操比赛,根据上述数据,应该选择
,现要从甲、乙两队中选出身高比较整齐的一个队参加上一级的体操比赛,根据上述数据,应该选择_________ .(填写“甲队”或“乙队”)
 =160,
=160, ,方差分别为:
,方差分别为: ,
, ,现要从甲、乙两队中选出身高比较整齐的一个队参加上一级的体操比赛,根据上述数据,应该选择
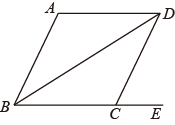
,现要从甲、乙两队中选出身高比较整齐的一个队参加上一级的体操比赛,根据上述数据,应该选择14.如图,BD是菱形ABCD的一条对角线,点E在BC的延长线上,若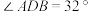 ,则
,则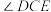 的度数为
的度数为_________ 度.
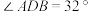 ,则
,则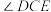 的度数为
的度数为
15.已知在平面直角坐标系中,△AOB的顶点分别为点A(2,1)、点B(2,0)、点O(0,0),若以原点O为位似中心,相似比为2,将△AOB放大,则点A的对应点的坐标为________ .
16.不等式组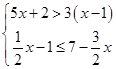 的解集是
的解集是__________ .
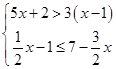 的解集是
的解集是17.小明很喜欢钻研问题,一次数学杨老师拿来一个残缺的圆形瓦片(如图所示)让小明求瓦片所在园的半径,小明连接瓦片弧线两端AB,量的弧AB的中心C到AB的距离CD=1.6cm,AB=6.4cm,很快求得圆形瓦片所在圆的半径为 _________ cm.


18.如图,要用一个扇形纸片围成一个无底盖的圆锥(接缝处忽略不计),若该圆锥的底面圆周长为 cm,侧面积为
cm,侧面积为
 ,则这个扇形的圆心角的度数是
,则这个扇形的圆心角的度数是__________ 度.

 cm,侧面积为
cm,侧面积为
 ,则这个扇形的圆心角的度数是
,则这个扇形的圆心角的度数是
19.如图,若反比例函数 的图像经过等边三角形POQ的顶点P,则△POQ的边长为
的图像经过等边三角形POQ的顶点P,则△POQ的边长为____________ .

 的图像经过等边三角形POQ的顶点P,则△POQ的边长为
的图像经过等边三角形POQ的顶点P,则△POQ的边长为
20.如图,二次函数 的函数图像经过点(1,2),且与
的函数图像经过点(1,2),且与 轴交点的横坐标分别为
轴交点的横坐标分别为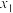 、
、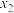 ,其中 -1<
,其中 -1<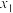 <0,1<
<0,1<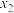 <2,下列结论:①
<2,下列结论:①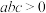 ;②
;② ;③
;③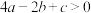 ;④当
;④当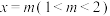 时,
时,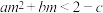 ;⑤
;⑤ ,其中正确的有
,其中正确的有 ___________ .(填写正确的序号)

 的函数图像经过点(1,2),且与
的函数图像经过点(1,2),且与 轴交点的横坐标分别为
轴交点的横坐标分别为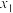 、
、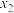 ,其中 -1<
,其中 -1<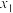 <0,1<
<0,1<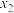 <2,下列结论:①
<2,下列结论:①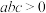 ;②
;② ;③
;③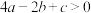 ;④当
;④当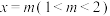 时,
时,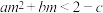 ;⑤
;⑤ ,其中正确的有
,其中正确的有 
21.(1)计算:
(2)先化简: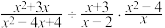 ,然后
,然后 从0、1、2三个数中选一个你认为合适的数代入求值.
从0、1、2三个数中选一个你认为合适的数代入求值.

(2)先化简:
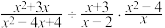 ,然后
,然后 从0、1、2三个数中选一个你认为合适的数代入求值.
从0、1、2三个数中选一个你认为合适的数代入求值.22.为庆祝中国共产党建党100周年,某校开展了“党在我心中”党史知识竞赛,竞赛得分为整数,王老师为了解竞赛情况,随机抽取了部分参赛学生的得分并进行整理,绘制成如下不完整的统计图表:
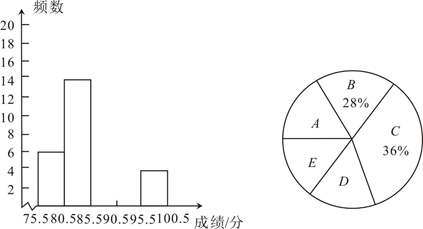
请你根据上面的统计图表提供的信息解答下列问题:
(1)上表中的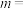 ,
, ,
,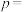 .
.
(2)这次抽样调查的成绩的中位数落在哪个组?请补全频数分布直方图.
(3)已知该校有1000名学生参赛,请估计竞赛成绩在90分以上(不含90分)的学生有多少人?
(4)现要从E组随机抽取两名学生参加上级部门组织的党史知识竞赛,E组中的小丽和小洁是一对好朋友,请用列表或画树状图的方法求出恰好抽到小丽和小洁的概率.

| 组别 | 成绩 (分) (分) | 频数 |
| A | 75.5 | 6 |
| B |  | 14 |
| C |  |  |
| D |  |  |
| E |  | 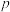 |
请你根据上面的统计图表提供的信息解答下列问题:
(1)上表中的
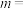 ,
, ,
,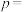 .
.(2)这次抽样调查的成绩的中位数落在哪个组?请补全频数分布直方图.
(3)已知该校有1000名学生参赛,请估计竞赛成绩在90分以上(不含90分)的学生有多少人?
(4)现要从E组随机抽取两名学生参加上级部门组织的党史知识竞赛,E组中的小丽和小洁是一对好朋友,请用列表或画树状图的方法求出恰好抽到小丽和小洁的概率.
23.如图,PA是以AC为直径的☉O的切线,切点为A,过点A作AB⊥OP,交☉O于点B.

(1)求证:PB是☉O的切线;
(2)若AB=6,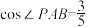 ,求PO的长.
,求PO的长.

(1)求证:PB是☉O的切线;
(2)若AB=6,
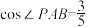 ,求PO的长.
,求PO的长.24.黔东南州某销售公司准备购进A、B两种商品,已知购进3件A商品和2件B商品,需要1100元;购进5件A商品和3件B商品,需要1750元.
(1)求A、B两种商品的进货单价分别是多少元?
(2)若该公司购进A商品200件,B商品300件,准备把这些商品全部运往甲、乙两地销售.已知每件A商品运往甲、乙两地的运费分别为20元和25元;每件B商品运往甲、乙两地的运费分别为15元和24元.若运往甲地的商品共240件,运往乙地的商品共260件.
①设运往甲地的A商品为 (件),投资总运费为
(件),投资总运费为 (元),请写出
(元),请写出 与
与 的函数关系式;
的函数关系式;
②怎样调运A、B两种商品可使投资总费用最少?最少费用是多少元?(投资总费用=购进商品的费用+运费)
(1)求A、B两种商品的进货单价分别是多少元?
(2)若该公司购进A商品200件,B商品300件,准备把这些商品全部运往甲、乙两地销售.已知每件A商品运往甲、乙两地的运费分别为20元和25元;每件B商品运往甲、乙两地的运费分别为15元和24元.若运往甲地的商品共240件,运往乙地的商品共260件.
①设运往甲地的A商品为
 (件),投资总运费为
(件),投资总运费为 (元),请写出
(元),请写出 与
与 的函数关系式;
的函数关系式;②怎样调运A、B两种商品可使投资总费用最少?最少费用是多少元?(投资总费用=购进商品的费用+运费)
25.在四边形ABCD中,对角线AC平分∠BAD.


【探究发现】
(1)如图①,若∠BAD= ,∠ABC=∠ADC=
,∠ABC=∠ADC= .求证:AD+AB=AC;
.求证:AD+AB=AC;
【拓展迁移】
(2)如图②,若∠BAD= ,∠ABC+∠ADC=
,∠ABC+∠ADC= .
.
①猜想AB、AD、AC三条线段的数量关系,并说明理由;
②若AC=10,求四边形ABCD的面积.


【探究发现】
(1)如图①,若∠BAD=
 ,∠ABC=∠ADC=
,∠ABC=∠ADC= .求证:AD+AB=AC;
.求证:AD+AB=AC;【拓展迁移】
(2)如图②,若∠BAD=
 ,∠ABC+∠ADC=
,∠ABC+∠ADC= .
.①猜想AB、AD、AC三条线段的数量关系,并说明理由;
②若AC=10,求四边形ABCD的面积.
26.图,抛物线 与
与 轴交于A、B(3,0)两点,与
轴交于A、B(3,0)两点,与 轴交于点C(0,-3),抛物线的顶点为D.
轴交于点C(0,-3),抛物线的顶点为D.
(1)求抛物线的解析式;
(2)点P在抛物线的对称轴上,点Q在 轴上,若以点P、Q、B、C为顶点,BC为边的四边形为平行四边形,请直接写出点P、Q的坐标;
轴上,若以点P、Q、B、C为顶点,BC为边的四边形为平行四边形,请直接写出点P、Q的坐标;
(3)已知点M是 轴上的动点,过点M作
轴上的动点,过点M作 的垂线交抛物线于点G,是否存在这样的点M,使得以点A、M、G为顶点的三角形与△BCD相似,若存在,请求出点M的坐标;若不存在,请说明理由.
的垂线交抛物线于点G,是否存在这样的点M,使得以点A、M、G为顶点的三角形与△BCD相似,若存在,请求出点M的坐标;若不存在,请说明理由.

 与
与 轴交于A、B(3,0)两点,与
轴交于A、B(3,0)两点,与 轴交于点C(0,-3),抛物线的顶点为D.
轴交于点C(0,-3),抛物线的顶点为D.(1)求抛物线的解析式;
(2)点P在抛物线的对称轴上,点Q在
 轴上,若以点P、Q、B、C为顶点,BC为边的四边形为平行四边形,请直接写出点P、Q的坐标;
轴上,若以点P、Q、B、C为顶点,BC为边的四边形为平行四边形,请直接写出点P、Q的坐标;(3)已知点M是
 轴上的动点,过点M作
轴上的动点,过点M作 的垂线交抛物线于点G,是否存在这样的点M,使得以点A、M、G为顶点的三角形与△BCD相似,若存在,请求出点M的坐标;若不存在,请说明理由.
的垂线交抛物线于点G,是否存在这样的点M,使得以点A、M、G为顶点的三角形与△BCD相似,若存在,请求出点M的坐标;若不存在,请说明理由.
 搜索
搜索
 难度系数:0.85
难度系数:0.85  答案解析
答案解析
 有奖纠错
有奖纠错
