全一卷
1.-5的绝对值等于( )
| A.-5 | B.5 | C. | D.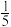 |
2.下面计算正确的是( )
A. | B. |
C. | D. |
3.如图所示,该几何体的俯视图为( )


A. | B. | C. | D. |
4.在函数 中,自变量
中,自变量 的取值范围是( )
的取值范围是( )
 中,自变量
中,自变量 的取值范围是( )
的取值范围是( )A. | B. | C. | D. |
5.四张背面完全相同的卡片,正面分别印有等腰三角形、圆、平行四边形、正六边形,现在把它们的正面向下,随机的摆放在桌面上,从中任意抽出一张,则抽到的卡片正面是中心对称图形的概率是( )
A. | B. | C. | D.1 |
6.如图, 是
是 的角平分线,过点
的角平分线,过点 作
作 交
交 延长线于点
延长线于点 ,若
,若 ,
, ,则
,则 的度数为( )
的度数为( )

 是
是 的角平分线,过点
的角平分线,过点 作
作 交
交 延长线于点
延长线于点 ,若
,若 ,
, ,则
,则 的度数为( )
的度数为( )
| A.100° | B.110° | C.125° | D.135° |
7.如图,在四边形 中,
中, ,
, ,
, ,
, ,分别以
,分别以 和
和 为圆心,以大于
为圆心,以大于 的长为半径作弧,两弧相交于点
的长为半径作弧,两弧相交于点 和
和 ,直线
,直线 与
与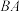 延长线交于点
延长线交于点 ,连接
,连接 ,则
,则 的内切圆半径是( )
的内切圆半径是( )

 中,
中, ,
, ,
, ,
, ,分别以
,分别以 和
和 为圆心,以大于
为圆心,以大于 的长为半径作弧,两弧相交于点
的长为半径作弧,两弧相交于点 和
和 ,直线
,直线 与
与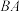 延长线交于点
延长线交于点 ,连接
,连接 ,则
,则 的内切圆半径是( )
的内切圆半径是( )
| A.4 | B. | C.2 | D.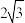 |
8.如图,二次函数 (
( )的图象与
)的图象与 轴交于
轴交于 ,
, 两点,与
两点,与 轴交于点
轴交于点 ,点
,点 坐标为
坐标为 ,点
,点 在
在 与
与 之间(不包括这两点),抛物线的顶点为
之间(不包括这两点),抛物线的顶点为 ,对称轴为直线
,对称轴为直线 ,有以下结论:①
,有以下结论:① ;②若点
;②若点 ,点
,点 是函数图象上的两点,则
是函数图象上的两点,则 ;③
;③ ;④
;④ 可以是等腰直角三形.其中正确的有( )
可以是等腰直角三形.其中正确的有( )

 (
( )的图象与
)的图象与 轴交于
轴交于 ,
, 两点,与
两点,与 轴交于点
轴交于点 ,点
,点 坐标为
坐标为 ,点
,点 在
在 与
与 之间(不包括这两点),抛物线的顶点为
之间(不包括这两点),抛物线的顶点为 ,对称轴为直线
,对称轴为直线 ,有以下结论:①
,有以下结论:① ;②若点
;②若点 ,点
,点 是函数图象上的两点,则
是函数图象上的两点,则 ;③
;③ ;④
;④ 可以是等腰直角三形.其中正确的有( )
可以是等腰直角三形.其中正确的有( )
| A.1个 | B.2个 | C.3个 | D.4个 |
9.据有关报道,2020年某市斥资约5 800 000元改造老旧小区,数据5 800 000科学记数法表示为_________ .
10.因式分解:
_________ .

11.一次函数 ,且
,且 ,则它的图象不经过第
,则它的图象不经过第_________ 象限.
 ,且
,且 ,则它的图象不经过第
,则它的图象不经过第12.甲、乙两人进行飞镖比赛,每人投5次,所得平均环数相等,其中甲所得环数的方差为5,乙所得环数如下:2,3,5,7,8,那么成绩较稳定的是_________ (填“甲”或“乙”).
13.关于 的方程
的方程 有两个实数根,则
有两个实数根,则 的取值范围是
的取值范围是_________ .
 的方程
的方程 有两个实数根,则
有两个实数根,则 的取值范围是
的取值范围是14.如图,矩形 的边
的边 在
在 轴上,点
轴上,点 在反比例函数
在反比例函数 的图象上,点
的图象上,点 在反比例函数
在反比例函数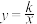 的图象上,若
的图象上,若 ,
, ,则
,则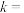
_________ .

 的边
的边 在
在 轴上,点
轴上,点 在反比例函数
在反比例函数 的图象上,点
的图象上,点 在反比例函数
在反比例函数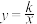 的图象上,若
的图象上,若 ,
, ,则
,则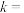

15.如图,在四边形 中,
中, ,
, ,
, ,
, ,点
,点 和点
和点 分别是
分别是 和
和 的中点,连接
的中点,连接 ,
, ,
, ,若
,若 ,则
,则 的面积是
的面积是_________ .

 中,
中, ,
, ,
, ,
, ,点
,点 和点
和点 分别是
分别是 和
和 的中点,连接
的中点,连接 ,
, ,
, ,若
,若 ,则
,则 的面积是
的面积是
16.如图,在矩形 中,
中, ,
, ,连接
,连接 ,以
,以 为边,作矩形
为边,作矩形 使
使 ,连接
,连接 交
交 于点
于点 ;以
;以 为边,作矩形
为边,作矩形 ,使
,使 ,连接
,连接 交
交 于点
于点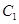 ;以
;以 为边,作矩形
为边,作矩形 ,使
,使 ,连接
,连接 交
交 于点
于点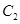 ;…按照这个规律进行下去,则
;…按照这个规律进行下去,则 的面积为_________.
的面积为_________.

 中,
中, ,
, ,连接
,连接 ,以
,以 为边,作矩形
为边,作矩形 使
使 ,连接
,连接 交
交 于点
于点 ;以
;以 为边,作矩形
为边,作矩形 ,使
,使 ,连接
,连接 交
交 于点
于点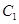 ;以
;以 为边,作矩形
为边,作矩形 ,使
,使 ,连接
,连接 交
交 于点
于点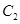 ;…按照这个规律进行下去,则
;…按照这个规律进行下去,则 的面积为_________.
的面积为_________.
17.先化简,再求代数式的值: ,其中
,其中 .
.
 ,其中
,其中 .
.18.如图,在平面直角坐标系中,网格的每个小方格都是边长为1个单位长度的正方形,点 ,
, ,
, 的坐标分别为
的坐标分别为 ,
, ,
, ,先以原点
,先以原点 为位似中心在第三象限内画一个
为位似中心在第三象限内画一个 ,使它与
,使它与 位似,且相似比为2:1,然后再把
位似,且相似比为2:1,然后再把 绕原点
绕原点 逆时针旋转90°得到
逆时针旋转90°得到 .
.

(1)画出 ,并直接写出点
,并直接写出点 的坐标;
的坐标;
(2)画出 ,直接写出在旋转过程中,点
,直接写出在旋转过程中,点 到点
到点 所经过的路径长.
所经过的路径长.
 ,
, ,
, 的坐标分别为
的坐标分别为 ,
, ,
, ,先以原点
,先以原点 为位似中心在第三象限内画一个
为位似中心在第三象限内画一个 ,使它与
,使它与 位似,且相似比为2:1,然后再把
位似,且相似比为2:1,然后再把 绕原点
绕原点 逆时针旋转90°得到
逆时针旋转90°得到 .
.
(1)画出
 ,并直接写出点
,并直接写出点 的坐标;
的坐标;(2)画出
 ,直接写出在旋转过程中,点
,直接写出在旋转过程中,点 到点
到点 所经过的路径长.
所经过的路径长.19.某校为了解疫情期间学生居家学习情况,以问卷调查的形式随机调查了部分学生居家学习的主要方式(每名学生只选最主要的一种),并将调查结果绘制成如下不完整的统计图.


根据以上信息回答下列问题:
(1)参与本次问卷调查的学生共有_________人,其中选择 类型的有_________人;
类型的有_________人;
(2)在扇形统计图中,求 所对应的圆心角度数,并补全条形统计图;
所对应的圆心角度数,并补全条形统计图;
(3)该校学生人数为1250人,选择 、
、 、
、 三种学习方式大约共有多少人?
三种学习方式大约共有多少人?
种类 |
|
|
|
|
|
学习方式 | 老师直播 教学课程 | 国家教育云平台 教学课程 | 电视台播放 教学课程 | 第三方 网上课程 | 其他 |


根据以上信息回答下列问题:
(1)参与本次问卷调查的学生共有_________人,其中选择
 类型的有_________人;
类型的有_________人;(2)在扇形统计图中,求
 所对应的圆心角度数,并补全条形统计图;
所对应的圆心角度数,并补全条形统计图;(3)该校学生人数为1250人,选择
 、
、 、
、 三种学习方式大约共有多少人?
三种学习方式大约共有多少人?20.在一个不透明的口袋中装有4个依次写有数字1,2,3,4的小球,它们除数字外都相同,每次摸球前都将小球摇匀.
(1)从中随机摸出一个小球,小球上写的数字不大于3的概率是_________;
(2)若从中随机摸出一球不放回,再随机摸出一球,请用画树状图或列表的方法,求两次摸出小球上的数字和 恰好是偶数的概率.
(1)从中随机摸出一个小球,小球上写的数字不大于3的概率是_________;
(2)若从中随机摸出一球不放回,再随机摸出一球,请用画树状图或列表的方法,求两次摸出小球上的
21.为帮助贫困山区孩子学习,某学校号召学生自愿捐书,已知七、八年级同学捐书总数都是1800本,八年级捐书人数比七年级多150人,七年级人均捐书数量是八年级人均捐书数量的1.5倍,求八年级捐书人数是多少?
22.如图,已知 ,以
,以 为直径的
为直径的 交
交 于点
于点 ,连接
,连接 ,
, 的平分线交
的平分线交 于点
于点 ,交
,交 于点
于点 ,且
,且 .
.

(1)判断 所在直线与
所在直线与 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)若 ,
, ,求
,求 的半径.
的半径.
 ,以
,以 为直径的
为直径的 交
交 于点
于点 ,连接
,连接 ,
, 的平分线交
的平分线交 于点
于点 ,交
,交 于点
于点 ,且
,且 .
.
(1)判断
 所在直线与
所在直线与 的位置关系,并说明理由;
的位置关系,并说明理由;(2)若
 ,
, ,求
,求 的半径.
的半径.23.如图,小岛 和
和 都在码头
都在码头 的正北方向上,它们之间距离为
的正北方向上,它们之间距离为 ,一艘渔船自西向东匀速航行,行驶到位于码头
,一艘渔船自西向东匀速航行,行驶到位于码头 的正西方向
的正西方向 处时,测得
处时,测得 ,渔船速度为
,渔船速度为 ,经过
,经过 ,渔船行驶到了
,渔船行驶到了 处,测得
处,测得 ,求渔船在
,求渔船在 处时距离码头
处时距离码头 有多远?(结果精确到
有多远?(结果精确到 )
)
(参考数据: ,
, ,
, ,
, ,
, ,
, )
)

 和
和 都在码头
都在码头 的正北方向上,它们之间距离为
的正北方向上,它们之间距离为 ,一艘渔船自西向东匀速航行,行驶到位于码头
,一艘渔船自西向东匀速航行,行驶到位于码头 的正西方向
的正西方向 处时,测得
处时,测得 ,渔船速度为
,渔船速度为 ,经过
,经过 ,渔船行驶到了
,渔船行驶到了 处,测得
处,测得 ,求渔船在
,求渔船在 处时距离码头
处时距离码头 有多远?(结果精确到
有多远?(结果精确到 )
)(参考数据:
 ,
, ,
, ,
, ,
, ,
, )
)
24.某服装批发市场销售一种衬衫,衬衫每件进货价为50元,规定每件售价不低于进货价,经市场调查,每月的销售量 (件)与每件的售价
(件)与每件的售价 (元)满足一次函数关系,部分数据如下表:
(元)满足一次函数关系,部分数据如下表:
(1)求出 与
与 之间的函数表达式;(不需要求自变量
之间的函数表达式;(不需要求自变量 的取值范围)
的取值范围)
(2)该批发市场每月想从这种衬衫销售中获利24000元,又想尽量给客户实惠,该如何给这种衬衫定价?
(3)物价部门规定,该衬衫的每件利润不允许高于进货价的30%,设这种衬衫每月的总利润为 (元),那么售价定为多少元可获得最大利润?最大利润是多少?
(元),那么售价定为多少元可获得最大利润?最大利润是多少?
 (件)与每件的售价
(件)与每件的售价 (元)满足一次函数关系,部分数据如下表:
(元)满足一次函数关系,部分数据如下表:售价 | 60 | 65 | 70 |
销售量 | 1400 | 1300 | 1200 |
 与
与 之间的函数表达式;(不需要求自变量
之间的函数表达式;(不需要求自变量 的取值范围)
的取值范围)(2)该批发市场每月想从这种衬衫销售中获利24000元,又想尽量给客户实惠,该如何给这种衬衫定价?
(3)物价部门规定,该衬衫的每件利润不允许高于进货价的30%,设这种衬衫每月的总利润为
 (元),那么售价定为多少元可获得最大利润?最大利润是多少?
(元),那么售价定为多少元可获得最大利润?最大利润是多少?25.已知:菱形 和菱形
和菱形 ,
, ,起始位置点
,起始位置点 在边
在边 上,点
上,点 在
在 所在直线上,点
所在直线上,点 在点
在点 的右侧,点
的右侧,点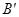 在点
在点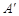 的右侧,连接
的右侧,连接 和
和 ,将菱形
,将菱形 以
以 为旋转中心逆时针旋转
为旋转中心逆时针旋转 角(
角( ).
).
(1)如图1,若点 与
与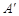 重合,且
重合,且 ,求证:
,求证: ;
;

(2)若点 与
与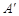 不重合,
不重合, 是
是 上一点,当
上一点,当 时,连接
时,连接 和
和 ,
, 和
和 所在直线相交于点
所在直线相交于点 ;
;
①如图2,当 时,请猜想线段
时,请猜想线段 和线段
和线段 的数量关系及
的数量关系及 的度数;
的度数;

②如图3,当 时,请求出线段
时,请求出线段 和线段
和线段 的数量关系及
的数量关系及 的度数;
的度数;

③在②的条件下,若点 与
与 的中点重合,
的中点重合, ,
,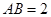 ,在整个旋转过程中,当点
,在整个旋转过程中,当点 与点
与点 重合时,请直接写出线段
重合时,请直接写出线段 的长.
的长.
 和菱形
和菱形 ,
, ,起始位置点
,起始位置点 在边
在边 上,点
上,点 在
在 所在直线上,点
所在直线上,点 在点
在点 的右侧,点
的右侧,点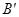 在点
在点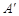 的右侧,连接
的右侧,连接 和
和 ,将菱形
,将菱形 以
以 为旋转中心逆时针旋转
为旋转中心逆时针旋转 角(
角( ).
).(1)如图1,若点
 与
与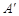 重合,且
重合,且 ,求证:
,求证: ;
;
(2)若点
 与
与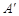 不重合,
不重合, 是
是 上一点,当
上一点,当 时,连接
时,连接 和
和 ,
, 和
和 所在直线相交于点
所在直线相交于点 ;
;①如图2,当
 时,请猜想线段
时,请猜想线段 和线段
和线段 的数量关系及
的数量关系及 的度数;
的度数;
②如图3,当
 时,请求出线段
时,请求出线段 和线段
和线段 的数量关系及
的数量关系及 的度数;
的度数;
③在②的条件下,若点
 与
与 的中点重合,
的中点重合, ,
,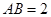 ,在整个旋转过程中,当点
,在整个旋转过程中,当点 与点
与点 重合时,请直接写出线段
重合时,请直接写出线段 的长.
的长.26.如图1,在平面直角坐标系中,抛物线 与
与 轴交于
轴交于 ,
, 两点,
两点, 点坐标为
点坐标为 ,与
,与 轴交于点
轴交于点 ,直线
,直线 与抛物线交于
与抛物线交于 ,
, 两点.
两点.

(1)求抛物线的函数表达式;
(2)求 的值和
的值和 点坐标;
点坐标;
(3)点 是直线
是直线 上方抛物线上的动点,过点
上方抛物线上的动点,过点 作
作 轴的垂线,垂足为
轴的垂线,垂足为 ,交直线
,交直线 于点
于点 ,过点
,过点 作
作 轴的平行线,交
轴的平行线,交 于点
于点 ,当
,当 是线段
是线段 的三等分点时,求
的三等分点时,求 点坐标;
点坐标;
(4)如图2, 是
是 轴上一点,其坐标为
轴上一点,其坐标为 ,动点
,动点 从
从 出发,沿
出发,沿 轴正方向以每秒5个单位的速度运动,设
轴正方向以每秒5个单位的速度运动,设 的运动时间为
的运动时间为 (
( ),连接
),连接 ,过
,过 作
作 于点
于点 ,以
,以 所在直线为对称轴,线段
所在直线为对称轴,线段 经轴对称变换后的图形为
经轴对称变换后的图形为 ,点
,点 在运动过程中,线段
在运动过程中,线段 的位置也随之变化,请直接写出运动过程中线段
的位置也随之变化,请直接写出运动过程中线段 与抛物线有公共点时
与抛物线有公共点时 的取值范围.
的取值范围.

 与
与 轴交于
轴交于 ,
, 两点,
两点, 点坐标为
点坐标为 ,与
,与 轴交于点
轴交于点 ,直线
,直线 与抛物线交于
与抛物线交于 ,
, 两点.
两点.
(1)求抛物线的函数表达式;
(2)求
 的值和
的值和 点坐标;
点坐标;(3)点
 是直线
是直线 上方抛物线上的动点,过点
上方抛物线上的动点,过点 作
作 轴的垂线,垂足为
轴的垂线,垂足为 ,交直线
,交直线 于点
于点 ,过点
,过点 作
作 轴的平行线,交
轴的平行线,交 于点
于点 ,当
,当 是线段
是线段 的三等分点时,求
的三等分点时,求 点坐标;
点坐标;(4)如图2,
 是
是 轴上一点,其坐标为
轴上一点,其坐标为 ,动点
,动点 从
从 出发,沿
出发,沿 轴正方向以每秒5个单位的速度运动,设
轴正方向以每秒5个单位的速度运动,设 的运动时间为
的运动时间为 (
( ),连接
),连接 ,过
,过 作
作 于点
于点 ,以
,以 所在直线为对称轴,线段
所在直线为对称轴,线段 经轴对称变换后的图形为
经轴对称变换后的图形为 ,点
,点 在运动过程中,线段
在运动过程中,线段 的位置也随之变化,请直接写出运动过程中线段
的位置也随之变化,请直接写出运动过程中线段 与抛物线有公共点时
与抛物线有公共点时 的取值范围.
的取值范围.
 搜索
搜索
 难度系数:0.94
难度系数:0.94  答案解析
答案解析
 有奖纠错
有奖纠错
