全一卷
1.|– |的倒数是( )
|的倒数是( )
 |的倒数是( )
|的倒数是( )| A.–2 | B.– | C. | D.2 |
2.已知某新型感冒病毒的直径约为0.000 000 733米,将0.000 000 733用科学记数法表示为( )
| A.7.33×10-6 | B.7.33×10-7 | C.7.33×106 | D.7.33×107 |
3.如图,一个几何体由5个大小相同、棱长为1的小正方体搭成,下列说法正确的是( ).


| A.主视图的面积为4 | B.左视图的面积为4 |
| C.俯视图的面积为3 | D.三种视图的面积都是4 |
4.关于 的不等式
的不等式 的解集为
的解集为 ,则
,则 的值为( )
的值为( )
 的不等式
的不等式 的解集为
的解集为 ,则
,则 的值为( )
的值为( )A. | B.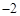 | C. | D. |
5.如图,在 中,将
中,将 沿AC折叠后,点D恰好落在DC的延长线上的点E处.若
沿AC折叠后,点D恰好落在DC的延长线上的点E处.若 ,
, ,则
,则 的周长为( )
的周长为( )

 中,将
中,将 沿AC折叠后,点D恰好落在DC的延长线上的点E处.若
沿AC折叠后,点D恰好落在DC的延长线上的点E处.若 ,
, ,则
,则 的周长为( )
的周长为( )
| A.12 | B.15 | C.18 | D.21 |
6.从1、2、3、4四个数中随机选取两个不同的数,分别记为 、
、 ,则关于
,则关于 的一元二次方程
的一元二次方程 有实数解的概率为( )
有实数解的概率为( )
 、
、 ,则关于
,则关于 的一元二次方程
的一元二次方程 有实数解的概率为( )
有实数解的概率为( )A. | B. | C. | D. |
7.如图,在矩形 中,
中, ,
, ,过对角线交点
,过对角线交点 作
作 交
交 于点
于点 ,交
,交 于点
于点 ,则
,则 的长是( )
的长是( )

 中,
中, ,
, ,过对角线交点
,过对角线交点 作
作 交
交 于点
于点 ,交
,交 于点
于点 ,则
,则 的长是( )
的长是( )
| A.1 | B. | C.2 | D. |
8.如图,抛物线 为常数)交
为常数)交 轴于点
轴于点 ,与
,与 轴的一个交点在
轴的一个交点在 和
和 之间,顶点为
之间,顶点为 ,下列结论:
,下列结论:
①抛物线 与直线
与直线 有且只有一个交点;
有且只有一个交点;
②若点 在该抛物线上,则
在该抛物线上,则 ;
;
③将抛物线向左平移 个单位,再向下平移
个单位,再向下平移 个单位,所得抛物线的表达式为
个单位,所得抛物线的表达式为 .
.
其中正确的个数为( )

 为常数)交
为常数)交 轴于点
轴于点 ,与
,与 轴的一个交点在
轴的一个交点在 和
和 之间,顶点为
之间,顶点为 ,下列结论:
,下列结论:①抛物线
 与直线
与直线 有且只有一个交点;
有且只有一个交点;②若点
 在该抛物线上,则
在该抛物线上,则 ;
;③将抛物线向左平移
 个单位,再向下平移
个单位,再向下平移 个单位,所得抛物线的表达式为
个单位,所得抛物线的表达式为 .
.其中正确的个数为( )

A. 个 个 | B.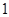 个 个 | C. 个 个 | D. 个 个 |
9.分解因式 ______.
______.
 ______.
______.10.如图,直线 ,将一块含
,将一块含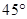 角的直角三角板
角的直角三角板 按如图方式放置,其中斜边
按如图方式放置,其中斜边 与直线
与直线 相交于点
相交于点 ,若
,若 ,则
,则 的度数为________.
的度数为________.
 ,将一块含
,将一块含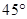 角的直角三角板
角的直角三角板 按如图方式放置,其中斜边
按如图方式放置,其中斜边 与直线
与直线 相交于点
相交于点 ,若
,若 ,则
,则 的度数为________.
的度数为________.
11.若 ,则
,则 的值为
的值为_______ .
 ,则
,则 的值为
的值为12.如图,点A,B,C在⊙O上,BC=6,∠BAC=60°,则⊙O的半径为______ .


13.如图,平面直角坐标系中,四边形 为菱形,点
为菱形,点 在
在 轴正半轴上,点
轴正半轴上,点 的坐标为
的坐标为 ,对角线
,对角线 相交于点
相交于点 ,则点
,则点 的坐标为______.
的坐标为______.
 为菱形,点
为菱形,点 在
在 轴正半轴上,点
轴正半轴上,点 的坐标为
的坐标为 ,对角线
,对角线 相交于点
相交于点 ,则点
,则点 的坐标为______.
的坐标为______.
14.如图,在直线 上方有一个正方形
上方有一个正方形 ,
, ,以点
,以点 为圆心,
为圆心, 为半径作弧,与
为半径作弧,与 交于点
交于点 ,分别以点
,分别以点 为圆心,
为圆心, 长为半径作弧,两弧交于点
长为半径作弧,两弧交于点 ,连结
,连结 ,则
,则 的度数为______.
的度数为______.
 上方有一个正方形
上方有一个正方形 ,
, ,以点
,以点 为圆心,
为圆心, 为半径作弧,与
为半径作弧,与 交于点
交于点 ,分别以点
,分别以点 为圆心,
为圆心, 长为半径作弧,两弧交于点
长为半径作弧,两弧交于点 ,连结
,连结 ,则
,则 的度数为______.
的度数为______.
15.计算: .
.
 .
.16.先化简,再求值: ;其中
;其中 .
.
 ;其中
;其中 .
.17.如图,四边形 中,点
中,点 在边
在边 上,
上, ,求证:
,求证: .
.

 中,点
中,点 在边
在边 上,
上, ,求证:
,求证: .
.
18.如图,某数学活动小组为测量学校旗杆 的高度,从旗杆正前方
的高度,从旗杆正前方 的
的 处出发,沿斜面坡度
处出发,沿斜面坡度 的斜坡
的斜坡 前进
前进 到达
到达 处,在
处,在 处垂直地面放置测量仪
处垂直地面放置测量仪 ,测得旗杆顶部
,测得旗杆顶部 的仰角为
的仰角为 ,测量仪
,测量仪 的高为
的高为 ,求旗杆
,求旗杆 的高度.
的高度.
 的高度,从旗杆正前方
的高度,从旗杆正前方 的
的 处出发,沿斜面坡度
处出发,沿斜面坡度 的斜坡
的斜坡 前进
前进 到达
到达 处,在
处,在 处垂直地面放置测量仪
处垂直地面放置测量仪 ,测得旗杆顶部
,测得旗杆顶部 的仰角为
的仰角为 ,测量仪
,测量仪 的高为
的高为 ,求旗杆
,求旗杆 的高度.
的高度.
19.某生态示范园计划种植一种水果,原计划总产量 万千克,为了满足市场需求,现决定改良水果品种,改良后平均每亩产量是原来的
万千克,为了满足市场需求,现决定改良水果品种,改良后平均每亩产量是原来的 倍,总产量比计划增加
倍,总产量比计划增加 万千克,种植面积可减少
万千克,种植面积可减少 亩,求改良后的水果平均每亩产量是多少万千克?
亩,求改良后的水果平均每亩产量是多少万千克?
 万千克,为了满足市场需求,现决定改良水果品种,改良后平均每亩产量是原来的
万千克,为了满足市场需求,现决定改良水果品种,改良后平均每亩产量是原来的 倍,总产量比计划增加
倍,总产量比计划增加 万千克,种植面积可减少
万千克,种植面积可减少 亩,求改良后的水果平均每亩产量是多少万千克?
亩,求改良后的水果平均每亩产量是多少万千克?20.如图,点 为反比例函数
为反比例函数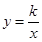 的图象上一点,在
的图象上一点,在 轴正半轴上有一点
轴正半轴上有一点 ,连接
,连接 ,且
,且 .
.

(1)求反比例函数的表达式;
(2)过点 作
作 轴交反比例函数
轴交反比例函数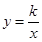 的图象于点
的图象于点 ,连接
,连接 ,求四边形
,求四边形 的面积.
的面积.
 为反比例函数
为反比例函数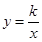 的图象上一点,在
的图象上一点,在 轴正半轴上有一点
轴正半轴上有一点 ,连接
,连接 ,且
,且 .
.
(1)求反比例函数的表达式;
(2)过点
 作
作 轴交反比例函数
轴交反比例函数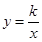 的图象于点
的图象于点 ,连接
,连接 ,求四边形
,求四边形 的面积.
的面积.21.某校为了解初中学生每天在校体育活动的时间(单位: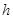 ),随机调查了该校的部.分学生,根据调查结果绘制出如下统计图:
),随机调查了该校的部.分学生,根据调查结果绘制出如下统计图:

(1)求调查的学生是多少人? .
(2)求调查的学生每天在校体育活动时间的平均数、众数;
(3)若该校有 名初中学生,估计该校每天在校体育活动时间大于
名初中学生,估计该校每天在校体育活动时间大于 的学生人数.
的学生人数.
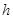 ),随机调查了该校的部.分学生,根据调查结果绘制出如下统计图:
),随机调查了该校的部.分学生,根据调查结果绘制出如下统计图:
(1)求调查的学生是多少人? .
(2)求调查的学生每天在校体育活动时间的平均数、众数;
(3)若该校有
 名初中学生,估计该校每天在校体育活动时间大于
名初中学生,估计该校每天在校体育活动时间大于 的学生人数.
的学生人数.22.如图, 是
是 的外接圆,
的外接圆, 的平分线交
的平分线交 于点
于点 ,交
,交 于点
于点 ,过
,过 作直线
作直线 ,连接
,连接 .
.

(1)求证: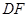 是
是 的切线;
的切线;
(2)若 ,求
,求 的长.
的长.
 是
是 的外接圆,
的外接圆, 的平分线交
的平分线交 于点
于点 ,交
,交 于点
于点 ,过
,过 作直线
作直线 ,连接
,连接 .
.
(1)求证:
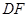 是
是 的切线;
的切线;(2)若
 ,求
,求 的长.
的长.23.在 中,
中, 是
是 上一点,连接
上一点,连接 .
.
(1)如图(1),若 是
是 延长线一点,
延长线一点, 与
与 垂直,求证:
垂直,求证: ;
;

(2)如图,若 是
是 的中点,过点
的中点,过点 作
作 于
于 ,连接
,连接 并延长交
并延长交 于点
于点 ,过点
,过点 作
作 ,交
,交 的延长线于点
的延长线于点 ,求
,求 .
.

 中,
中, 是
是 上一点,连接
上一点,连接 .
.(1)如图(1),若
 是
是 延长线一点,
延长线一点, 与
与 垂直,求证:
垂直,求证: ;
;
(2)如图,若
 是
是 的中点,过点
的中点,过点 作
作 于
于 ,连接
,连接 并延长交
并延长交 于点
于点 ,过点
,过点 作
作 ,交
,交 的延长线于点
的延长线于点 ,求
,求 .
.
24.如图,抛物线 经过点
经过点 ,交
,交 轴于点
轴于点 .
.

(1)求抛物线的函数表达式;
(2)点 为
为 轴右侧抛物线上一点,是否存在点
轴右侧抛物线上一点,是否存在点 使
使 ?若存在,求出点
?若存在,求出点 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
(3)将直线 绕点
绕点 顺时针旋转
顺时针旋转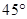 ,与直线
,与直线 相交于点
相交于点 ,求直线
,求直线 的函数表达式.
的函数表达式.
 经过点
经过点 ,交
,交 轴于点
轴于点 .
.
(1)求抛物线的函数表达式;
(2)点
 为
为 轴右侧抛物线上一点,是否存在点
轴右侧抛物线上一点,是否存在点 使
使 ?若存在,求出点
?若存在,求出点 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.(3)将直线
 绕点
绕点 顺时针旋转
顺时针旋转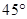 ,与直线
,与直线 相交于点
相交于点 ,求直线
,求直线 的函数表达式.
的函数表达式. 搜索
搜索
 难度系数:0.65
难度系数:0.65  答案解析
答案解析
 有奖纠错
有奖纠错
