搜索
全一卷
难度系数：0.65 
答案解析
有奖纠错
1．在
，﹣1，0，
，这四个数中，最小的实数是( )
，﹣1，0，
，这四个数中，最小的实数是( )| A． | B．﹣1 | C．0 | D． |
2．如图所示几何体的俯视图是( )
A． | B． | C． | D． |
3．五名女生的体重（单位：kg）分别为：37、40、38、42、42，这组数据的众数和中位数分别是（ ）
| A．2、40 | B．42、38 | C．40、42 | D．42、40 |
4．如图，数轴上有M、N、P、Q四个点，其中点P所表示的数为a，则数-3a所对应的点可能是( )
| A．M | B．N | C．P | D．Q |
5．随着“互联网+”时代的到来，一种新型的打车方式受到大众欢迎．打车总费用y(单位：元)与行驶里程x(单位：千米)的函数关系如图所示．如果小明某次打车行驶里程为22千米，则他的打车费用为( )
| A．33元 | B．36元 | C．40元 | D．42元 |
6．如图，平面上有两个全等的正八边形ABCDEFGH、A′B′C′D′E′F′G′H′，若点B与点B′重合，点H与点H′重合，则∠ABA′的度数为（ ）
| A．15° | B．30° | C．45° | D．60° |
7．点A(2，1)经过某种图形变换后得到点B(﹣1，2)，这种图形变化可以是( )
| A．关于x轴对称 | B．关于y轴对称 |
| C．绕原点逆时针旋转90° | D．绕原点顺时针旋转90° |
8．如图，在矩形ABCD中，点E在CD上，且DE：CE＝1：3，以点A为圆心，AE为半径画弧，交BC于点F，若F是BC中点，则AD：AB的值是( )
| A．6：5 | B．5：4 | C．6： | D．：2 |
9．如图，P是抛物线y＝x2﹣x﹣4在第四象限的一点，过点P分别向x轴和y轴作垂线，垂足分别为A、B，则四边形OAPB周长的最大值为( )
| A．10 | B．8 | C．7.5 | D．5 |
10．如图，Rt△ABC中，∠ACB＝90°，AC＝4，BC＝6，点D在BC上，延长BC至点E，使CE=
BD，F是AD的中点，连接EF，则EF的长是( )
BD，F是AD的中点，连接EF，则EF的长是( )
A． | B． | C．3 | D．4 |
11．分解因式2x2－8的结果是_________；
12．如果一个正多边形的内角和等于720°，那么该正多边形的一个外角等于_____ 度．
13．为了奖励校运会优秀运动员，学校决定用1200元购买篮球和排球两种奖品若干个．其中篮球每个120元，排球每个90元，在购买资金恰好用尽的情况下，购买方案有_____ ．
14．如图，在平面直角坐标系中，矩形ABCD的BC边落在y轴上，其它部分均在第二象限，双曲线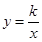
过点A，延长对角线CA交x轴于点E，以从AD、AE为边作平行四边形AEFD，若平行四边形AEFD的面积为2，则k的值为_____ ．
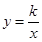过点A，延长对角线CA交x轴于点E，以从AD、AE为边作平行四边形AEFD，若平行四边形AEFD的面积为2，则k的值为
15．如图，在Rt△ABC中，∠ACB＝90°，∠BAC＝30°，BC＝4，D是AB上一个动点，将点D绕点C顺时针旋转60°，得到点E，连接A
| A．若AE＝，则BD＝_____． |
16．(1)计算：(﹣1)8+24×(﹣2)﹣3﹣
(2)化简：
(2)化简：
17．如图，在▱ABCD中，E，F分别为BC，AB中点，连接FC，AE，且AE与FC交于点G，AE的延长线与DC的延长线交于点N．
（1）求证：△ABE≌△NCE；
（2）若AB=3n，FB=
GE，试用含n的式子表示线段AN的长．
（1）求证：△ABE≌△NCE；
（2）若AB=3n，FB=
GE，试用含n的式子表示线段AN的长．
18．为了了解同学们对垃圾分类知识的了解程度，增强同学们的环保意识某校数学兴趣小组设计了“垃圾分类知识及投放情况”问卷，并在本校随机抽取若干名同学进行了问卷测试，根据测试成绩分布情况，将测试成绩分成A、B、C、D四组，绘制了如下统计图表
问卷测试成绩分组表
（1）本次抽样调查的样本总量是 ；
（2）样本中，测试成绩在B组的频数是 ，D组的频率是 ；
（3）样本中，这次测试成绩的中位数落在 组；
（4）如果该校共有880名学生，请估计成绩在90＜x≤100的学生约有 人．
问卷测试成绩分组表
| 组别 | 分数/分 |
| A | 60＜x≤70 |
| B | 70＜x≤80 |
| C | 80＜x≤90 |
| D | 90＜x≤100 |
（1）本次抽样调查的样本总量是 ；
（2）样本中，测试成绩在B组的频数是 ，D组的频率是 ；
（3）样本中，这次测试成绩的中位数落在 组；
（4）如果该校共有880名学生，请估计成绩在90＜x≤100的学生约有 人．
19．如图，平面直角坐标系xOy中，平行四边形OABC的B，C两点在第一象限，点A在x轴正半轴上．
(1)请用直尺(不带刻度)和圆规作一个圆，使其圆心D在对角线OB上，DO为半径，该圆和BC所在直线相切于点E；(作图不必写作法，但要保留作图痕迹．)
(2)在(1)中，若点B坐标为(4，3)，求点E的坐标．
(1)请用直尺(不带刻度)和圆规作一个圆，使其圆心D在对角线OB上，DO为半径，该圆和BC所在直线相切于点E；(作图不必写作法，但要保留作图痕迹．)
(2)在(1)中，若点B坐标为(4，3)，求点E的坐标．
20．已知，如图，A点坐标是(1，3)，B点坐标是(5，1)，C点坐标是(1，1)
(1)求△ABC的面积是____；
(2)求直线AB的表达式；
(3)一次函数y＝kx+2与线段AB有公共点，求k的取值范围；
(4)y轴上有一点P且△ABP与△ABC面积相等，则P点坐标是_____．
(1)求△ABC的面积是____；
(2)求直线AB的表达式；
(3)一次函数y＝kx+2与线段AB有公共点，求k的取值范围；
(4)y轴上有一点P且△ABP与△ABC面积相等，则P点坐标是_____．
21．如图，在Rt△ABC中，∠ACB＝90°，E是BC的中点，以AC为直径的⊙O与AB边交于点D，连接DE．
(1)求证：DE是⊙O的切线；
(2)若CD＝6cm，DE＝5cm，求⊙O直径的长．
(1)求证：DE是⊙O的切线；
(2)若CD＝6cm，DE＝5cm，求⊙O直径的长．
22．甲、乙两人在笔直的道路AB上相向而行，甲骑自行车从A地到B地，乙驾车从B地到A地，假设他们分别以不同的速度匀速行驶，甲先出发6分钟后，乙才出发，乙的速度为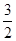
千米/分，在整个过程中，甲、乙两人之间的距离y(千米)与甲出发的时间x(分)之间的部分函数图象如图．
(1)A、B两地相距____千米，甲的速度为____千米/分；
(2)求线段EF所表示的y与x之间的函数表达式；
(3)当乙到达终点A时，甲还需多少分钟到达终点B？
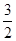千米/分，在整个过程中，甲、乙两人之间的距离y(千米)与甲出发的时间x(分)之间的部分函数图象如图．(1)A、B两地相距____千米，甲的速度为____千米/分；
(2)求线段EF所表示的y与x之间的函数表达式；
(3)当乙到达终点A时，甲还需多少分钟到达终点B？
23．如图，A(0，2)，B(6，2)，C(0，c)(c＞0)，以A为圆心AB长为半径的
交y轴正半轴于点D，与BC有交点时，交点为E，P为上一点．
(1)若c＝6
+2，
①BC＝_____，
的长为_____；
②当CP＝6时，判断CP与⊙A的位置关系，并加以证明；
(2)若c＝10，求点P与BC距离的最大值；
(3)分别直接写出当c＝1，c＝6，c＝9，c＝11时，点P与BC的最大距离(结果无需化简)
交y轴正半轴于点D，与BC有交点时，交点为E，P为上一点．(1)若c＝6
+2，①BC＝_____，
的长为_____；②当CP＝6
时，判断CP与⊙A的位置关系，并加以证明；(2)若c＝10，求点P与BC距离的最大值；
(3)分别直接写出当c＝1，c＝6，c＝9，c＝11时，点P与BC的最大距离(结果无需化简)
