搜索
全一卷
难度系数：0.94 
答案解析
有奖纠错
1．计算4＋(－8)÷(－4)－(－1) 的结果是（ ）
| A．2 | B．3 | C．7 | D． |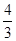
2．铺设木地板时，每两块地板之间的缝隙不低于0.5mm且不超过0.8mm，缝隙的宽度可以是（ ）
| A．0.3 mm | B．0.4 mm | C．0.6 mm | D．0.9 mm |
3．若△ABC∽△DEF，相似比为1∶2，则△ABC与△DEF的面积的比为（ ）
A． ：1 | B．1∶ | C．4∶1 | D．1∶4 |
4．今年4月30日，江苏省约有四百万辆车涌入高速公路，用科学记数法表示“四百万”是（ ）
| A．4×104 | B．4×105 | C．4×106 | D．4×107 |
5．75年中国登山队成功登顶珠穆朗玛峰，下图是当年5月18~28日珠峰海拔8km、9km处风速变化的真实记录，从图中可得到的正确结论是（ ）
①同一天中，海拔越高，风速越大；
②从风速变化考虑，27日适合登山；
③海拔8 km处的平均风速约为20 m/s．
①同一天中，海拔越高，风速越大；
②从风速变化考虑，27日适合登山；
③海拔8 km处的平均风速约为20 m/s．
| A．①② | B．①③ | C．②③ | D．①②③ |
6．如图，△ABC中，∠BAC＝45°，∠ABC＝60°，AB＝4，D是边BC上的一个动点，以AD为直径画⊙O分别交AB、AC于点E、F，则弦EF长度的最小值为（ ）
A． | B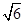． | C．2 | D．2 |
7．8的平方根是__________ ，8的立方根是__________ ．
8．若式子
在实数范围内有意义，则x的取值范围是___．
在实数范围内有意义，则x的取值范围是___．9．计算
的结果是___．
的结果是___．10．已知3＋
是关于x的方程x2－6x＋m＝0的一个根，则m＝_____．
是关于x的方程x2－6x＋m＝0的一个根，则m＝_____．11．若△ABC的三边长为3、4、5，则△ABC的外接圆半径R与内切圆半径r的差为___ ．
12．如图，四边形ABCD内接于⊙O，AC平分∠BAD．若∠BDC＝40°，则∠BCD的度数为___°．
13．点O、A、B、C在数轴上的位置如图所示，O为原点，BC＝3，OA＝OC，若B表示的数为x，则A表示的数为___．（用含x的代数式表示）
14．把一副三角板如图摆放，其中∠C＝∠E＝90°，∠A＝45°，∠F＝30°，则∠1＋∠2＝____ °．
15．若反比例函数y＝
的图像与一次函数y＝mx＋n的图像的交点的横坐标为1和－3，则关于x的方程＝mx－n的解是___．
的图像与一次函数y＝mx＋n的图像的交点的横坐标为1和－3，则关于x的方程＝mx－n的解是___．16．如图是一张直角三角形卡片，∠ACB＝90°，AC＝BC，点D、E分别在边AB、AC上，AD＝2 cm，DB＝4 cm，DE⊥AB．若将该卡片绕直线DE旋转一周，则形成的几何体的表面积为___cm2．
17．计算(2a－1)2＋2(2a－1)＋3．
18．（1）化简
；
（2）解方程＝0．
；（2）解方程
＝0．19．如图，△ABC中，D、E分别是边AB、AC的中点，点F是BC上一点，∠B＝∠DEF．
（1）求证：四边形BDEF是平行四边形；
（2）直接写出当△ABC满足什么条件时，四边形BDEF是菱形．
（1）求证：四边形BDEF是平行四边形；
（2）直接写出当△ABC满足什么条件时，四边形BDEF是菱形．
20．商店以7元/件的进价购入某种文具1 000件，按10元/件的售价销售了500件．现对剩下的这种文具降价销售，如果要保证总利润不低于2 000元，那么剩下的文具最低定价是多少元？
21．某篮球队员在篮球联赛中分别与甲队、乙队对阵各四场，下表是他的技术统计．
（1）他在对阵甲队和乙队的各四场比赛中，平均每场得分分别是多少？
（2）利用方差判断他在对阵哪个队时得分比较稳定；
（3）根据上表提供的信息，判断他在对阵哪个队时总体发挥较好，简要说明理由．
场次 | 对阵甲队 | 对阵乙队 | ||
得分（分） | 失误（次） | 得分（分） | 失误（次） | |
第一场 | 25 | 2 | 27 | 3 |
第二场 | 30 | 0 | 31 | 1 |
第三场 | 27 | 3 | 20 | 2 |
第四场 | 26 | 2 | 26 | 4 |
（1）他在对阵甲队和乙队的各四场比赛中，平均每场得分分别是多少？
（2）利用方差判断他在对阵哪个队时得分比较稳定；
（3）根据上表提供的信息，判断他在对阵哪个队时总体发挥较好，简要说明理由．
22．甲盒中有标号为1、2、4的牌子，乙盒中有标号为1、2、3、4的牌子，两个盒子均不透明，这些牌子除标号外无其他差别．小勇从甲盒中随机摸出一个牌子，标号为a，小婷从乙盒中随机摸出一个牌子，标号为b，若a＜b，则小勇获胜；若a≥b，则小婷获胜．
（1）求小勇获胜的概率；
（2）若小勇摸出的牌子标号为2，在不知道小婷标号的情况下，他获胜的概率是 ．
（1）求小勇获胜的概率；
（2）若小勇摸出的牌子标号为2，在不知道小婷标号的情况下，他获胜的概率是 ．
23．如图1，点A、B在直线MN上（A在B的左侧），点P是直线MN上方一点．若∠PAN＝x°，∠PBN＝y°，记< x，y >为P的双角坐标．例如，若△PAB是等边三角形，则点P的双角坐标为<60，120>．
（1）如图2，若AB＝22 cm，P＜26.6，58＞，求△PAB的面积；
（参考数据：tan26.6°≈0.50，tan58°≈1.60．）
（2）在图3中用直尺和圆规作出点P < x，y >，其中y＝2x且y＝x＋30．（保留作图痕迹）
（1）如图2，若AB＝22 cm，P＜26.6，58＞，求△PAB的面积；
（参考数据：tan26.6°≈0.50，tan58°≈1.60．）
（2）在图3中用直尺和圆规作出点P < x，y >，其中y＝2x且y＝x＋30．（保留作图痕迹）
24．如图，D是△ABC边BC上的点，连接AD，∠BAD＝∠CAD，BD＝CD．
用两种不同方法证明AB＝AC．
用两种不同方法证明AB＝AC．
25．已知二次函数y＝ax2－6ax＋5a（a为常数）的图像为抛物线C．
（1）求证：不论a为何值，抛物线C与x轴总有两个不同的公共点；
（2）设抛物线C交x轴于点A、B，交y轴于点D，若△ABD的面积为20，求a的值；
（3）设点E（2，4）、F（3，4），若抛物线C与线段EF只有一个公共点，结合函数图像，直接写出a的取值范围．
（1）求证：不论a为何值，抛物线C与x轴总有两个不同的公共点；
（2）设抛物线C交x轴于点A、B，交y轴于点D，若△ABD的面积为20，求a的值；
（3）设点E（2，4）、F（3，4），若抛物线C与线段EF只有一个公共点，结合函数图像，直接写出a的取值范围．
26．如图，矩形ABCD中，E是BC的中点，连接DE，P是DE上一点，∠BPC＝90°，延长CP交AD于点F．⊙O经过P、D、F，交CD于点G．
（1）求证：DF
DP；
（2）若
，
，求DG的长；
（3）连接BF，若BF是⊙O的切线，直接写出
的值．
（1）求证：DF
DP；（2）若
，
，求DG的长；（3）连接BF，若BF是⊙O的切线，直接写出
的值．27．如图1，汽车以速度V（m/s）匀速行驶，若一路绿灯通过路口A、B、C、D且10≤V≤25，则称V为绿灯速度．已知各路口红灯、绿灯均每隔30 s交替一次，其余因素忽略不计．
（图1）
I．从红绿灯设置到绿灯速度
设汽车在第0秒出发，行驶t s后路程为S m．图2表示在某种红绿灯设置下汽车行驶的情况．
（2）求出射线OC3所对应的V的值，判断此时V是否为绿灯速度，并说明理由；
（3）写出这种红绿灯设置下绿灯速度的取值范围，并在图2中画出对应的示意图
II．从绿灯速度到红绿灯设置
（4）当V＝20时，汽车经过的每个路口绿灯都恰好开始亮起．根据题意，在图3中画图表示各路口的红绿灯设置．
（图1）
I．从红绿灯设置到绿灯速度
设汽车在第0秒出发，行驶t s后路程为S m．图2表示在某种红绿灯设置下汽车行驶的情况．
（图2）
（1）路段BC的长度为______m，路口A绿灯亮起______s后路口D绿灯亮起；（2）求出射线OC3所对应的V的值，判断此时V是否为绿灯速度，并说明理由；
（3）写出这种红绿灯设置下绿灯速度的取值范围，并在图2中画出对应的示意图
II．从绿灯速度到红绿灯设置
（4）当V＝20时，汽车经过的每个路口绿灯都恰好开始亮起．根据题意，在图3中画图表示各路口的红绿灯设置．
（图3）
