全一卷
1.使式子 有意义的x的取值范围是( )
有意义的x的取值范围是( )
 有意义的x的取值范围是( )
有意义的x的取值范围是( )A. | B. | C. | D. |
2.下列计算正确的是( )
A. + + = = | B.3 -2 -2 =3 =3 | C.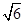 ÷2= ÷2= | D. =2 =2 |
3.一组数据4,6,5,5,10中,平均数是( )
| A.5 | B.6 | C.7 | D.8 |
4.下列各组数据中的三个数作为三角形的边长,其中能构成直角三角形的是( )
A. ,2, ,2, | B.2,3,4 | C.6,7, 8 | D.3,4,5 |
5.关于四边形对角线的性质,矩形具有而菱形不一定具有的是( )
| A.对角线互相平分 | B.对角线互相垂直 |
| C.对角线相等 | D.对角线平分一组对角 |
6.某蓄水池的横断面示意图如图所示,分深水区和浅水区,如果这个注满水的蓄水池以固定的流量把水全部放出,下面的图象能大致表示水的深度h和放水时间t之间的关系的是( )


A. | B. | C. | D. |
7.李老师为了了解学生在家的阅读情况,随机抽样调查了20名学生某一天的阅读时间,具体情况统计如下:
则关于这20名学生阅读时间所组成的一组数据中,下列说法正确的是( )
| 阅读时间(小时) | 1 | 1.5 | 2 | 2.5 | 3 |
| 学生人数(名) | 1 | 2 | 8 | 6 | 3 |
则关于这20名学生阅读时间所组成的一组数据中,下列说法正确的是( )
| A.中位数是2 | B.中位数是2.5 | C.众数是8 | D.众数是3 |
8.关于函数 ,下列结论正确的是( )
,下列结论正确的是( )
 ,下列结论正确的是( )
,下列结论正确的是( )A.图象必经过点 |
| B.图象经过第一、二、三象限 |
C.当 时, 时, |
D. 随 随 的增大而增大 的增大而增大 |
9.如图,正方形ABCD的边长为4,点E在对角线BD上,且∠DAE=67.5°,EF⊥AB,垂足为F,则EF的长为( )


| A.1 | B. | C.4-2 | D.3 -4 -4 |
10.如图,点C是线段AB上一点,分别以AC,BC为边在线段AB的同侧作等边△ACD和等边△BCE,连结DE,点F为DE的中点,连结CF.若AB=2a(a为常数,a>0),当点C在线段AB上运动时,线段CF的长度l的取值范围是( )


A. | B. | C. | D. |
11.已知正比例函数经过点P(a,3a)(其中a为常数,a≠0),则该正比例函数解析式为__________ .
12.直线y=-2x+2向上平移2个单位后的解析式为_____________.
13.甲、乙两人进行射击比赛,在相同条件下各射击10次.已知他们的平均成绩相同,方差分别是S甲2=2.6,S乙2=3,那么甲、乙两人成绩较为稳定的是_______.
14.小强和小明相约在某公共汽车站一起乘车回学校,小强从家出发步行先到车站,等小明到了后两人一起乘公共汽车回到学校,图中折线表示小强离开家的路程y(公里)和所用时间x(分)之间的函数关系,则公共汽车的平均速度是________公里/小时.

15.如图,在△ABC中,点D,点E分别是AB,AC的中点,点F是DE上一点,∠AFC=90°,BC=10cm,AC=6cm,则DF=________ cm.


16.如图,在平面直角坐标系中,直线AB的解析式为y=-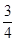 x+3.点C是AO上一点且OC=1,点D在线段BO上,分别连接BC,AD交于点E,若∠BED=45°,则OD的长是________.
x+3.点C是AO上一点且OC=1,点D在线段BO上,分别连接BC,AD交于点E,若∠BED=45°,则OD的长是________.
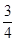 x+3.点C是AO上一点且OC=1,点D在线段BO上,分别连接BC,AD交于点E,若∠BED=45°,则OD的长是________.
x+3.点C是AO上一点且OC=1,点D在线段BO上,分别连接BC,AD交于点E,若∠BED=45°,则OD的长是________.
17.计算:(1)  (2)
(2) 
 (2)
(2) 
18.点O为△ABC内一动点,D,E,F,G分别为AB,AC,OB,OC中点.求证:四边形DEFG为平行四边形.

19.某同学在本学期的数学成绩如下表所示(成绩均取整数):
(1)计算该同学本学期的平时平均成绩;
(2)如果学期的总评成绩是根据如图所示的权重计算,那么本学期该同学的期末考试成绩x至少为多少分才能保证达到总评成绩90分的最低目标?
测验 类别 | 平时 | 期中 考试 | 期末 考试 | |||
测验1 | 测验2 | 测验3 | 课题 学习 | |||
成绩 | 89 | 77 | 94 | 88 | 87 | x |
(1)计算该同学本学期的平时平均成绩;
(2)如果学期的总评成绩是根据如图所示的权重计算,那么本学期该同学的期末考试成绩x至少为多少分才能保证达到总评成绩90分的最低目标?

20.如图,A(-4,1),B(1,1),C(-3,3)都在边长为1个单位的正方形网格的格点上.
(1)判断△ABC的形状,并说明理由;
(2)画出点C关于直线AB的对称点D,连CD,BD.直接写出△CDB的面积为 ;
(3)点P,Q分别为边AB,BC上的动点,仅用无刻度的直尺画出点P,Q的位置,使得CP+PQ最小;(保留连线痕迹)
(4)在(3)的条件下,直接写出CP+PQ的最小值为 .
(1)判断△ABC的形状,并说明理由;
(2)画出点C关于直线AB的对称点D,连CD,BD.直接写出△CDB的面积为 ;
(3)点P,Q分别为边AB,BC上的动点,仅用无刻度的直尺画出点P,Q的位置,使得CP+PQ最小;(保留连线痕迹)
(4)在(3)的条件下,直接写出CP+PQ的最小值为 .

21.如图,在矩形ABCD中,∠BAD 的平分线交BC于点E,AE=AD,作DF⊥AE于点F.
(1)求证:AB=AF;
(2)连BF并延长交DE于G.
①EG=DG;
②若EG=1,求矩形ABCD的面积.

(1)求证:AB=AF;
(2)连BF并延长交DE于G.
①EG=DG;
②若EG=1,求矩形ABCD的面积.

22.某公司装修需用A型板材240块、B型板材180块,A型板材规格是60cm×30cm,B型板材规格是40cm×30cm.现只能购得规格是150cm×30cm的标准板材.一张标准板材尽可能多地裁出A型、B型板材,共有下列三种裁法:(如图是裁法一的裁剪示意图)
设所购的标准板材全部裁完,其中按裁法一裁x张、按裁法二裁y张、按裁法三裁z张,且所裁出的A、B两种型号的板材刚好够用.
(1)上表中,m= _____,n= ____;
(2)分别求出y与x和z与x的函数关系式;
(3)若用Q表示所购标准板材的张数,求Q与x的函数关系式,并指出当x取何值时Q最小,此时按三种裁法各裁标准板材多少张?

| | 裁法一 | 裁法二 | 裁法三 |
| A型板材块数 | 1 | 2 | 0 |
| B型板材块数 | 2 | m | n |
(1)上表中,m= _____,n= ____;
(2)分别求出y与x和z与x的函数关系式;
(3)若用Q表示所购标准板材的张数,求Q与x的函数关系式,并指出当x取何值时Q最小,此时按三种裁法各裁标准板材多少张?

23.如图平行四边形ABCD,E,F分别是AD,BC上的点,且AE=CF,EF与AC交于点O.
(1)如图①.求证:OE=OF;
(2)如图②,将平行四边形ABCD(纸片沿直线EF折叠,点A落在A1处,点B落在点B1处,设FB交CD于点G.A1B分别交CD,DE于点H,P.请在折叠后的图形中找一条线段,使它与EP相等,并加以证明;
(3)如图③,若△ABO是等边三角形,AB=4,点F在BC边上,且BF=4.则 = (直接填结果).
= (直接填结果).
(1)如图①.求证:OE=OF;
(2)如图②,将平行四边形ABCD(纸片沿直线EF折叠,点A落在A1处,点B落在点B1处,设FB交CD于点G.A1B分别交CD,DE于点H,P.请在折叠后的图形中找一条线段,使它与EP相等,并加以证明;
(3)如图③,若△ABO是等边三角形,AB=4,点F在BC边上,且BF=4.则
 = (直接填结果).
= (直接填结果).
24.如图,在平面直角坐标系中,直线y=-4x与直线y=4相交于点A,点P(a,b)为直线y=4上一动点,作直线OP.
(1)当点P在运动过程中,若△AOP 的面积为8,求直线OP的解析式;
(2)若点P在运动过程中,若∠AOP=45°,求点P的坐标;
(3)在(2)的条件下,点M是直线OP上一动点,且位于x轴上方,连接MA.设点M的横坐标为m,记△MAO的面积为S,求S与m的函数关系式.
(1)当点P在运动过程中,若△AOP 的面积为8,求直线OP的解析式;
(2)若点P在运动过程中,若∠AOP=45°,求点P的坐标;
(3)在(2)的条件下,点M是直线OP上一动点,且位于x轴上方,连接MA.设点M的横坐标为m,记△MAO的面积为S,求S与m的函数关系式.

 搜索
搜索
 难度系数:0.94
难度系数:0.94  答案解析
答案解析
 有奖纠错
有奖纠错
