全一卷
1.抛物线y=﹣(x+2)2﹣3的顶点坐标是( )
| A.(2,﹣3) | B.(﹣2,3) | C.(2,3) | D.(﹣2,﹣3) |
2.如图,点D、E分别在△ABC的边AB、AC上,下列条件中能够判定DE∥BC的是( )
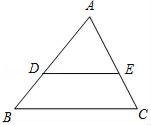

A. | B. | C. | D. |
3.在Rt△ABC中,∠C=90°,如果cosB= ,BC=a,那么AC的长是( )
,BC=a,那么AC的长是( )
 ,BC=a,那么AC的长是( )
,BC=a,那么AC的长是( )A. | B.3a | C. | D. |
4.如果|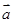 |=2,
|=2,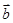 =-
=-
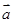 ,那么下列说法正确的是( )
,那么下列说法正确的是( )
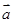 |=2,
|=2,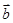 =-
=-
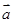 ,那么下列说法正确的是( )
,那么下列说法正确的是( )A.|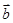 |=2| |=2|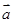 | | | B.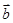 是与 是与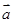 方向相同的单位向量 方向相同的单位向量 |
C.2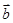 - -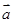 = = | D.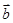 ∥ ∥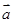 |
5.在直角坐标平面内,点O是坐标原点,点A的坐标是(3,2),点B的坐标是(3,﹣4).如果以点O为圆心,r为半径的圆O与直线AB相交,且点A、B中有一点在圆O内,另一点在圆O外,那么r的值可以取( )
| A.5 | B.4 | C.3 | D.2 |
6.在△ABC中,点D在边BC上,联结AD,下列说法错误的是( )
| A.如果∠BAC=90°,AB2=BD•BC,那么AD⊥BC |
| B.如果AD⊥BC,AD2=BD•CD,那么∠BAC=90° |
| C.如果AD⊥BC,AB2=BD•BC,那么∠BAC=90° |
| D.如果∠BAC=90°,AD2=BD•CD,那么AD⊥BC |
7.若线段a、b、c、d满足 ,则
,则 的值等于_____.
的值等于_____.
 ,则
,则 的值等于_____.
的值等于_____.8.如果抛物线y=(3﹣m)x2﹣3有最高点,那么m的取值范围是_____.
9.如果两个相似三角形的周长的比等于1:4,那么它们的面积的比等于_____ .
10.边长为6的正六边形的边心距为_____ .
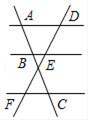
11.如图,已知AD∥BE∥CF,若AB=3,AC=7,EF=6,则DE的长为_____ .

12.若点A(﹣1,7)、B(5,7)、C(﹣2,﹣3)、D(k,﹣3)在同一条抛物线上,则k的值等于_____ .
13.如图,在一条东西方向笔直的沿湖道路l上有A、B两个游船码头,观光岛屿C在码头A的北偏东60°方向、在码头B的北偏西45°方向,AC=4千米.那么码头A、B之间的距离等于_____ 千米.(结果保留根号)


14.在矩形ABCD中,AB=2,AD=4,若圆A的半径长为5,圆C的半径长为R,且圆A与圆C内切,则R的值等于_____.
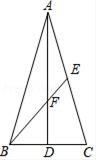
15.如图,在等腰△ABC中,AB=AC,AD、BE分别是边BC、AC上的中线,AD与BE交于点F,若BE=6,FD=3,则△ABC的面积等于_____.

16.已知点P在△ABC内,连接PA、PB、PC,在△PAB、△PBC和△PAC中,如果存在一个三角形与△ABC相似,那么就称点P为△ABC的自相似点.如图,在Rt△ABC中,∠ACB=90°,AC=12,BC=5,如果点P为Rt△ABC的自相似点,那么∠ACP的余切值等于_____.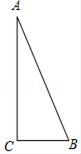

17.如图,点P在平行四边形ABCD的边BC上,将△ABP沿直线AP翻折,点B恰好落在边AD的垂直平分线上,如果AB=5,AD=8,tanB= ,那么BP的长为_____.
,那么BP的长为_____.
 ,那么BP的长为_____.
,那么BP的长为_____.
18.计算: .
.
 .
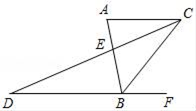
.19.如图,AB与CD相交于点E,AC∥BD,点F在DB的延长线上,联结BC,若BC平分∠ABF,AE=2,BE=3.
(1)求BD的长;
(2)设 =
=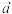 ,
,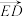 =
= ,用含
,用含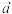 、
、 的式子表示
的式子表示 .
.
(1)求BD的长;
(2)设
 =
=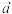 ,
,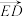 =
= ,用含
,用含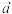 、
、 的式子表示
的式子表示 .
.
20.如图,AB是圆O的一条弦,点O在线段AC上,AC=AB,OC=3,sinA=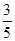 .求:(1)圆O的半径长;(2)BC的长.
.求:(1)圆O的半径长;(2)BC的长.
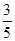 .求:(1)圆O的半径长;(2)BC的长.
.求:(1)圆O的半径长;(2)BC的长.
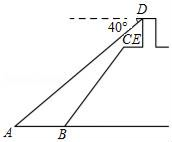
21.如图,小明站在江边某瞭望台DE的顶端D处,测得江面上的渔船A的俯角为40°.若瞭望台DE垂直于江面,它的高度为3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i=1:0.75,坡长BC=10米.
(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,cot40°≈1.19)
(1)求瞭望台DE的顶端D到江面AB的距离;
(2)求渔船A到迎水坡BC的底端B的距离.(结果保留一位小数)
(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,cot40°≈1.19)
(1)求瞭望台DE的顶端D到江面AB的距离;
(2)求渔船A到迎水坡BC的底端B的距离.(结果保留一位小数)

22.如图,点D、E分别在△ABC的边AC、AB上,延长DE、CB交于点F,且AE•AB=AD•AC.
(1)求证:∠FEB=∠C;
(2)连接AF,若 ,求证:EF•AB=AC•FB.
,求证:EF•AB=AC•FB.

(1)求证:∠FEB=∠C;
(2)连接AF,若
 ,求证:EF•AB=AC•FB.
,求证:EF•AB=AC•FB.
23.如图,在直角坐标平面内,抛物线经过原点O、点B(1,3),又与x轴正半轴相交于点A,∠BAO=45°,点P是线段AB上的一点,过点P作PM∥OB,与抛物线交于点M,且点M在第一象限内.
(1)求抛物线的表达式;
(2)若∠BMP=∠AOB,求点P的坐标;
(3)过点M作MC⊥x轴,分别交直线AB、x轴于点N、C,若△ANC的面积等于△PMN的面积的2倍,求 的值.
的值.
(1)求抛物线的表达式;
(2)若∠BMP=∠AOB,求点P的坐标;
(3)过点M作MC⊥x轴,分别交直线AB、x轴于点N、C,若△ANC的面积等于△PMN的面积的2倍,求
 的值.
的值.
24.已知锐角∠MBN的余弦值为 ,点C在射线BN上,BC=25,点A在∠MBN的内部,且∠BAC=90°,∠BCA=∠MBN.过点A的直线DE分别交射线BM、射线BN于点D、
,点C在射线BN上,BC=25,点A在∠MBN的内部,且∠BAC=90°,∠BCA=∠MBN.过点A的直线DE分别交射线BM、射线BN于点D、
(1)如图1,当AF⊥BN时,求EF的长;
(2)如图2,当点E在线段BC上时,设BF=x,BD=y,求y关于x的函数解析式并写出函数定义域;
(3)联结DF,当△ADF与△ACE相似时,请直接写出BD的长.
 ,点C在射线BN上,BC=25,点A在∠MBN的内部,且∠BAC=90°,∠BCA=∠MBN.过点A的直线DE分别交射线BM、射线BN于点D、
,点C在射线BN上,BC=25,点A在∠MBN的内部,且∠BAC=90°,∠BCA=∠MBN.过点A的直线DE分别交射线BM、射线BN于点D、| A.点F在线段BE上(点F不与点B重合),且∠EAF=∠MBN. |
(2)如图2,当点E在线段BC上时,设BF=x,BD=y,求y关于x的函数解析式并写出函数定义域;
(3)联结DF,当△ADF与△ACE相似时,请直接写出BD的长.

 搜索
搜索
 难度系数:0.85
难度系数:0.85  答案解析
答案解析
 有奖纠错
有奖纠错
