搜索
全一卷
难度系数：0.94 
答案解析
有奖纠错
1．在﹣1，﹣2，0，1四个数中最小的数是（ ）
| A．-1 | B．-2 | C．0 | D．1 |
2．计算（2a）3的结果是（）
| A．6a | B．8a | C．2a3 | D．8a3 |
3．不等式组
的解集是
的解集是A． | B． | C． | D． |
4．若反比例函数
的图象经过点（5，﹣1）．则实数k的值是
的图象经过点（5，﹣1）．则实数k的值是A． | B． | C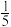． | D．5 |
5．若扇形的半径为6，圆心角为120°，则此扇形的弧长是（ ）
A． | B． | C． | D． |
6．如图,数轴上A,B两点表示的数分别为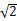
和5.1,则A,B两点之间表示整数的点共有 ( )
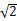和5.1,则A,B两点之间表示整数的点共有 ( )
| A．6个 | B．5个 | C．4个 | D．3个 |
7．若等腰三角形有两条边的长度为3和1，则此等腰三角形的周长为
| A．5 | B．7 | C．5或7 | D．6 |
8．如图，点A、B、C是⊙O上的三点，若∠OBC=50°，则∠A的度数是（ ）
| A．40° | B．50° | C．80° | D．100° |
9．sin30°的值为_____ ．
10．方程
的解集是_____ ．
的解集是11．点A（﹣3，0）关于y轴的对称点的坐标是__ ．
12．一组数据3，9，4，9，5的众数是_____ ．
13．若n边形的每一个外角都等于60°，则n=_____ ．
14．如图，三角板的直角顶点在直线l上，看∠1=40°，则∠2的度数是 ．
15．已知△ABC中，D、E分别是AB、AC边上的中点，且DE＝3cm，则BC＝___________ cm．
16．二次函数y=x2+1的图象的顶点坐标是_____ ．
17．若菱形的两条对角线分别为2和3，则此菱形的面积是_____ ．
18．观察一列单项式：1x，3x2，5x2，7x，9x2，11x2，…，则第2013个单项式是 ．
19．（1）计算：
（2）计算：
．
（2）计算：
．20．解不等式：
，并把解集在数轴上表示出来．
，并把解集在数轴上表示出来．
21．如图，在边长为1个单位长度的小正方形组成的两格中，点A、B、C都是格点．
（1）将△ABC向左平移6个单位长度得到得到△A1B1C1；
（2）将△ABC绕点O按逆时针方向旋转180°得到△A2B2C2，请画出△A2B2C2．
（1）将△ABC向左平移6个单位长度得到得到△A1B1C1；
（2）将△ABC绕点O按逆时针方向旋转180°得到△A2B2C2，请画出△A2B2C2．
22．如图，在平行四边形ABCD中，过AC中点O作直线，分别交AD、BC于点E、F．
求证：△AOE≌△COF．
求证：△AOE≌△COF．
23．如图，某中学为合理安排体育活动，在全校喜欢乒乓球、排球、羽毛球、足球、篮球五种球类运动的1000名学生中，随机抽取了若干名学生进行调查，了解学生最喜欢的一种球类运动，每人只能在这五种球类运动中选择一种．调查结果统计如下：
解答下列问题：
(1)本次调查中的样本容量是 ；
(2)
，
；
(3)试估计上述1000名学生中最喜欢羽毛球运动的人数．
| 球类名称 | 乒乓球 | 排球 | 羽毛球 | 足球 | 篮球 |
| 人数 | a | 12 | 36 | 18 | b |
(1)本次调查中的样本容量是 ；
(2)
， ；(3)试估计上述1000名学生中最喜欢羽毛球运动的人数．
24．一个不透明的袋子中装有大小、质地完全相同的3只球，球上分别标有2，3，5三个数字．
（1）从这个袋子中任意摸一只球，所标数字是奇数的概率是 ；
（2）从这个袋子中任意摸一只球，记下所标数字，不放回，再从从这个袋子中任意摸一只球，记下所标数字．将第一次记下的数字作为十位数字，第二次记下的数字作为个位数字，组成一个两位数．求所组成的两位数是5的倍数的概率．（请用“画树状图”或“列表”的方法写出过程）
（1）从这个袋子中任意摸一只球，所标数字是奇数的概率是 ；
（2）从这个袋子中任意摸一只球，记下所标数字，不放回，再从从这个袋子中任意摸一只球，记下所标数字．将第一次记下的数字作为十位数字，第二次记下的数字作为个位数字，组成一个两位数．求所组成的两位数是5的倍数的概率．（请用“画树状图”或“列表”的方法写出过程）
25．小丽为校合唱队购买某种服装时，商店经理给出了如下优惠条件：如果一次性购买不超过10件，单价为80元；如果一次性购买多于10件，那么每增加1件，购买的所有服装的单价降低2元，但单价不得低于50元．按此优惠条件，小丽一次性购买这种服装付了1200元．请问她购买了多少件这种服装？
26．如图，AB是⊙O的直径，C是⊙0上的一点，直线MN经过点C，过点A作直线MN的垂线，垂足为点D，且∠BAC=∠DAC
（1）猜想直线MN与⊙O的位置关系，并说明理由；
（2）若CD=6，cos∠ACD=
，求⊙O的半径．
（1）猜想直线MN与⊙O的位置关系，并说明理由；
（2）若CD=6，cos∠ACD=
，求⊙O的半径．27．甲、乙两地之间有一条笔直的公路L，小明从甲地出发沿公路ι步行前往乙地，同时小亮从乙地出发沿公路L骑自行车前往甲地，小亮到达甲地停留一段时间，原路原速返回，追上小明后两人一起步行到乙地．设小明与甲地的距离为y1米，小亮与甲地的距离为y2米，小明与小亮之间的距离为s米，小明行走的时间为x分钟．y1、y2与x之间的函数图象如图1，s与x之间的函数图象（部分）如图2．
（1）求小亮从乙地到甲地过程中y1（米）与x（分钟）之间的函数关系式；
（2）求小亮从甲地返回到与小明相遇的过程中s（米）与x（分钟）之间的函数关系式；
（3）在图2中，补全整个过程中s（米）与x（分钟）之间的函数图象，并确定a的值．
（1）求小亮从乙地到甲地过程中y1（米）与x（分钟）之间的函数关系式；
（2）求小亮从甲地返回到与小明相遇的过程中s（米）与x（分钟）之间的函数关系式；
（3）在图2中，补全整个过程中s（米）与x（分钟）之间的函数图象，并确定a的值．
28．如图，在△ABC中，∠C=90°，BC=3，AB=5．点P从点B出发，以每秒1个单位长度沿B→C→A→B的方向运动；点Q从点C出发，以每秒2个单位沿C→A→B方向的运动，到达点B后立即原速返回，若P、Q两点同时运动，相遇后同时停止，设运动时间为t秒．
（1）当t= 时，点P与点Q相遇；
（2）在点P从点B到点C的运动过程中，当ι为何值时，△PCQ为等腰三角形？
（3）在点Q从点B返回点A的运动过程中，设△PCQ的面积为s平方单位．
①求s与ι之间的函数关系式；
②当s最大时，过点P作直线交AB于点D，将△ABC中沿直线PD折叠，使点A落在直线PC上，求折叠后的
△APD与△PCQ重叠部分的面积．
（1）当t= 时，点P与点Q相遇；
（2）在点P从点B到点C的运动过程中，当ι为何值时，△PCQ为等腰三角形？
（3）在点Q从点B返回点A的运动过程中，设△PCQ的面积为s平方单位．
①求s与ι之间的函数关系式；
②当s最大时，过点P作直线交AB于点D，将△ABC中沿直线PD折叠，使点A落在直线PC上，求折叠后的
△APD与△PCQ重叠部分的面积．
