全一卷
1.化简 的结果是()
的结果是()
 的结果是()
的结果是()A. | B. | C. | D. |
2.代数式 的值为9,则
的值为9,则 的值为( )
的值为( )
 的值为9,则
的值为9,则 的值为( )
的值为( )A. | B. | C. | D. |
3.解分式方程 ,可知方程( )
,可知方程( )
 ,可知方程( )
,可知方程( )A.解为 | B.解为 | C.解为 | D.无解 |
4.小强、小亮、小文三位同学玩投硬币游戏.三人同时各投出一枚均匀硬币,若出现三个正面向上或三个反面向上,则小强赢;若出现2个正面向上一个反面向上,则小亮赢;若出现一个正面向上2个反面向上,则小文赢.下面说法正确的是( )
| A.小强赢的概率最小 | B.小文赢的概率最小 |
| C.小亮赢的概率最小 | D.三人赢的概率都相等 |
5.如图,两个全等的长方形 与
与 ,旋转长方形
,旋转长方形 能和长方形
能和长方形 重合,则可以作为旋转中心的点有()
重合,则可以作为旋转中心的点有()

 与
与 ,旋转长方形
,旋转长方形 能和长方形
能和长方形 重合,则可以作为旋转中心的点有()
重合,则可以作为旋转中心的点有()
| A.1个 | B.2个 | C.3个 | D.无数个 |
6.如图,国旗上的五角星的五个角的度数是相同的,每一个角的度数都是 ( )


A. | B. | C. | D. |
7.关于x一元二次方程 的一个根为1,p=( )
的一个根为1,p=( )
 的一个根为1,p=( )
的一个根为1,p=( )| A.4 | B.0或2 | C.1 | D.-1 |
8.某校初三共有四个班,在一次英语测试中四个班的平均分与各班参加人数如下表:
则本校初三参加这次英语测试的所有学生的平均分为( )(保留3个有效数字)
A.83.1 B.83.2 C.83.4 D.82.5
| 班级 | 一班 | 二班 | 三班 | 四班 |
| 参加人数 | 51 | 49 | 50 | 60 |
| 班平均分 | 83 | 89 | 82 | 79.5 |
A.83.1 B.83.2 C.83.4 D.82.5
9.如图,梯形 中,
中, ,
, ,
, ,
, ,则
,则 的长为()
的长为()

 中,
中, ,
, ,
, ,
, ,则
,则 的长为()
的长为()
A. | B. | C. | D. |
10.设 是函数
是函数 在第一象限的图像上任意一点,点
在第一象限的图像上任意一点,点 关于原点的对称点为
关于原点的对称点为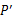 ,过
,过 作
作 平行于
平行于 轴,过
轴,过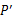 作
作 平行于
平行于 轴,
轴, 与
与 交于
交于 点,则
点,则 的面积()
的面积()

 是函数
是函数 在第一象限的图像上任意一点,点
在第一象限的图像上任意一点,点 关于原点的对称点为
关于原点的对称点为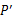 ,过
,过 作
作 平行于
平行于 轴,过
轴,过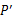 作
作 平行于
平行于 轴,
轴, 与
与 交于
交于 点,则
点,则 的面积()
的面积()
| A.等于2 | B.等于4 | C.等于8 | D.随 点的变化而变化 点的变化而变化 |
11.对于二次函数 ,我们把使函数值等于
,我们把使函数值等于 的实数
的实数 叫做这个函数的零点,则二次函数
叫做这个函数的零点,则二次函数 (
( 为实数)的零点的个数是()
为实数)的零点的个数是()
 ,我们把使函数值等于
,我们把使函数值等于 的实数
的实数 叫做这个函数的零点,则二次函数
叫做这个函数的零点,则二次函数 (
( 为实数)的零点的个数是()
为实数)的零点的个数是()| A.1 | B.2 | C.0 | D.不能确定 |
12.如图,矩形 的周长为
的周长为 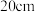 ,两条对角线相交于
,两条对角线相交于  点,过点
点,过点  作
作  的垂线
的垂线  ,分别交
,分别交  于
于  点,连结
点,连结  ,则
,则  的周长为( )
的周长为( )

 的周长为
的周长为 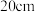 ,两条对角线相交于
,两条对角线相交于  点,过点
点,过点  作
作  的垂线
的垂线  ,分别交
,分别交  于
于  点,连结
点,连结  ,则
,则  的周长为( )
的周长为( )
| A.5cm | B.8cm | C.9cm | D.10cm |
13.在实数范围内分解因式:
_________ .

14.如图,以 为圆心的两个同心圆中,大圆的弦
为圆心的两个同心圆中,大圆的弦 是小圆的切线.若大圆半径为
是小圆的切线.若大圆半径为 ,小圆半径为
,小圆半径为 ,则弦
,则弦 的长为
的长为________ .

 为圆心的两个同心圆中,大圆的弦
为圆心的两个同心圆中,大圆的弦 是小圆的切线.若大圆半径为
是小圆的切线.若大圆半径为 ,小圆半径为
,小圆半径为 ,则弦
,则弦 的长为
的长为
15.观察下列等式:
 ;
;
 ;
;
 ;
;
 ;
;
……
用自然数 (其中
(其中 )表示上面一系列等式所反映出来的规律是
)表示上面一系列等式所反映出来的规律是__________ .
 ;
; ;
; ;
; ;
;……
用自然数
 (其中
(其中 )表示上面一系列等式所反映出来的规律是
)表示上面一系列等式所反映出来的规律是16.幼儿园把新购进的一批玩具分给小朋友.若每人3件,那么还剩余59件;若每人5件,那么最后一个小朋友分到玩具,但不足4件,这批玩具共有 件.
17.如图, 为半圆
为半圆 的直径,
的直径, 为
为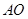 的中点,
的中点, 交半圆于点
交半圆于点 ,以
,以 为圆心,
为圆心, 为半径画弧
为半径画弧 交
交 于
于 点,若
点,若 ,则图中阴影部分的面积为
,则图中阴影部分的面积为_____  (取准确值).
(取准确值).

 为半圆
为半圆 的直径,
的直径, 为
为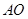 的中点,
的中点, 交半圆于点
交半圆于点 ,以
,以 为圆心,
为圆心, 为半径画弧
为半径画弧 交
交 于
于 点,若
点,若 ,则图中阴影部分的面积为
,则图中阴影部分的面积为 (取准确值).
(取准确值).
18.2006年潍坊市学业水平考试数学学科的考试成绩以等级公布.以县(市)为单位将所有考生成绩按由高到低分为 五个等级,五个等级所占比例依次为
五个等级,五个等级所占比例依次为 ,
, ,
, ,
, ,
, .小明所在学习小组随机抽查本学校2006年毕业学生,了解参加学业水平考试的考生数学成绩(等级)情况,统计如下表:
.小明所在学习小组随机抽查本学校2006年毕业学生,了解参加学业水平考试的考生数学成绩(等级)情况,统计如下表:
(1)根据小明所在学习小组抽查到的学生数学成绩五个等级人数的分布情况,绘制扇形统计图;
(2)根据小明所在学习小组的调查,估计2006年全校1320名参加数学考试的学生中,数学成绩(等级)为 等的考生各有多少人?
等的考生各有多少人?
(3)根据抽查结果,请你对小明所在学校参加2006年学业水平考试的数学成绩在全县(市)内的情况发表自己的看法.
 五个等级,五个等级所占比例依次为
五个等级,五个等级所占比例依次为 ,
, ,
, ,
, ,
, .小明所在学习小组随机抽查本学校2006年毕业学生,了解参加学业水平考试的考生数学成绩(等级)情况,统计如下表:
.小明所在学习小组随机抽查本学校2006年毕业学生,了解参加学业水平考试的考生数学成绩(等级)情况,统计如下表:| 成绩(等级) |  |  |  |  |  |
| 人数 | 16 | 20 | 24 | 12 | 8 |
(1)根据小明所在学习小组抽查到的学生数学成绩五个等级人数的分布情况,绘制扇形统计图;
(2)根据小明所在学习小组的调查,估计2006年全校1320名参加数学考试的学生中,数学成绩(等级)为
 等的考生各有多少人?
等的考生各有多少人?(3)根据抽查结果,请你对小明所在学校参加2006年学业水平考试的数学成绩在全县(市)内的情况发表自己的看法.
19.为改善办学条件,北海中学计划购买部分 品牌电脑和
品牌电脑和 品牌课桌.第一次,用9万元购买了
品牌课桌.第一次,用9万元购买了 品牌电脑10台和
品牌电脑10台和 品牌课桌200张.第二次,用9万元购买了
品牌课桌200张.第二次,用9万元购买了 品牌电脑12台和
品牌电脑12台和 品牌课桌120张.
品牌课桌120张.
(1)每台 品牌电脑与每张
品牌电脑与每张 品牌课桌的价格各是多少元?
品牌课桌的价格各是多少元?
(2)第三次购买时,销售商对一次购买量大的客户打折销售.规定:一次购买 品牌电脑35台以上(含35台),按九折销售,一次购买
品牌电脑35台以上(含35台),按九折销售,一次购买 品牌课桌600张以上(含600张),按八折销售.学校准备用27万元购买电脑和课桌,其中电脑不少于35台,课桌不少于600张,问有几种购买方案?
品牌课桌600张以上(含600张),按八折销售.学校准备用27万元购买电脑和课桌,其中电脑不少于35台,课桌不少于600张,问有几种购买方案?
 品牌电脑和
品牌电脑和 品牌课桌.第一次,用9万元购买了
品牌课桌.第一次,用9万元购买了 品牌电脑10台和
品牌电脑10台和 品牌课桌200张.第二次,用9万元购买了
品牌课桌200张.第二次,用9万元购买了 品牌电脑12台和
品牌电脑12台和 品牌课桌120张.
品牌课桌120张.(1)每台
 品牌电脑与每张
品牌电脑与每张 品牌课桌的价格各是多少元?
品牌课桌的价格各是多少元?(2)第三次购买时,销售商对一次购买量大的客户打折销售.规定:一次购买
 品牌电脑35台以上(含35台),按九折销售,一次购买
品牌电脑35台以上(含35台),按九折销售,一次购买 品牌课桌600张以上(含600张),按八折销售.学校准备用27万元购买电脑和课桌,其中电脑不少于35台,课桌不少于600张,问有几种购买方案?
品牌课桌600张以上(含600张),按八折销售.学校准备用27万元购买电脑和课桌,其中电脑不少于35台,课桌不少于600张,问有几种购买方案?20.如图,某居民小区内 两楼之间的距离
两楼之间的距离 米,两楼的高都是20米,
米,两楼的高都是20米, 楼在
楼在 楼正南,
楼正南, 楼窗户朝南.
楼窗户朝南. 楼内一楼住户的窗台离小区地面的距离
楼内一楼住户的窗台离小区地面的距离 米,窗户高
米,窗户高 米.当正午时刻太阳光线与地面成
米.当正午时刻太阳光线与地面成 角时,
角时, 楼的影子是否影响
楼的影子是否影响 楼的一楼住户采光?若影响,挡住该住户窗户多高?若不影响,请说明理由.
楼的一楼住户采光?若影响,挡住该住户窗户多高?若不影响,请说明理由.
(参考数据: ,
, ,
, )
)

 两楼之间的距离
两楼之间的距离 米,两楼的高都是20米,
米,两楼的高都是20米, 楼在
楼在 楼正南,
楼正南, 楼窗户朝南.
楼窗户朝南. 楼内一楼住户的窗台离小区地面的距离
楼内一楼住户的窗台离小区地面的距离 米,窗户高
米,窗户高 米.当正午时刻太阳光线与地面成
米.当正午时刻太阳光线与地面成 角时,
角时, 楼的影子是否影响
楼的影子是否影响 楼的一楼住户采光?若影响,挡住该住户窗户多高?若不影响,请说明理由.
楼的一楼住户采光?若影响,挡住该住户窗户多高?若不影响,请说明理由.(参考数据:
 ,
, ,
, )
)
21.蔬菜基地种植某种蔬菜,由市场行情分析知,1月份至6月份这种蔬菜的上市时间 (月份)与市场售价
(月份)与市场售价 (元/千克)的关系如下表:
(元/千克)的关系如下表:
这种蔬菜每千克的种植成本 (元/千克)与上市时间
(元/千克)与上市时间 (月份)满足一个函数关系,这个函数的图象是抛物线的一段(如图).
(月份)满足一个函数关系,这个函数的图象是抛物线的一段(如图).
(1)写出上表中表示的市场售价 (元/千克)关于上市时间
(元/千克)关于上市时间 (月份)的函数关系式;
(月份)的函数关系式;
(2)若图中抛物线过 点,写出抛物线对应的函数关系式;
点,写出抛物线对应的函数关系式;
(3)由以上信息分析,哪个月上市出售这种蔬菜每千克的收益最大?最大值为多少?(收益=市场售价-种植成本)

 (月份)与市场售价
(月份)与市场售价 (元/千克)的关系如下表:
(元/千克)的关系如下表:上市时间 (月份) (月份) | 1 | 2 | 3 | 4 | 5 | 6 |
市场售价 (元/千克) (元/千克) | 10.5 | 9 | 7.5 | 6 | 4.5 | 3 |
 (元/千克)与上市时间
(元/千克)与上市时间 (月份)满足一个函数关系,这个函数的图象是抛物线的一段(如图).
(月份)满足一个函数关系,这个函数的图象是抛物线的一段(如图).(1)写出上表中表示的市场售价
 (元/千克)关于上市时间
(元/千克)关于上市时间 (月份)的函数关系式;
(月份)的函数关系式;(2)若图中抛物线过
 点,写出抛物线对应的函数关系式;
点,写出抛物线对应的函数关系式;(3)由以上信息分析,哪个月上市出售这种蔬菜每千克的收益最大?最大值为多少?(收益=市场售价-种植成本)

22.如图1,线段 过圆心
过圆心 ,交圆
,交圆 于
于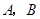 两点,
两点,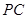 切圆
切圆 于点
于点 ,作
,作 ,垂足为
,垂足为 ,连结
,连结 .
.
(1)写出图1中所有相等的角(直角除外),并给出证明;
(2)若图1中的切线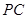 变为图2中割线
变为图2中割线 的情形,
的情形, 与圆
与圆 交于
交于 两点,
两点,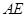 与
与 交于点
交于点 ,
, ,写出图2中相等的角(写出三组即可,直角除外);
,写出图2中相等的角(写出三组即可,直角除外);
(3)在图2中,证明: .
.

 过圆心
过圆心 ,交圆
,交圆 于
于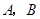 两点,
两点,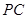 切圆
切圆 于点
于点 ,作
,作 ,垂足为
,垂足为 ,连结
,连结 .
.(1)写出图1中所有相等的角(直角除外),并给出证明;
(2)若图1中的切线
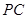 变为图2中割线
变为图2中割线 的情形,
的情形, 与圆
与圆 交于
交于 两点,
两点,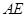 与
与 交于点
交于点 ,
, ,写出图2中相等的角(写出三组即可,直角除外);
,写出图2中相等的角(写出三组即可,直角除外);(3)在图2中,证明:
 .
.

23.已知等腰 中,
中, ,
, 平分
平分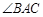 交
交 于
于 点,在线段
点,在线段 上任取一点
上任取一点 (
( 点除外),过
点除外),过 点作
点作 ,分别交
,分别交 于
于 点,作
点,作 ,交
,交 于
于 点,连结
点,连结 .
.
(1)求证:四边形 为菱形;
为菱形;
(2)当 点在何处时,菱形
点在何处时,菱形 的面积为四边形
的面积为四边形 面积的一半?
面积的一半?
 中,
中, ,
, 平分
平分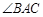 交
交 于
于 点,在线段
点,在线段 上任取一点
上任取一点 (
( 点除外),过
点除外),过 点作
点作 ,分别交
,分别交 于
于 点,作
点,作 ,交
,交 于
于 点,连结
点,连结 .
.(1)求证:四边形
 为菱形;
为菱形;(2)当
 点在何处时,菱形
点在何处时,菱形 的面积为四边形
的面积为四边形 面积的一半?
面积的一半?
24.如图,已知平面直角坐标系 中,点
中,点 ,
, 为两动点,其中
为两动点,其中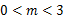 ,连结
,连结 ,
, .
.
(1)求证: ;
;
(2)当 时,抛物线经过
时,抛物线经过 两点且以
两点且以 轴为对称轴,求抛物线对应的二次函数的关系式;
轴为对称轴,求抛物线对应的二次函数的关系式;
(3)在(2)的条件下,设直线 交
交 轴于点
轴于点 ,过点
,过点 作直线
作直线 交抛物线于
交抛物线于 两点,问是否存在直线
两点,问是否存在直线 ,使
,使 ?若存在,求出直线
?若存在,求出直线 对应的函数关系式;若不存在,请说明理由.
对应的函数关系式;若不存在,请说明理由.
 中,点
中,点 ,
, 为两动点,其中
为两动点,其中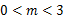 ,连结
,连结 ,
, .
.(1)求证:
 ;
;(2)当
 时,抛物线经过
时,抛物线经过 两点且以
两点且以 轴为对称轴,求抛物线对应的二次函数的关系式;
轴为对称轴,求抛物线对应的二次函数的关系式;(3)在(2)的条件下,设直线
 交
交 轴于点
轴于点 ,过点
,过点 作直线
作直线 交抛物线于
交抛物线于 两点,问是否存在直线
两点,问是否存在直线 ,使
,使 ?若存在,求出直线
?若存在,求出直线 对应的函数关系式;若不存在,请说明理由.
对应的函数关系式;若不存在,请说明理由.
 搜索
搜索
 难度系数:0.94
难度系数:0.94  答案解析
答案解析
 有奖纠错
有奖纠错
