搜索
全一卷
难度系数：0.85 
答案解析
有奖纠错
1．－5的相反数是_________ ，4的平方根是__________ .
2．分解因式：
－x=__________ ．
－x=3．我市2004年一季度城镇居民人均消费支出约2500元，这个数据用科学记数法可表示为___________ 元．
4．设x1、x2是方程
的两个实数根，则x1+x2=_____ ；x1·x2=_____ .
的两个实数根，则x1+x2=5．函数y=
中，自变量x的取值范围是___________ ；
中，自变量x的取值范围是6．函数y=
中，自变量x的取值范围是____________ ．
中，自变量x的取值范围是7．反比例函数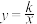
的图象经过点（2，－1），则k的值为______ .
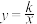的图象经过点（2，－1），则k的值为8．一射击运动员在一次射击练习中打出的成绩是（单位：环）：7，8，9，8，6，8，10，7，这组数据的众数是_________.
9．如图，P是∠AOB的平分线上的一点，PC⊥AO于C，PD⊥OB于D，写出图中一组相等的线段__________ （只需写出一组即可）
10．用同一种正多边形地砖镶嵌成平整的地面，那么这种正多边形地砖的形状可以是________ . （只需写出一种即可）
11．若梯形的面积为6㎝2，高为2㎝，则此梯形地中位线长为_________ ㎝.
12．如图，AB是⊙O的直径，若AB=4㎝，∠D=30°，则∠B=______ °，AC=___ ㎝.
13．某商场为了解本商场的服务质量，随机调查了本商场的100名顾客，调查的结果如图所示，根据图中给出的信息，这100名顾客中对该商场的服务质量表示不满意的有____ 人
14．一跳蚤在一直线上从O点开始，第1次向右跳1个单位，紧接着第2次向左跳2个单位，第3次向右跳3个单位，第4次向左跳4个单位，……，依此规律跳下去，当它跳第100次落下时，落点处离O点的距离是_______ 个单位．
15．下列各式中，与
是同类项的是（ ）
是同类项的是（ ）A． | B．2xy | C．－ | D． |
16．比较
的大小，结果正确的是（）
的大小，结果正确的是（）A． | B． | C． | D． |
17．一元二次方程
的根为（）
的根为（）A． | B． | C． | D． |
18．已知⊙O1与⊙O2的半径分别为2和4，圆心距O1O2=6，则这两圆的位置关系是（）
| A．相离 | B．外切 | C．相交 | D．内切 |
19．下列调查中，适合用普查方法的是（ ）
| A．电视机厂要了解一批显象管的使用寿命 |
| B．要了解我市居民的环保意识 |
| C．要了解我市“阳山水蜜桃”的甜度和含水量 |
| D．要了解你校数学教师的年龄状况 |
20．下列事件中，属于必然事件的是（）
| A．明天我市下雨 |
| B．我走出校门，看到的第一辆汽车的牌照的末位数字是偶数 |
| C．抛一枚硬币，正面朝上 |
| D．一口袋中装有2个红球和1个白球，从中摸出2个球，其中有红球 |
21．一个几何体的三视图如图所示，则这个几何体是( )
| A．圆柱 | B．圆锥 | C．长方体 | D．正方体 |
22．如图是一个正四面体，它的四个面都是正三角形，现沿它的三条棱AC、BC、CD剪开展成平面图形，则所得的展开图是（）
A． | B． | C． | D． |
23．计算：
；
；24．解不等式组
25．已知：如图，平行四边形ABCD中，E、F分别是边BC和AD上的点，且BE=DF，求证：AE=CF
26．已知图1和图2中的每个小正方形的边长都是1个单位.
（1）将图1中的格点△ABC，先向右平移3个单位，再向上平移2个单位，得到△A1B1C1，请你在图1中画出△A1B1C1.
（2）在图2中画出一个与格点△DEF相似但相似比不等于1的格点三角形.
（1）将图1中的格点△ABC，先向右平移3个单位，再向上平移2个单位，得到△A1B1C1，请你在图1中画出△A1B1C1.
（2）在图2中画出一个与格点△DEF相似但相似比不等于1的格点三角形.
27．四张大小、质地均相同的卡片上分别标有数字1，2，3，4，现将标有数字的一面朝下扣在桌子上，从中随机抽取一张（不放回），再从桌子上剩下的3张中随机抽取第二张.
（1）用画树状图的方法，列出前后两次抽得的卡片上所标数字的所有可能情况；
（2）计算抽得的两张卡片上的数字之积为奇数的概率是多少？
（1）用画树状图的方法，列出前后两次抽得的卡片上所标数字的所有可能情况；
（2）计算抽得的两张卡片上的数字之积为奇数的概率是多少？
28．甲、乙两人在某公司做见习推销员，推销“小天鹅”洗衣机，他们在1～8月份的销售情况如下表所示：
（1）在右边给出的坐标系中，绘制甲、乙两人这8个月的月销售量的折线图：（甲用实线；乙用虚线）
（2）请根据（1）中的折线图，写出2条关于甲、乙两人在这8个月中的销售状况的信息.
① ；② .
（1）在右边给出的坐标系中，绘制甲、乙两人这8个月的月销售量的折线图：（甲用实线；乙用虚线）
（2）请根据（1）中的折线图，写出2条关于甲、乙两人在这8个月中的销售状况的信息.
① ；② .
29．某天，一蔬菜经营户用60元钱从蔬菜批发市场批了西红柿和豆角共40㎏到菜市场去卖，西红柿和豆角这天的批发价与零售价如下表所示：
问：他当天卖完这些西红柿和豆角能赚多少钱？
问：他当天卖完这些西红柿和豆角能赚多少钱？
30．如图，一次函数
的图象与x轴和y轴分别交于点A（6，0）和B（0，
），线段AB的垂直平分线交x轴于点C，交AB于点D.
（1）试确定这个一次函数关系式；
（2）求过A、B、C三点的抛物线的函数关系式.
的图象与x轴和y轴分别交于点A（6，0）和B（0，
），线段AB的垂直平分线交x轴于点C，交AB于点D.（1）试确定这个一次函数关系式；
（2）求过A、B、C三点的抛物线的函数关系式.
31．如图，已知矩形ABCD的边长AB=2，BC=3，点P是AD边上的一动点（P异于A、D），Q是BC边上的任意一点. 连AQ、DQ，过P作PE∥DQ交AQ于E，作PF∥AQ交DQ于
A． （1）求证：△APE∽△ADQ； （2）设AP的长为x，试求△PEF的面积S△PEF关于x的函数关系式，并求当P在何处时，S△PEF取得最大值？最大值为多少？ （3）当Q在何处时，△ADQ的周长最小？（须给出确定Q在何处的过程或方法，不必给出证明） |
32．已知，点P是正方形ABCD内的一点，连PA、PB、P
| A． （1）将△PAB绕点B顺时针旋转90°到△P′CB的位置（如图1）. ①设AB的长为a，PB的长为b（b<a），求△PAB旋转到△P′CB的过程中边PA所扫过区域（图1中阴影部分）的面积； ②若PA=2，PB=4，∠APB=135°，求PC的长. （2）如图2，若PA2+PC2=2PB2，请说明点P必在对角线AC上.  |
33．已知正方形ABCD的边长AB=k（k是正整数），正△PAE的顶点P在正方形内，顶点E在边AB上，且AE="1." 将△PAE在正方形内按图1中所示的方式，沿着正方形的边AB、BC、CD、DA、AB、……连续地翻转n次，使顶点P第一次回到原来的起始位置.
（1）如果我们把正方形ABCD的边展开在一直线上，那么这一翻转过程可以看作是△PAE在直线上作连续的翻转运动. 图2是k=1时，△PAE沿正方形的边连续翻转过程的展开示意图. 请你探索：若k=1，则△PAE沿正方形的边连续翻转的次数n= 时，顶点P第一次回到原来的起始位置.
（2）若k=2，则n= 时，顶点P第一次回到原来的起始位置；若k=3，则n= 时，顶点P第一次回到原来的起始位置.
（3）请你猜测：使顶点P第一次回到原来的起始位置的n值与k之间的关系（请用含k的代数式表示n）.
（1）如果我们把正方形ABCD的边展开在一直线上，那么这一翻转过程可以看作是△PAE在直线上作连续的翻转运动. 图2是k=1时，△PAE沿正方形的边连续翻转过程的展开示意图. 请你探索：若k=1，则△PAE沿正方形的边连续翻转的次数n= 时，顶点P第一次回到原来的起始位置.
（2）若k=2，则n= 时，顶点P第一次回到原来的起始位置；若k=3，则n= 时，顶点P第一次回到原来的起始位置.
（3）请你猜测：使顶点P第一次回到原来的起始位置的n值与k之间的关系（请用含k的代数式表示n）.
