全一卷
1. 等于( )
等于( )
 等于( )
等于( )A. | B. | C. | D. |
2.化简 的结果是( )
的结果是( )
 的结果是( )
的结果是( )A. | B. | C. | D. |
3.在数轴上表示不等式 的解集,正确的是( )
的解集,正确的是( )
 的解集,正确的是( )
的解集,正确的是( )A. | B. | C. | D. |
4.如图,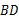 为
为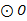 的直径,
的直径, ,则
,则 的度数为()
的度数为()

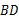 为
为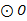 的直径,
的直径, ,则
,则 的度数为()
的度数为()
A. | B. | C. | D. |
5.从某班学生中随机选取一名学生是女生的概率为 ,则该班女生与男生的人数比是( )
,则该班女生与男生的人数比是( )
 ,则该班女生与男生的人数比是( )
,则该班女生与男生的人数比是( )A. | B. | C. | D. |
6.由6个大小相同的正方体搭成的几何体如图所示,则关于它的视图说法正确的是( )


| A.正视图的面积最大 | B.左视图的面积最大 |
| C.俯视图的面积最大 | D.三个视图的面积一样大 |
7.如图,双曲线 的一个分支为( )
的一个分支为( )

 的一个分支为( )
的一个分支为( )
| A.① | B.② | C.③ | D.④ |
8.如图,将圆桶中的水倒入一个直径为 ,高为
,高为 的圆口容器中,圆桶放置的角度与水平线的夹角为
的圆口容器中,圆桶放置的角度与水平线的夹角为 .若使容器中的水面与圆桶相接触,则容器中水的深度至少应为()
.若使容器中的水面与圆桶相接触,则容器中水的深度至少应为()

 ,高为
,高为 的圆口容器中,圆桶放置的角度与水平线的夹角为
的圆口容器中,圆桶放置的角度与水平线的夹角为 .若使容器中的水面与圆桶相接触,则容器中水的深度至少应为()
.若使容器中的水面与圆桶相接触,则容器中水的深度至少应为()
A. | B. | C. | D. |
9.计算:
____ .

10.函数 的图象经过点
的图象经过点 ,则
,则 的值为
的值为____ .
 的图象经过点
的图象经过点 ,则
,则 的值为
的值为11.5名同学目测同一本教科书的宽度时,产生的误差如下(单位:cm): ,
,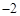 ,
,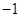 ,
,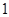 ,
, ,则这组数据的极差为
,则这组数据的极差为____ cm.
 ,
,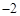 ,
,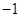 ,
,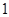 ,
, ,则这组数据的极差为
,则这组数据的极差为12.图中
__________ .



13.两圆有多种位置关系,图中不存在的位置关系是 .

14.如图,将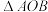 绕点
绕点 逆时针旋转
逆时针旋转 ,得到
,得到 .若点A的坐标为
.若点A的坐标为 ,则点
,则点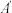 的坐标为
的坐标为_____ .

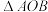 绕点
绕点 逆时针旋转
逆时针旋转 ,得到
,得到 .若点A的坐标为
.若点A的坐标为 ,则点
,则点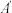 的坐标为
的坐标为
15.将直尺与三角尺按如图所示的方式叠放在一起.在图中标记的角中,写出所有与 互余的角.
互余的角.
 互余的角.
互余的角.
16.计算: .
.
 .
.17.下面的两个网格中,每个小正方形的边长均为 .请你分别在每个网格中画出一个顶点在格点上,且周长为
.请你分别在每个网格中画出一个顶点在格点上,且周长为 的形状和大小不同的凸多边形.
的形状和大小不同的凸多边形.
 .请你分别在每个网格中画出一个顶点在格点上,且周长为
.请你分别在每个网格中画出一个顶点在格点上,且周长为 的形状和大小不同的凸多边形.
的形状和大小不同的凸多边形.
18.小刚想给小东打电话,但忘了电话号码中的一位数字,只记得号码是 (
( 表示忘记的数字).
表示忘记的数字).
(1)若小刚从 至
至 的自然数中随机选取一个数放在
的自然数中随机选取一个数放在 位置,则他拨对小东电话号码的概率是 .
位置,则他拨对小东电话号码的概率是 .
(2)若 位置的数字是不等式组
位置的数字是不等式组 的整数解,求
的整数解,求 可能表示的数字.
可能表示的数字.
 (
( 表示忘记的数字).
表示忘记的数字).(1)若小刚从
 至
至 的自然数中随机选取一个数放在
的自然数中随机选取一个数放在 位置,则他拨对小东电话号码的概率是 .
位置,则他拨对小东电话号码的概率是 .(2)若
 位置的数字是不等式组
位置的数字是不等式组 的整数解,求
的整数解,求 可能表示的数字.
可能表示的数字.19.某服装厂准备加工300套演出服.在加工60套后,采用了新技术,使每天的工作效率是原来的2倍,结果共用9天完成任务.求该厂原来每天加工多少套演出服.
20.如图,矩形 是供一辆机动车停放的车位示意图.请你参考图中数据,计算车位所占街道的宽度
是供一辆机动车停放的车位示意图.请你参考图中数据,计算车位所占街道的宽度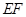 .
.
(参考数据: ,结果精确到
,结果精确到 .)
.)
 是供一辆机动车停放的车位示意图.请你参考图中数据,计算车位所占街道的宽度
是供一辆机动车停放的车位示意图.请你参考图中数据,计算车位所占街道的宽度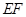 .
.(参考数据:
 ,结果精确到
,结果精确到 .)
.)
21.如图, 为抛物线
为抛物线 上对称轴右侧的一点,且点
上对称轴右侧的一点,且点 在
在 轴上方,过点
轴上方,过点 作
作 垂直
垂直 轴于点
轴于点 ,
, 垂直
垂直 轴于点
轴于点 ,得到矩形
,得到矩形 .若
.若 ,求矩形
,求矩形 的面积.
的面积.
 为抛物线
为抛物线 上对称轴右侧的一点,且点
上对称轴右侧的一点,且点 在
在 轴上方,过点
轴上方,过点 作
作 垂直
垂直 轴于点
轴于点 ,
, 垂直
垂直 轴于点
轴于点 ,得到矩形
,得到矩形 .若
.若 ,求矩形
,求矩形 的面积.
的面积.
22.某班组织一次数学测试,全班学生成绩的分布情况如下图:

(1)全班学生数学成绩的众数是 分,全班学生数学成绩为众数的有 人.
(2)全班学生数学成绩的中位数是 分.
(3)分别计算两个小组超过全班数学成绩中位数的人数占全班人数的百分比.

(1)全班学生数学成绩的众数是 分,全班学生数学成绩为众数的有 人.
(2)全班学生数学成绩的中位数是 分.
(3)分别计算两个小组超过全班数学成绩中位数的人数占全班人数的百分比.
23.如图, 为正比例函数
为正比例函数 图象上的一个动点,
图象上的一个动点, 的半径为
的半径为 ,设点
,设点 的坐标为
的坐标为 .
.

(1)求 与直线
与直线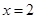 相切时点
相切时点 的坐标.
的坐标.
(2)请直接写出 与直线
与直线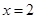 相交、相离时
相交、相离时 的取值范围.
的取值范围.
 为正比例函数
为正比例函数 图象上的一个动点,
图象上的一个动点, 的半径为
的半径为 ,设点
,设点 的坐标为
的坐标为 .
.
(1)求
 与直线
与直线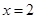 相切时点
相切时点 的坐标.
的坐标.(2)请直接写出
 与直线
与直线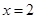 相交、相离时
相交、相离时 的取值范围.
的取值范围.24.如图,在 中,
中, 为
为 边上一点,且
边上一点,且 .
.

(1)求证: .
.
(2)若 平分
平分 ,
, ,求
,求 的度数.
的度数.
 中,
中, 为
为 边上一点,且
边上一点,且 .
.
(1)求证:
 .
.(2)若
 平分
平分 ,
, ,求
,求 的度数.
的度数.25.小张骑车往返于甲、乙两地,距甲地的路程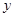 (千米)与时间
(千米)与时间 (小时)的函数图象如图所示.
(小时)的函数图象如图所示.

(1)小张在路上停留 小时,他从乙地返回时骑车的速度为 千米/时.(3分)
(2)小李与小张同时从甲地出发,按相同路线匀速前往乙地,到乙地停止,途中小李与小张共相遇3次.请在图中画出小李距甲地的路程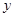 (千米)与时间
(千米)与时间 (小时)的函数的大致图象.(3分)
(小时)的函数的大致图象.(3分)
(3)小王与小张同时出发,按相同路线前往乙地,距甲地的路程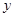 (千米)与时间
(千米)与时间 (小时)的函数关系式为
(小时)的函数关系式为 .小王与小张在途中共相遇几次?请你计算第一次相遇的时间.(4分)
.小王与小张在途中共相遇几次?请你计算第一次相遇的时间.(4分)
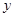 (千米)与时间
(千米)与时间 (小时)的函数图象如图所示.
(小时)的函数图象如图所示.
(1)小张在路上停留 小时,他从乙地返回时骑车的速度为 千米/时.(3分)
(2)小李与小张同时从甲地出发,按相同路线匀速前往乙地,到乙地停止,途中小李与小张共相遇3次.请在图中画出小李距甲地的路程
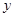 (千米)与时间
(千米)与时间 (小时)的函数的大致图象.(3分)
(小时)的函数的大致图象.(3分)(3)小王与小张同时出发,按相同路线前往乙地,距甲地的路程
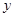 (千米)与时间
(千米)与时间 (小时)的函数关系式为
(小时)的函数关系式为 .小王与小张在途中共相遇几次?请你计算第一次相遇的时间.(4分)
.小王与小张在途中共相遇几次?请你计算第一次相遇的时间.(4分)26.如图①,正方形 的顶点
的顶点 的坐标分别为
的坐标分别为 ,顶点
,顶点 在第一象限.点
在第一象限.点 从点
从点 出发,沿正方形按逆时针方向匀速运动,同时,点
出发,沿正方形按逆时针方向匀速运动,同时,点 从点
从点 出发,沿
出发,沿 轴正方向以相同速度运动.当点
轴正方向以相同速度运动.当点 到达点
到达点 时,
时, 两点同时停止运动,设运动的时间为
两点同时停止运动,设运动的时间为 秒.
秒.

(1)求正方形 的边长.
的边长.
(2)当点 在
在 边上运动时,
边上运动时, 的面积
的面积 (平方单位)与时间
(平方单位)与时间 (秒)之间的函数图象为抛物线的一部分(如图②所示),求
(秒)之间的函数图象为抛物线的一部分(如图②所示),求 两点的运动速度.
两点的运动速度.
(3)求(2)中面积 (平方单位)与时间
(平方单位)与时间 (秒)的函数关系式及面积
(秒)的函数关系式及面积 取最大值时点
取最大值时点 的坐标.
的坐标.
(4)若点 保持(2)中的速度不变,则点
保持(2)中的速度不变,则点 沿着
沿着 边运动时,
边运动时, 的大小随着时间
的大小随着时间 的增大而增大;沿着
的增大而增大;沿着 边运动时,
边运动时, 的大小随着时间
的大小随着时间 的增大而减小.当点
的增大而减小.当点 沿着这两边运动时,使
沿着这两边运动时,使 的点
的点 有 个.
有 个.
(抛物线 的顶点坐标是
的顶点坐标是 .)
.)
 的顶点
的顶点 的坐标分别为
的坐标分别为 ,顶点
,顶点 在第一象限.点
在第一象限.点 从点
从点 出发,沿正方形按逆时针方向匀速运动,同时,点
出发,沿正方形按逆时针方向匀速运动,同时,点 从点
从点 出发,沿
出发,沿 轴正方向以相同速度运动.当点
轴正方向以相同速度运动.当点 到达点
到达点 时,
时, 两点同时停止运动,设运动的时间为
两点同时停止运动,设运动的时间为 秒.
秒.
(1)求正方形
 的边长.
的边长.(2)当点
 在
在 边上运动时,
边上运动时, 的面积
的面积 (平方单位)与时间
(平方单位)与时间 (秒)之间的函数图象为抛物线的一部分(如图②所示),求
(秒)之间的函数图象为抛物线的一部分(如图②所示),求 两点的运动速度.
两点的运动速度.(3)求(2)中面积
 (平方单位)与时间
(平方单位)与时间 (秒)的函数关系式及面积
(秒)的函数关系式及面积 取最大值时点
取最大值时点 的坐标.
的坐标.(4)若点
 保持(2)中的速度不变,则点
保持(2)中的速度不变,则点 沿着
沿着 边运动时,
边运动时, 的大小随着时间
的大小随着时间 的增大而增大;沿着
的增大而增大;沿着 边运动时,
边运动时, 的大小随着时间
的大小随着时间 的增大而减小.当点
的增大而减小.当点 沿着这两边运动时,使
沿着这两边运动时,使 的点
的点 有 个.
有 个.(抛物线
 的顶点坐标是
的顶点坐标是 .)
.) 搜索
搜索
 难度系数:0.94
难度系数:0.94  答案解析
答案解析
 有奖纠错
有奖纠错
