全一卷
1.计算:22=()
| A.1 | B.2 | C.4 | D.8 |
2.如图,a // b, c 与a ,b都相交,∠1=50°,则∠2="(" )


| A.40° | B.50° | C.100° | D.130° |
3.计算:

| A.3 | B. | C.2 | D.4 |
4.下列基本几何体中,三视图都是相同图形的是()
A. | B. | C. | D. |
5.正六边形的每个内角都是( )
| A.60° | B.80° | C.100° | D.120° |
6.市农科所收集统计了甲、乙两种甜玉米各10块试验田的亩产量后,得到其方差分别是 、
、 ,则()
,则()
 、
、 ,则()
,则()| A.甲比乙的亩产量稳定 | B.乙比甲的亩产量稳定 |
| C.甲、乙的亩产量的稳定性相同 | D.无法确定哪一种的亩产量更稳定 |
7.一次函数 的图象过点(0,2),且 y随x的增大而增大,则m=( )
的图象过点(0,2),且 y随x的增大而增大,则m=( )
 的图象过点(0,2),且 y随x的增大而增大,则m=( )
的图象过点(0,2),且 y随x的增大而增大,则m=( )| A.-1 | B.3 | C.1 | D.-1或3 |
8.如图,在菱形ABCD中,对角线AC,BD相交于点O,且AC≠BD,则图中全等三角形有()


| A.4对 | B.6对. | C.8对 | D.10对 |
9.如图,Rt△ABC的内切圆⊙O与两直角边AB,BC分别相切于点D,E,过劣弧DE(不包括端点D,E)上任一点P作⊙O的切线MN,与AB,BC分别交于点M,N,若⊙O的半径为r,则Rt△MBN的周长为( )


| A.r | B. r r | C.2r | D. r r |
10.如图,正方形ABCD的两边BC,AB分别在平面直角坐标系的 轴、
轴、 轴的正半轴上,正方形A′B′C′D′与正方形ABCD是以AC的中点O′为中心的位似图形,已知AC=
轴的正半轴上,正方形A′B′C′D′与正方形ABCD是以AC的中点O′为中心的位似图形,已知AC= ,若点A′的坐标为(1,2),则正方形A′B′C′D′与正方形ABCD的相似比是( )
,若点A′的坐标为(1,2),则正方形A′B′C′D′与正方形ABCD的相似比是( )

 轴、
轴、 轴的正半轴上,正方形A′B′C′D′与正方形ABCD是以AC的中点O′为中心的位似图形,已知AC=
轴的正半轴上,正方形A′B′C′D′与正方形ABCD是以AC的中点O′为中心的位似图形,已知AC= ,若点A′的坐标为(1,2),则正方形A′B′C′D′与正方形ABCD的相似比是( )
,若点A′的坐标为(1,2),则正方形A′B′C′D′与正方形ABCD的相似比是( )
A. | B. | C. | D. |
11.二次函数 (
( ≠0)的图像如图所示,其对称轴为
≠0)的图像如图所示,其对称轴为 =1,有如下结论:①
=1,有如下结论:① <1 ②2
<1 ②2 +
+ ="0" ③
="0" ③ <4
<4
 ④若方程
④若方程 的两个根为
的两个根为 ,
, ,则
,则 +
+ =2.则结论正确的是()
=2.则结论正确的是()

 (
( ≠0)的图像如图所示,其对称轴为
≠0)的图像如图所示,其对称轴为 =1,有如下结论:①
=1,有如下结论:① <1 ②2
<1 ②2 +
+ ="0" ③
="0" ③ <4
<4
 ④若方程
④若方程 的两个根为
的两个根为 ,
, ,则
,则 +
+ =2.则结论正确的是()
=2.则结论正确的是()
| A.①② | B.①③ | C.②④ | D.③④ |
12.一个盒子里有完全相同的三个小球,球上分别标有数字-1、1、2.随机摸出一个小球(不放回)其数字记为P ,再随机摸出另一个小球其数字记为q ,则满足关于的方程 有实数根的概率是()
有实数根的概率是()
 有实数根的概率是()
有实数根的概率是()A. | B. | C. | D. |
13.既不是正数也不是负数的数是_____
14.某种原子直径为1.2×10﹣2纳米,把这个数化为小数是__纳米.
15.在平面直角坐标系中,一青蛙从点A(-1,0)处向右跳2个单位长度,再向上跳2个单位长度到点A′处,则点A′的坐标为________ .
16.如图,矩形OABC内接于扇形MON,当CN=CO时,∠NMB的度数是________


17.如图,两块相同的三角板完全重合在一起,∠A=30°,AC=10,把上面一块绕直角顶点B逆时针旋转到△A′BC′的位置,点C′在AC上,A′C ′与AB相交于点D,则C′D=______ .


18.二次函数 的图像与
的图像与 轴围成的封闭区域内(包括边界),横、纵坐标都是整数的点有
轴围成的封闭区域内(包括边界),横、纵坐标都是整数的点有_______ 个(提示:必要时可利用下面的备用图画出图像来分析).

 的图像与
的图像与 轴围成的封闭区域内(包括边界),横、纵坐标都是整数的点有
轴围成的封闭区域内(包括边界),横、纵坐标都是整数的点有
19.计算: .
.
 .
.20.求不等式组 的整数解.
的整数解.
 的整数解.
的整数解.21.已知等腰△ABC的顶角∠A=36°(如图).

(1)作底角∠ABC的平分线BD,交AC于点D(用尺规作图,不写作法,但保留作图痕迹,然后用墨水笔加黑);
(2)通过计算说明△ABD和△BDC都是等腰三角形.

(1)作底角∠ABC的平分线BD,交AC于点D(用尺规作图,不写作法,但保留作图痕迹,然后用墨水笔加黑);
(2)通过计算说明△ABD和△BDC都是等腰三角形.
22.某奶品生产企业,2010年对铁锌牛奶、酸牛奶、纯牛奶三个品种的生产情况进行了统计,绘制了图1、2的统计图,请根据图中信息解答下列问题:
(1)酸牛奶生产了多少万吨?把图1补充完整;酸牛奶在图2中所对的圆心角是多少度?
(2)由于市场不断需求,据统计,2011年酸牛奶的生产量比2010年增长20%,按照这样的增长速度,请你估算2012年酸牛奶的生产量是多少万吨?
(1)酸牛奶生产了多少万吨?把图1补充完整;酸牛奶在图2中所对的圆心角是多少度?
(2)由于市场不断需求,据统计,2011年酸牛奶的生产量比2010年增长20%,按照这样的增长速度,请你估算2012年酸牛奶的生产量是多少万吨?

23.如图,已知点O为Rt△ABC斜边上一点,以点O为圆心,OA长为半径的⊙O与BC相切于点E,与AC相交于点D ,连接AE.(1)求证:AE平分∠CAB;
(2)探求图中∠1与∠C的数量关系,并求当AE=EC时tanC的值.
(2)探求图中∠1与∠C的数量关系,并求当AE=EC时tanC的值.

24.一工地计划租用甲、乙两辆车清理淤泥,从运输量来估算:若租两车合运,10天可以完成任务;若单独租用乙车完成任务则比单独租用甲车完成任务多用15天.
(1)甲、乙两车单独完成任务分别需要多少天?
(2)已知两车合运共需租金65000元,甲车每天的租金比乙车每天的租金多1500元,试问:租甲乙两车、单独租甲车、单独租乙车这三种租车方案中,哪一种租金最少?请说明理由.
(1)甲、乙两车单独完成任务分别需要多少天?
(2)已知两车合运共需租金65000元,甲车每天的租金比乙车每天的租金多1500元,试问:租甲乙两车、单独租甲车、单独租乙车这三种租车方案中,哪一种租金最少?请说明理由.
25.如图,在平面直角坐标系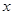 O
O 中,梯形AOBC的边OB在
中,梯形AOBC的边OB在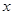 轴的正半轴上,AC//OB,BC⊥OB,过点A的双曲线
轴的正半轴上,AC//OB,BC⊥OB,过点A的双曲线 的一支在第一象限交梯形对角线OC于点D,交边BC于点
的一支在第一象限交梯形对角线OC于点D,交边BC于点
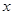 O
O 中,梯形AOBC的边OB在
中,梯形AOBC的边OB在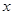 轴的正半轴上,AC//OB,BC⊥OB,过点A的双曲线
轴的正半轴上,AC//OB,BC⊥OB,过点A的双曲线 的一支在第一象限交梯形对角线OC于点D,交边BC于点
的一支在第一象限交梯形对角线OC于点D,交边BC于点A. (1)填空:双曲线的另一支在第 象限, 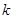 的取值范围是 ; 的取值范围是 ;(2)若点C的坐标为(2,2),当点E 在什么位置时,阴影部分面积S最小? (3)若  ,S△OAC="2" ,求双曲线的解析式. ,S△OAC="2" ,求双曲线的解析式. |
26.如图,在平面直角坐标系 O
O 中,矩形AOCD的顶点A的坐标是(0,4),现有两动点P、Q,点P从点O出发沿线段OC(不包括端点O,C)以每秒2个单位长度的速度,匀速向点C运动,点Q从点C出发沿线段CD(不包括端点C,D)以每秒1个单位长度的速度匀速向点D运动.点P,Q同时出发,同时停止,设运动时间为t秒,当t=2秒时PQ=
中,矩形AOCD的顶点A的坐标是(0,4),现有两动点P、Q,点P从点O出发沿线段OC(不包括端点O,C)以每秒2个单位长度的速度,匀速向点C运动,点Q从点C出发沿线段CD(不包括端点C,D)以每秒1个单位长度的速度匀速向点D运动.点P,Q同时出发,同时停止,设运动时间为t秒,当t=2秒时PQ= .
.

(1)求点D的坐标,并直接写出t的取值范围;
(2)连接AQ并延长交 轴于点E,把AE沿AD翻折交CD延长线于点F,连接EF,则△AEF的面积S是否随t的变化而变化?若变化,求出S与t的函数关系式;若不变化,求出S的值.
轴于点E,把AE沿AD翻折交CD延长线于点F,连接EF,则△AEF的面积S是否随t的变化而变化?若变化,求出S与t的函数关系式;若不变化,求出S的值.
(3)在(2)的条件下,t为何值时,四边形APQF是梯形?
 O
O 中,矩形AOCD的顶点A的坐标是(0,4),现有两动点P、Q,点P从点O出发沿线段OC(不包括端点O,C)以每秒2个单位长度的速度,匀速向点C运动,点Q从点C出发沿线段CD(不包括端点C,D)以每秒1个单位长度的速度匀速向点D运动.点P,Q同时出发,同时停止,设运动时间为t秒,当t=2秒时PQ=
中,矩形AOCD的顶点A的坐标是(0,4),现有两动点P、Q,点P从点O出发沿线段OC(不包括端点O,C)以每秒2个单位长度的速度,匀速向点C运动,点Q从点C出发沿线段CD(不包括端点C,D)以每秒1个单位长度的速度匀速向点D运动.点P,Q同时出发,同时停止,设运动时间为t秒,当t=2秒时PQ= .
.
(1)求点D的坐标,并直接写出t的取值范围;
(2)连接AQ并延长交
 轴于点E,把AE沿AD翻折交CD延长线于点F,连接EF,则△AEF的面积S是否随t的变化而变化?若变化,求出S与t的函数关系式;若不变化,求出S的值.
轴于点E,把AE沿AD翻折交CD延长线于点F,连接EF,则△AEF的面积S是否随t的变化而变化?若变化,求出S与t的函数关系式;若不变化,求出S的值.(3)在(2)的条件下,t为何值时,四边形APQF是梯形?
 搜索
搜索
 难度系数:0.94
难度系数:0.94  答案解析
答案解析
 有奖纠错
有奖纠错
