搜索
全一卷
难度系数：0.94 
答案解析
有奖纠错
1．若a与1互为相反数，则|a+1|等于（ ）
| A．﹣1 | B．0 | C．1 | D．2 |
2．如图是某几何体的三视图，该几何体是（）
| A．圆柱 | B．圆锥 | C．正三棱柱 | D．正三棱锥 |
3．某种细胞的直径是0.000067厘米，将0.000067用科学记数法表示为（ ）
| A．0.67×10-5 | B．67×10-6 | C．6.7×10-6 | D．6.7×10-5 |
4．在天水市汉字听写大赛中，10名学生得分情况如表
那么这10名学生所得分数的中位数和众数分别是（ ）
| 人数 | 3 | 4 | 2 | 1 |
| 分数 | 80 | 85 | 90 | 95 |
那么这10名学生所得分数的中位数和众数分别是（ ）
| A．85和82.5 | B．85.5和85 | C．85和85 | D．85.5和80 |
5．二次函数y=ax2+bx﹣1（a≠0）的图象经过点（1，1），则a+b+1的值是（ ）
| A．﹣3 | B．﹣1 | C．2 | D．3 |
6．一个圆柱的侧面展开图是两邻边长分别为6和8的矩形，则该圆柱的底面圆半径是（）
A． | B． | C．或 | D． 或 |
7．如图，将矩形纸带ABCD，沿EF折叠后，C、D两点分别落在C′、D′的位置，经测量得∠EFB=65°，则∠AED′的度数是（ ）
| A．65° | B．55° | C．50° | D．25° |
8．如图，在四边形ABCD中，∠BAD=∠ADC=90°，AB=AD=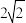
，CD=
，点P在四边形ABCD的边上．若点P到BD的距离为
，则点P的个数为（ ）
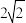，CD=
，点P在四边形ABCD的边上．若点P到BD的距离为
，则点P的个数为（ ）
| A．2 | B．3 | C．4 | D．5 |
9．如图，AB为半圆所在⊙O的直径，弦CD为定长且小于⊙O的半径（C点与A点不重合），CF⊥CD交AB于点F，DE⊥CD交AB于点E，G为半圆弧上的中点．当点C在
上运动时，设的长为x，CF+DE=y．则下列图象中，能表示y与x的函数关系的图象大致是（）
上运动时，设的长为x，CF+DE=y．则下列图象中，能表示y与x的函数关系的图象大致是（）
A． | B． | C． | D． |
10．定义运算：a⊗b=a（1﹣b）．下面给出了关于这种运算的几种结论：
①2⊗（﹣2）=6，
②a⊗b=b⊗a，
③若a+b=0，则（a⊗a）+（b⊗b）=2ab，
④若a⊗b=0，则a=0或b=1，
其中结论正确的序号是（）
①2⊗（﹣2）=6，
②a⊗b=b⊗a，
③若a+b=0，则（a⊗a）+（b⊗b）=2ab，
④若a⊗b=0，则a=0或b=1，
其中结论正确的序号是（）
| A．①④ | B．①③ | C．②③④ | D．①②④ |
11．相切两圆的半径分别是5和3，则该两圆的圆心距是_____ ．
12．不等式组
的所有整数解是_____ ．
的所有整数解是13．如图，边长为1的小正方形构成的网格中，半径为1的⊙O在格点上，则∠AED的正切值为_____ ．
14．一元二次方程x2+3﹣2
x=0的解是_____ ．
x=0的解是15．如图是一位同学设计的用手电筒来测量某古城墙高度的示意图．点P处放一水平的平面镜，光线从点A出发经平面镜反射后刚好到古城墙CD的顶端C处，已知AB⊥BD，CD⊥BD，测得AB=2米，BP=3米，PD=12米，那么该古城墙的高度CD是_____ 米．
16．如图，△ABC是正三角形，曲线CDEF叫做正三角形的渐开线，其中弧CD、弧DE、弧EF的圆心依次是A、B、C，如果AB=1，那么曲线CDEF的长是_____ ．
17．下列函数（其中n为常数，且n＞1）
①y=
（x＞0）；②y=（n﹣1）x；③y=
（x＞0）；④y=（1﹣n）x+1；⑤y=﹣x2+2nx（x＜0）中，y的值随x的值增大而增大的函数有_____ 个．
①y=
（x＞0）；②y=（n﹣1）x；③y=
（x＞0）；④y=（1﹣n）x+1；⑤y=﹣x2+2nx（x＜0）中，y的值随x的值增大而增大的函数有18．正方形OA1B1C1、A1A2B2C2、A2A3B3C3，按如图放置，其中点A1、A2、A3在x轴的正半轴上，点B1、B2、B3在直线
上，则点A3的坐标为_____________．
上，则点A3的坐标为_____________．
19．（9分）（2015•天水）计算：
（1）（π﹣3）0+
﹣2cos45°﹣
（2）若x+
=3，求
的值．
（1）（π﹣3）0+
﹣2cos45°﹣
（2）若x+
=3，求
的值．20．某地发生8.1级地震，震源深度20千米．救援队火速赶往灾区救援，探测出某建筑物废墟下方点C处有生命迹象．在废墟一侧某面上选两探测点A、B，AB相距2米，探测线与该面的夹角分别是30°和45°（如图）．试确定生命所在点C与探测面的距离．（参考数据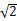
≈1.41，
≈1.73）
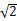≈1.41，
≈1.73）
21．（10分）（2015•天水）如图，在平面直角坐标系内，O为原点，点A的坐标为（﹣3，0），经过A、O两点作半径为
的⊙C，交y轴的负半轴于点B．
（1）求B点的坐标；
（2）过B点作⊙C的切线交x轴于点D，求直线BD的解析式．
的⊙C，交y轴的负半轴于点B．
（1）求B点的坐标；
（2）过B点作⊙C的切线交x轴于点D，求直线BD的解析式．
22．钓鱼岛是我国固有领土．某校七年级（15）班举行“爱国教育”为主题班会时，就有关钓鱼岛新闻的获取途径，对本班50名学生进行调查（要求每位同学，只选自己最认可的一项），并绘制如图所示的扇形统计图．
（1）该班学生选择“报刊”的有 人．在扇形统计图中，“其它”所在扇形区域的圆心角是 度．（直接填结果）
（2）如果该校七年级有1500名学生，利用样本估计选择“网站”的七年级学生约有 人．（直接填结果）
（3）如果七年级（15）班班委会就这5种获取途径中任选两种对全校学生进行调查，求恰好选用“网站”和“课堂”的概率．（用树状图或列表法分析解答）
（1）该班学生选择“报刊”的有 人．在扇形统计图中，“其它”所在扇形区域的圆心角是 度．（直接填结果）
（2）如果该校七年级有1500名学生，利用样本估计选择“网站”的七年级学生约有 人．（直接填结果）
（3）如果七年级（15）班班委会就这5种获取途径中任选两种对全校学生进行调查，求恰好选用“网站”和“课堂”的概率．（用树状图或列表法分析解答）
23．天水“伏羲文化节”商品交易会上，某商人将每件进价为8元的纪念品，按每件9元出售，每天可售出20件．他想采用提高售价的办法来增加利润，经实验，发现这种纪念品每件提价1元，每天的销售量会减少4件．
（1）写出每天所得的利润y（元）与售价x（元/件）之间的函数关系式．
（2）每件售价定为多少元，才能使一天所得的利润最大？最大利润是多少元？
（1）写出每天所得的利润y（元）与售价x（元/件）之间的函数关系式．
（2）每件售价定为多少元，才能使一天所得的利润最大？最大利润是多少元？
24．如图，点A（m，6）、B（n，1）在反比例函数图像上，AD⊥x轴于点D，BC⊥x轴于点C，DC=5．
（1）求m、n的值并写出该反比例函数的解析式．
（2）点E在线段CD上，S△ABE=10，求点E的坐标．
（1）求m、n的值并写出该反比例函数的解析式．
（2）点E在线段CD上，S△ABE=10，求点E的坐标．
25．（12分）（2015•天水）如图，AB是⊙O的直径，BC切⊙O于点B，OC平行于弦AD，过点D作DE⊥AB于点E，连结AC，与DE交于点P．求证：
（1）PE=PD；
（2）AC•PD=AP•BC．
（1）PE=PD；
（2）AC•PD=AP•BC．
26．在平面直角坐标系中，已知y=﹣
x2+bx+c（b、c为常数）的顶点为P，等腰直角三角形ABC的顶点A的坐标为（0，﹣1），点C的坐标为（4，3），直角顶点B在第四象限．
（1）如图，若抛物线经过A、B两点，求抛物线的解析式．
（2）平移（1）中的抛物线，使顶点P在直线AC上并沿AC方向滑动距离为
时，试证明：平移后的抛物线与直线AC交于x轴上的同一点．
（3）在（2）的情况下，若沿AC方向任意滑动时，设抛物线与直线AC的另一交点为Q，取BC的中点N，试探究NP+BQ是否存在最小值？若存在，求出该最小值；若不存在，请说明理由．
x2+bx+c（b、c为常数）的顶点为P，等腰直角三角形ABC的顶点A的坐标为（0，﹣1），点C的坐标为（4，3），直角顶点B在第四象限．（1）如图，若抛物线经过A、B两点，求抛物线的解析式．
（2）平移（1）中的抛物线，使顶点P在直线AC上并沿AC方向滑动距离为
时，试证明：平移后的抛物线与直线AC交于x轴上的同一点．（3）在（2）的情况下，若沿AC方向任意滑动时，设抛物线与直线AC的另一交点为Q，取BC的中点N，试探究NP+BQ是否存在最小值？若存在，求出该最小值；若不存在，请说明理由．
