搜索
全一卷
难度系数：0.65 
答案解析
有奖纠错
1．计算-32的值是
| A．9 | B．-9 | C．6 | D．-6 |
2．太阳的半径约为696000km，把696000这个数用科学记数法表示为
| A．6.96×103 | B．69.6×105 | C．6.96×105 | D．6.96×106 |
3．如图，
，
，则
等于（ ）
，，则等于（ ）A． | B． | C． | D． |
4．下列计算正确的是
A． | B． | C． | D． |
5．为了考察某种小麦的长势，从中抽取了10株麦苗，测得苗高（单位：cm）为：16， 9， 14， 11， 12， 10， 16， 8， 17， 19则这组数据的中位数和极差分别是（ ）
| A．13，16 | B．14，11 | C．12，11 | D．13，11 |
6．下列说法正确的是
| A．平分弦的直径垂直于弦 | B．半圆（或直径）所对的圆周角是直角 |
| C．相等的圆心角所对的弧相等 | D．若两个圆有公共点，则这两个圆相交 |
7．使不等式
与
同时成立的x的整数值是（ ）
与同时成立的x的整数值是（ ）| A．3，4 | B．4，5 | C．3，4，5 | D．不存在 |
8．式子
的值是（ ）
的值是（ ）A． | B．0 | C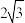． | D．0 |
9．在平面直角坐标系中，已知点E（﹣4，2），F（﹣2，﹣2），以原点O为位似中心，相似比为2∶1，把△EFO缩小，则点E的对应点E′的坐标是
| A．（﹣2，1） | B．（﹣8，4） | C．（﹣8，4）或（8，﹣4） | D．（﹣2，1）或（2，﹣1） |
10．如图，由8个大小相同的正方体组成的几何体的主视图和俯视图，则这个几何体的左视图是（ ）
A． | B． | C． | D． |
11．如图，函数
与函数
的图象相交于A，B两点，过A，B两点分别作y轴的垂线，垂足分别为点C，D．则四边形ACBD的面积为( )
与函数
的图象相交于A，B两点，过A，B两点分别作y轴的垂线，垂足分别为点C，D．则四边形ACBD的面积为( )
| A．2 | B．4 | C．6 | D．8 |
12．如图，在△ABC中，AB=AC=a，BC=b（a＞b）．在△ABC内依次作∠CBD=∠A，∠DCE=∠CBD，∠EDF=∠DCE．则EF等于（）
A． | B． | C． | D． |
13．分解因式：
=_____ ．
=14．在5瓶饮料中，有2瓶已过了保质期，从这5瓶饮料中任取1瓶，取到已过保质期饮料的概率为_____ （结果用分数表示）．
15．如图，两建筑物的水平距离BC为18m，从A点测得D点的俯角α为300，测得C点的俯角β为600．则建筑物CD的高度为_____ m（结果不作近似计算）．
16．用半径为10cm，圆心角为216°的扇形做成一个圆锥的侧面，则这个圆锥的高为_____ cm．
17．如图，古希腊人常用小石子在沙滩上摆成各种形状来研究数．例如：称图中的数1，5，12，22…为五边形数，则第6个五边形数是_____ ．
18．如图，一个装有进水管和出水管的容器，从某时刻开始的4分钟内只进水不出水，在随后的8分钟内既进水又出水，接着关闭进水管直到容器内的水放完．假设每分钟的进水量和出水量是两个常数，容器内的水量y（单位：升）与时间x（单位：分）之间的部分关系．那么，从关闭进水管起_____ 分钟该容器内的水恰好放完．
19．先化简，再求值：
，其中
．
，其中
．20．如图，已知△ABC和点O．
（1）把△ABC绕点O顺时针旋转90
得到△A1B1C1，在网格中画出△A1B1C1；
（2）用直尺和圆规作△ABC的边AB，AC的垂直平分线，并标出两条垂直平分线的交点P（要求保留作图痕迹，不写作法）；指出点P是△ABC的内心，外心，还是重心？
（1）把△ABC绕点O顺时针旋转90
得到△A1B1C1，在网格中画出△A1B1C1；（2）用直尺和圆规作△ABC的边AB，AC的垂直平分线，并标出两条垂直平分线的交点P（要求保留作图痕迹，不写作法）；指出点P是△ABC的内心，外心，还是重心？
21．如图，暑假快要到了，某市准备组织同学们分别到A，B，C，D四个地方进行夏令营活动，前往四个地方的人数．
（1）去B地参加夏令营活动人数占总人数的40%，根据统计图求去B地的人数？
（2）若一对姐弟中只能有一人参加夏令营，姐弟俩提议让父亲决定．父亲说：现有4张卡片上分别写有1，2，3，4四个整数，先让姐姐随机地抽取一张后放回，再由弟弟随机地抽取一张．若抽取的两张卡片上的数字之和是5的倍数则姐姐参加，若抽取的两张卡片上的数字之和是3的倍数则弟弟参加．用列表法或树形图分析这种方法对姐弟俩是否公平？
（1）去B地参加夏令营活动人数占总人数的40%，根据统计图求去B地的人数？
（2）若一对姐弟中只能有一人参加夏令营，姐弟俩提议让父亲决定．父亲说：现有4张卡片上分别写有1，2，3，4四个整数，先让姐姐随机地抽取一张后放回，再由弟弟随机地抽取一张．若抽取的两张卡片上的数字之和是5的倍数则姐姐参加，若抽取的两张卡片上的数字之和是3的倍数则弟弟参加．用列表法或树形图分析这种方法对姐弟俩是否公平？
22．在“母亲节”前夕，我市某校学生积极参与“关爱贫困母亲”的活动，他们购进一批单价为20元的“孝文化衫”在课余时间进行义卖，并将所得利润捐给贫困母亲．经试验发现，若每件按24元的价格销售时，每天能卖出36件；若每件按29元的价格销售时，每天能卖出21件．假定每天销售件数y（件）与销售价格x（元/件）满足一个以x为自变量的一次函数．
（1）求y与x满足的函数关系式（不要求写出x的取值范围）；
（2）在不积压且不考虑其他因素的情况下，销售价格定为多少元时，才能使每天获得的利润P最大？
（1）求y与x满足的函数关系式（不要求写出x的取值范围）；
（2）在不积压且不考虑其他因素的情况下，销售价格定为多少元时，才能使每天获得的利润P最大？
23．如图，△ABC内接于⊙O，∠B=600，CD是⊙O的直径，点P是CD延长线上的一点，且AP=AC，
（1）求证：PA是⊙O的切线；
（2）若PD=
，求⊙O的直径．
（1）求证：PA是⊙O的切线；
（2）若PD=
，求⊙O的直径．24．已知关于x的一元二次方程
有两个实数根x1，x2．
（1）求实数k的取值范围；
（2）是否存在实数k使得
成立？若存在，请求出k的值；若不存在，请说明理由．
有两个实数根x1，x2．（1）求实数k的取值范围；
（2）是否存在实数k使得
成立？若存在，请求出k的值；若不存在，请说明理由．25．如图1，已知正方形ABCD的边长为1，点E在边BC上，若∠AEF=900，且EF交正方形外角的平分线CF于点F
（1）图1中若点E是边BC的中点，我们可以构造两个三角形全等来证明AE=EF，请叙述你的一个构造方案，并指出是哪两个三角形全等（不要求证明）；
（2）如图2，若点E在线段BC上滑动（不与点B，C重合）．
①AE=EF是否总成立？请给出证明；
②在如图2的直角坐标系中，当点E滑动到某处时，点F恰好落在抛物线
上，求此时点F的坐标．
（1）图1中若点E是边BC的中点，我们可以构造两个三角形全等来证明AE=EF，请叙述你的一个构造方案，并指出是哪两个三角形全等（不要求证明）；
（2）如图2，若点E在线段BC上滑动（不与点B，C重合）．
①AE=EF是否总成立？请给出证明；
②在如图2的直角坐标系中，当点E滑动到某处时，点F恰好落在抛物线
上，求此时点F的坐标．