搜索
全一卷
难度系数：0.65 
答案解析
有奖纠错
1．（2011•广元）下列计算正确的是（）
| A．（a2）5=a10 | B．a2+a5=a7 |
C． =﹣2 | D．6 •2=12 |
2．（2011•广元）反比例函数y=
（a是常数）的图象分布在（）
（a是常数）的图象分布在（）| A．第一、二象限 | B．第一、三象限 |
| C．第二、四象限 | D．第三、四象限 |
3．（2011•广元）若数据8、4、x、2的平均数是4，则这组数据的众数和中位数分别是（）
| A．2和2 | B．2和4 |
| C．2和3 | D．3和2 |
4．如图，边长为1的正方形
绕点A逆时针旋转
后得到正方形
，边
与
交于点O，则四边形
的周长是（ ）
绕点A逆时针旋转后得到正方形，边与交于点O，则四边形的周长是（ ） A． | B． |
C．  | D．3 |
5．（2011•广元）在《国家中长期教育改革和发展规划纲要》中指出，“加大教育投入，提高国家财政性教育经费支出占国内生产总值比例，2012年达到4%．”如果2012年我国国内生产总值为445000亿元，那么2012年国家财政性教育经费支出应为（结果用科学记数法表示）（）
| A．178×102亿元 | B．1.78×104亿元 |
| C．1.78×105亿元 | D．4.45×105亿元 |
6．（2011?广元）下列几何体中，其各自的主视图、左视图、俯视图中有两个相同，而另一个不同的是（）
| A．①② | B．②③ |
| C．②④ | D．③④ |
7．我省在家电下乡活动中，冰箱、彩电、洗衣机和空调这四种家电的销售比例为
，其中空调已销售了15万台．根据此信息绘制的扇形统计图中，已销售冰箱部分所对应的圆心角的度数和四种家电销售的总台数分别为（ ）
，其中空调已销售了15万台．根据此信息绘制的扇形统计图中，已销售冰箱部分所对应的圆心角的度数和四种家电销售的总台数分别为（ ）| A．150°和180万台 | B．150°和75万台 |
| C．180°和180万台 | D．180°和75万台 |
8．若用圆心角为120°，半径为9的扇形围成一个圆锥侧面（接缝忽略不计），则这个圆锥的底面直径是（ ）
| A．3 | B．6 |
| C．9 | D．12 |
9．（2011•广元）函数
的自变量x的取值范围在数轴上表示为（）
的自变量x的取值范围在数轴上表示为（）A． | B． |
C． | D． |
10．在平面直角坐标系中，如果抛物线y=3x2不动，而把x轴、y轴分别向上、向右平移3个单位，那么在新坐标系中此抛物线的解析式是（ ）
| A．y=3（x﹣3）2+3 | B．y=3（x﹣3）2﹣3 |
| C．y=3（x+3）2+3 | D．y=3（x+3）2﹣3 |
11．在﹣1、0、1、2这四个数中，既不是正数也不是负数的是___________ ．
12．甲、乙两人5次射击命中的环数如下：
则这两人5次射击命中的环数的平均数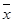
甲=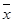乙=8，方差S2甲____ S2乙（填“＞”、“=”或“＜”）．
则这两人5次射击命中的环数的平均数
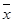甲=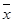乙=8，方差S2甲13．已知⊙O1和⊙O2的半径分别是一元二次方程
的两根，且O1O2=1，则⊙O1和⊙O2的位置关系是___________ ．
的两根，且O1O2=1，则⊙O1和⊙O2的位置关系是14．（2011•广元）如图，M为矩形纸片ABCD的边AD的中点，将纸片沿BM、CM折叠，使点A落在A1处，点D落在D1处．若∠A1MD1=40°，则∠BMC的度数为___________ ．
15．已知一组数为：1，
，
，
，
…按此规律用代数式表示第n个数为___________ ．
，
，
，
…按此规律用代数式表示第n个数为16．（2011?广元）计算：
．
．17．先化简
÷
，再选取一个既使原式有意义，又是你喜欢的数代入求值．
÷
，再选取一个既使原式有意义，又是你喜欢的数代入求值．18．如图，在△ABC和△ACD中，CB=CD，设点E是CB的中点，点F是CD的中点．
（1）请你在图中作出点E和点F（尺规作图，保留作图痕迹，不写作法与证明）；
（2）连接AE、AF，若∠ACB=∠ACD，请问△ACE≌△ACF吗？请说明理由．
（1）请你在图中作出点E和点F（尺规作图，保留作图痕迹，不写作法与证明）；
（2）连接AE、AF，若∠ACB=∠ACD，请问△ACE≌△ACF吗？请说明理由．
19．张师傅驾车运送草莓到某地出售，汽车出发前油箱有油50升，行驶若干小时后，途中在加油站加油若干升，油箱中剩余油量
(升)与行驶时间
(小时)之间的关系如图所示．
请根据图象回答下列问题：
（1）汽车行驶 小时后加油，中途加油 升；
（2）求加油前油箱剩余油量与行驶时间的函数关系式；
（3）已知加油前、后汽车都以70千米/小时匀速行驶，如果加油站距目的地210千米，要到达目的地，问油箱中的油是否够用？请说明理由．
(升)与行驶时间
(小时)之间的关系如图所示．
请根据图象回答下列问题：
（1）汽车行驶 小时后加油，中途加油 升；
（2）求加油前油箱剩余油量
与行驶时间的函数关系式；（3）已知加油前、后汽车都以70千米/小时匀速行驶，如果加油站距目的地210千米，要到达目的地，问油箱中的油是否够用？请说明理由．
20．有甲、乙两个黑布袋，甲布袋中有四个除标号外完全相同的小球，小球上分别标有数字0、1、2、3；乙布袋中有三个除标号外完全相同的小球，小球上分别标有数字0、1、2．王红先从甲布袋中随机取出一个小球，用m表示取出的球上标有的数字，再从乙布袋中随机取出一个小球，用n表示取出的球上标有的数字．
（1）若用（m，n）表示王红取球时m与n的对应值，请画出树状图或列表写出（m，n）的所有取值情况；
（2）求出点（m，n）落在函数y=
的图象上的概率，并写出这些点的坐标．
（1）若用（m，n）表示王红取球时m与n的对应值，请画出树状图或列表写出（m，n）的所有取值情况；
（2）求出点（m，n）落在函数y=
的图象上的概率，并写出这些点的坐标．21．如图，在直角梯形ABCD中，AD∥BC，BC⊥CD，∠B=60°，BC=2AD，E、F分别为AB、BC的中点．
（1）求证：四边形AFCD是矩形；
（2）求证：DE⊥EF.
（1）求证：四边形AFCD是矩形；
（2）求证：DE⊥EF.
22．某童装店到厂家选购A、B两种服装．若购进A种服装12件、B种服装8件，需要资金1880元；若购进A种服装9件、B种服装10件，需要资金1810元．
（1）求A、B两种服装的进价分别为多少元？
（2）销售一件A服装可获利18元，销售一件B服装可获利30元．根据市场需求，服装店决定：购进A种服装的数量要比购进B种服装的数量的2倍还多4件，且A种服装购进数量不超过28件，并使这批服装全部销售完毕后的总获利不少于699元．设购进B种服装x件，那么:
①请写出A、B两种服装全部销售完毕后的总获利y元与x件之间的函数关系式；
②请问该服装店有几种满足条件的进货方案？哪种方案获利最多？
（1）求A、B两种服装的进价分别为多少元？
（2）销售一件A服装可获利18元，销售一件B服装可获利30元．根据市场需求，服装店决定：购进A种服装的数量要比购进B种服装的数量的2倍还多4件，且A种服装购进数量不超过28件，并使这批服装全部销售完毕后的总获利不少于699元．设购进B种服装x件，那么:
①请写出A、B两种服装全部销售完毕后的总获利y元与x件之间的函数关系式；
②请问该服装店有几种满足条件的进货方案？哪种方案获利最多？
23．如图，AB是⊙O的直径，BC切⊙O于点B，连接CO并延长交⊙O于点D、E，连接AD并延长交BC于点F．
（1）试判断∠CBD与∠CEB是否相等，并证明你的结论；
（2）求证：
；
（3）若BC=
AB，求tan∠CDF的值．
（1）试判断∠CBD与∠CEB是否相等，并证明你的结论；
（2）求证：
；（3）若BC=
AB，求tan∠CDF的值．
24．如图，抛物线y=ax2+2ax+c（a≠0）与y轴交于点C（0，4），与x轴交于点A（﹣4，0）和
| A． （1）求该抛物线的解析式； （2）点Q是线段AB上的动点，过点Q作QE∥AC，交BC于点E，连接CQ．当△CEQ的面积最大时，求点Q的坐标； （3）平行于x轴的动直线l与该抛物线交于点P，与直线AC交于点F，点D的坐标为（﹣2，0）．问是否有直线l，使△ODF是等腰三角形？若存在，请求出点F的坐标；若不存在，请说明理由． |
