搜索
全一卷
难度系数：0.85 
答案解析
有奖纠错
1．下列计算正确的是
| A．a2+a3=a5 | B．a6÷a2=a3 | C．a2•a3=a6 | D．（a4）3=a12 |
2．钓鱼岛是中国的固有领土，位于中国东海，面积约4400000平方米，数据4400000用科学记数法表示为（ ）
| A．44×105 | B．0.44×105 | C．4.4×106 | D．4.4×105 |
3．如图，是一个正方体的表面展开图，则原正方体中“梦”字所在的面相对的面上标的字是（ ）
| A．大 | B．伟 |
| C．国 | D．的 |
4．体育课上，某班两名同学分别进行5次短跑训练，要判断哪一名同学的成绩比较稳定，通常需要比较这两名学生成绩的（ ）
| A．平均数 | B．频数分布 | C．中位数 | D．方差 |
5．在物理实验课上，小明用弹簧称将铁块A悬于盛有水的水槽中，然后匀速向上提起，直至铁块完全露出水面一定高度，则下图能反映弹簧称的读数y(单位N)与铁块被提起的高度x(单位cm)之间的函数关系的大致图象是（ ）
A． | B． | C． | D． |
6．如图，在梯形ABCD中，AD∥BC，点E、F分别是AB、CD的中点且EF=6，则AD+BC的值是( )
| A．9 | B．10.5 | C．12 | D．15 |
7．下列命题是真命题的是
| A．无限小数是无理数 |
| B．相反数等于它本身的数是0和1 |
| C．对角线互相平分且相等的四边形是矩形 |
| D．等边三角形既是中心对称图形，又是轴对称图形 |
8．如图，已知⊙O是△ABD的外接圆，AB是⊙O的直径，CD是⊙O的弦，∠ABD=58°，则∠BCD等于（ ）
| A．116° | B．32° | C．58° | D．64° |
9．如图,菱形ABCD的两条对角线相交于O,若AC=6,BD=4,则菱形ABCD的周长是( )
| A．24 | B．16 | C． | D． |
10．已知二次函数
（a≠0）的图象如图所示，则下列结论中正确的是
（a≠0）的图象如图所示，则下列结论中正确的是
| A．ac＞0 |
| B．当x＞1时，y随x的增大而减小 |
| C．b﹣2a=0 |
D．x=3是关于x的方程 （a≠0）的一个根 |
11．分解因式：2m2-8=_______________．
12．若一个多边形外角和与内角和相等，则这个多边形是_____ ．
13．函数
中，自变量x的取值范围是 ．
中，自变量x的取值范围是 ．14．如图，已知点B、C、F、E在同一直线上，∠1=∠2，BC=EF，要使△ABC≌△DEF，还需添加一个条件，这个条件可以是 ．（只需写出一个）
15．在－1、3、－2这三个数中，任选两个数的积作为k的值，使反比例函数
的图象在第一、三象限的概率是 ．
的图象在第一、三象限的概率是 ．16．底面半径为1，母线长为2的圆锥的侧面积等于_____ ．
17．方程
的两个根是等腰三角形的底和腰，则这个等腰三角形的周长为_____ ．
的两个根是等腰三角形的底和腰，则这个等腰三角形的周长为18．如图，小明在打网球时，使球恰好能打过网，而且落在离网4米的位置上，则球拍击球的高度h为_____ ．
19．若直角三角形的两直角边长为a、b，且满足
，则该直角三角形的斜边长为_____ ．
，则该直角三角形的斜边长为20．观察下面的单项式：a，－2a2，4a3，－8a4，…根据你发现的规律，第8个式子是_____ ．
21．计算：
．
．22．解不等式：
，并把解集表示在数轴上．
，并把解集表示在数轴上．23．先化简
，然后a在﹣1、1、2三个数中任选一个合适的数代入求值．
，然后a在﹣1、1、2三个数中任选一个合适的数代入求值．24．△ABC在平面直角坐标系xOy中的位置如图所示．
（1）作△ABC关于点C成中心对称的△A1B1C1，
（2）将△A1B1C1向右平移4个单位，作出平移后的△A2B2C2，
（3）在x轴上求作一点P，使PA1＋PC2的值最小，并写出点P的坐标（不写解答过程，直接写出结果）
（1）作△ABC关于点C成中心对称的△A1B1C1，
（2）将△A1B1C1向右平移4个单位，作出平移后的△A2B2C2，
（3）在x轴上求作一点P，使PA1＋PC2的值最小，并写出点P的坐标（不写解答过程，直接写出结果）
25．为了把巴城建成省级文明城市，特在每个红绿灯处设置了文明监督岗，文明劝导员老张某天在市中心的一十字路口，对闯红灯的人数进行统计．根据上午7：00～12：00中各时间段（以1小时为一个时间段），对闯红灯的人数制作了如图所示的扇形统计图和条形统计图，但均不完整．请你根据统计图解答下列问题：
（1）问这一天上午7：00～12：00这一时间段共有多少人闯红灯？
（2）请你把条形统计图补充完整，并求出扇形统计图中9～10点，10～11点所对应的圆心角的度数．
（3）求这一天上午7：00～12：00这一时间段中，各时间段闯红灯的人数的众数和中位数．
（1）问这一天上午7：00～12：00这一时间段共有多少人闯红灯？
（2）请你把条形统计图补充完整，并求出扇形统计图中9～10点，10～11点所对应的圆心角的度数．
（3）求这一天上午7：00～12：00这一时间段中，各时间段闯红灯的人数的众数和中位数．
26．若⊙O1和⊙O2的圆心距为4，两圆半径分别为r1、r2，且r1、r2是方程组
的解，求r1、r2的值，并判断两圆的位置关系．
的解，求r1、r2的值，并判断两圆的位置关系．27．某商场今年2月份的营业额为
万元，3月份的营业额比2月份增加
，
月份的营业额达到
万元．求3月份到5月份营业额的平均月增长率．
万元，3月份的营业额比2月份增加
，
月份的营业额达到
万元．求3月份到5月份营业额的平均月增长率．28．2013年4月20日，四川雅安发生里氏7.0级地震，救援队救援时，利用生命探测仪在某建筑物废墟下方探测到点C处有生命迹象，已知废墟一侧地面上两探测点A、B相距4米，探测线与地面的夹角分别为300和600，如图所示，试确定生命所在点C的深度（结果精确到0.1米，参考数据
≈1.41，
≈1.73）
≈1.41，
≈1.73）
29．如图，在平行四边形ABCD中，过点A作AE⊥BC，垂足为E，连接DE，F为线段DE上一点，且∠AFE=∠B
（1）求证：△ADF∽△DEC；
（2）若AB=8，AD=6
，AF=4，求AE的长．
（1）求证：△ADF∽△DEC；
（2）若AB=8，AD=6
，AF=4，求AE的长．30．如图，在平面直角坐标系xOy中，一次函数y=kx+b（k≠0）的图象与反比例函数
的图象交于一、三象限内的A、B两点，直线AB与x轴交于点C，点B的坐标为（﹣6，n），线段OA=5，E为x轴正半轴上一点，且tan∠AOE=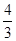
（1）求反比例函数的解析式；
（2）求△AOB的面积．
的图象交于一、三象限内的A、B两点，直线AB与x轴交于点C，点B的坐标为（﹣6，n），线段OA=5，E为x轴正半轴上一点，且tan∠AOE=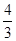
（1）求反比例函数的解析式；
（2）求△AOB的面积．
31．如图，在平面直角坐标系中，坐标原点为O，A点坐标为（4，0），B点坐标为（﹣1，0），以AB的中点P为圆心，AB为直径作⊙P的正半轴交于点C．
（1）求经过A、B、C三点的抛物线所对应的函数解析式；
（2）设M为（1）中抛物线的顶点，求直线MC对应的函数解析式；
（3）试说明直线MC与⊙P的位置关系，并证明你的结论．
（1）求经过A、B、C三点的抛物线所对应的函数解析式；
（2）设M为（1）中抛物线的顶点，求直线MC对应的函数解析式；
（3）试说明直线MC与⊙P的位置关系，并证明你的结论．
