搜索
全一卷
难度系数：0.94 
答案解析
有奖纠错
1．﹣2的绝对值等于（ ）
| A．2 | B．﹣2 | C． | D．±2 |
2．计算2a－a，正确的结果是（）
| A．－2a3 | B．1 | C．2 | D．a |
3．要使分式
有意义，x的取值范围满足（ ）
有意义，x的取值范围满足（ ）| A．x=0 | B．x≠0 | C．x＞0 | D．x＜0 |
4．数据5，7，8，8，9的众数是（）
| A．5 | B．7 | C．8 | D．9、 |
5．如图，在Rt△ABC中，∠ACB=90°，AB=10，CD是AB边上的中线，则CD的长是（ ）
| A．20 | B．10 | C．5 | D． |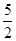
6．如图是七年级（1）班参加课外兴趣小组人数的扇形统计图，则表示唱歌兴趣小组人数的扇形的圆心角度数是（ ）
| A．36° | B．72° | C．108° | D．180° |
7．下列四个水平放置的几何体中，三视图如图所示的是【 】
A． | B． | C． | D． |
8．△ABC中的三条中位线围成的三角形周长是15cm，则△ABC的周长为( )
| A．60cm | B．45cm | C．30cm | D． cm |
9．如图，△ABC是⊙O的内接三角形，AC是⊙O的直径，∠C=50°，∠ABC的平分线BD交⊙O于点D，则∠BAD的度数是（ ）
| A．45° | B．85° | C．90° | D．95° |
10．如图，已知点A（4，0），O为坐标原点，P是线段OA上任意一点（不含端点O，A），过P、O两点的二次函数y1和过P、A两点的二次函数y2的图象开口均向下，它们的顶点分别为B、C，射线OB与AC相交于点D．当OD=AD=3时，这两个二次函数的最大值之和等于（）
A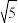． | B． | C．3 | D．4 |
11．当x=1时，代数式x+2的值是________ ．
12．因式分解：x2－36= _________ ．
13．甲、乙两名射击运动员在一次训练中，每人各打10发子弹，根据命中环数求得方差分别是
，则_______ 运动员的成绩比较稳定．
，则14．如图，在△ABC中，D、E分别是AB、AC上的点，点F在BC的延长线上，DE∥BC，∠A=46°，∠1=52°，则∠2=___________ 度．
15．一次函数y=kx+b（k，b为常数，且k≠0）的图象如图所示，根据图象信息可求得关于x的方程kx+b=0的解为________ ．
16．如图，将正
ABC分割成m个边长为1的小正三角形和一个黑色菱形，这个黑色菱形可分割成n个边长为1的小三角形，若
，则ABC的边长是_______ ．
ABC分割成m个边长为1的小正三角形和一个黑色菱形，这个黑色菱形可分割成n个边长为1的小三角形，若
，则ABC的边长是
17．计算：
．
．18．解方程组 
19．如图，已知反比例函数
（k≠0）的图象经过点（－2，8）．
（1）求这个反比例函数的解析式；
（2）若（2，y1），（4，y2）是这个反比例函数图象上的两个点，请比较y1、y2的大小，并说明理由．
（k≠0）的图象经过点（－2，8）．（1）求这个反比例函数的解析式；
（2）若（2，y1），（4，y2）是这个反比例函数图象上的两个点，请比较y1、y2的大小，并说明理由．
20．已知：如图，在平行四边形ABCD中，点F在AB的延长线上，且BF=AB，连接FD，交BC于点E．
(1)说明△DCE≌△FBE的理由；
(2)若EC=3，求AD的长．
(1)说明△DCE≌△FBE的理由；
(2)若EC=3，求AD的长．
21．某市开展了“雷锋精神你我传承，关爱老人从我做起”的主题活动，随机调查了本市部分老人与子女同住情况，根据收集到的数据，绘制成如下统计图表（不完整）
老人与子女同住情况百分比统计表
根据统计图表中的信息，解答下列问题：
（1）求本次调查的老人的总数及a、b的值；
（2）将条形统计图补充完整；（画在答卷相对应的图上）
（3）若该市共有老人约15万人，请估计该市与子女“同住”的老人总数．
老人与子女同住情况百分比统计表
| 老人与子女 同住情况 | 同住 | 不同住 （子女在本市） | 不同住 （子女在市外） | 其他 |
| | a | 50% | b | 5% |
根据统计图表中的信息，解答下列问题：
（1）求本次调查的老人的总数及a、b的值；
（2）将条形统计图补充完整；（画在答卷相对应的图上）
（3）若该市共有老人约15万人，请估计该市与子女“同住”的老人总数．
22．已知，如图，在梯形ABCD中，AD∥BC，DA=DC，以点D为圆心，DA长为半径的⊙D与AB相切于A，与BC交于点F，过点D作DE⊥BC，垂足为
| A． （1）求证：四边形ABED为矩形； （2）若AB=4，  ，求CF的长． |
23．为进一步建设秀美、宜居的生态环境，某村欲购买甲、乙、丙三种树美化村庄，已知甲、乙丙三种树的价格之比为2：2：3，甲种树每棵200元，现计划用210000元资金，购买这三种树共1000棵．
（1）求乙、丙两种树每棵各多少元？
（2）若购买甲种树的棵树是乙种树的2倍，恰好用完计划资金，求这三种树各能购买多少棵？
（3）若又增加了10120元的购树款，在购买总棵树不变的前提下，求丙种树最多可以购买多少棵？
（1）求乙、丙两种树每棵各多少元？
（2）若购买甲种树的棵树是乙种树的2倍，恰好用完计划资金，求这三种树各能购买多少棵？
（3）若又增加了10120元的购树款，在购买总棵树不变的前提下，求丙种树最多可以购买多少棵？
24．如图1，已知菱形ABCD的边长为
，点A在x轴负半轴上，点B在坐标原点．点D的坐标为（- 
，3），抛物线y=ax2+b（a≠0）经过AB、CD两边的中点．
（1）求这条抛物线的函数解析式；
（2）将菱形ABCD以每秒1个单位长度的速度沿x轴正方向匀速平移（如图2），过点B作BE⊥CD于点E，交抛物线于点F，连接DF、AF．设菱形ABCD平移的时间为t秒（0＜t＜ 3 ）
①是否存在这样的t，使△ADF与△DEF相似？若存在，求出t的值；若不存在，请说明理由；
②连接FC，以点F为旋转中心，将△FEC按顺时针方向旋转180°，得△FE′C′，当△FE′C′落在x轴与抛物线在x轴上方的部分围成的图形中（包括边界）时，求t的取值范围．（写出答案即可）
，点A在x轴负半轴上，点B在坐标原点．点D的坐标为（- 
，3），抛物线y=ax2+b（a≠0）经过AB、CD两边的中点．（1）求这条抛物线的函数解析式；
（2）将菱形ABCD以每秒1个单位长度的速度沿x轴正方向匀速平移（如图2），过点B作BE⊥CD于点E，交抛物线于点F，连接DF、AF．设菱形ABCD平移的时间为t秒（0＜t＜ 3 ）
①是否存在这样的t，使△ADF与△DEF相似？若存在，求出t的值；若不存在，请说明理由；
②连接FC，以点F为旋转中心，将△FEC按顺时针方向旋转180°，得△FE′C′，当△FE′C′落在x轴与抛物线在x轴上方的部分围成的图形中（包括边界）时，求t的取值范围．（写出答案即可）
