搜索
全一卷
难度系数：0.94 
答案解析
有奖纠错
1．-2的绝对值是（ ）
| A．2 | B． | C． | D． |
2．中国人口众多，地大物博，仅领水面积就约为370 000km2，将“370 000”这个数用科学记数法表示为（）．
A． | B． | C． | D． |
3．在数轴上表示不等式2（1﹣x）＜4的解集，正确的是（ ）
A． | B． |
C． | D． |
4．如图，是一台自动测温仪记录的图象，它反映了我市冬季某天气温T随时间t变化而变化的关系，观察图象得到下列信息，其中错误的是（ ）
| A．凌晨4时气温最低为－3℃ |
| B．14时气温最高为8℃ |
| C．从0时至14时，气温随时间增长而上升 |
| D．从14时至24时，气温随时间增长而下降 |
5．下列运算中正确的是（）
A． | B． |
C． | D． |
6．如图，将一块含有30°角的直角三角板的两个顶点放在矩形直尺的一组对边上．如果∠2=60°，那么∠1的度数为（ ）
| A．60° | B．50° | C．40° | D．30° |
7．如图，在△ABC中，∠B=30°，BC的垂直平分线交AB于点E，垂足为D，CE平分∠ACB，若BE=2，则AE的长为（ ）
A． | B．1 | C． | D．2 |
8．下列说法中正确的是（ ）
| A．“任意画出一个等边三角形，它是轴对称图形”是随机事件 |
| B．“任意画出一个平行四边形，它是中心对称图形”是必然事件 |
| C．“概率为0.0001的事件”是不可能事件 |
| D．任意掷一枚质地均匀的硬币10次，正面向上的一定是5次 |
9．点O是△ABC的外心，若∠BOC=80°，则∠BAC的度数为（ ）
| A．40° | B．100° | C．40°或140° | D．40°或100° |
10．由若干个相同的小正方体组合而成的一个几何体的三视图如图所示，则组成这个几何体的小正方体的个数是（ ）
| A．4 | B．5 | C．6 | D．9 |
11．二次函数y=ax2+bx+c的图象在平面直角坐标系中的位置如图所示，则一次函数y=ax+b与反比例函数y=
在同一平面直角
坐标系中的图象可能是（ ）
在同一平面直角
坐标系中的图象可能是（ ）
A． | B． | C． | D． |
12．如图，矩形纸片ABCD中，AB＝4，BC＝8，将纸片沿EF折叠，使点C与点A重合，则下列结论错误的是（ ）
| A．AF＝AE | B．△ABE≌△AGF | C．EF＝ | D．AF＝EF |
13．计算：
_____ ．
14．分式方程
的解是 ．
的解是 ．15．若一组数据1，2，x，4的众数是1，则这组数据的方差为_____ ．
16．如图，P为⊙O外一点，PA，PB是⊙O的切线，A，B为切点，PA＝
，∠P＝60°，则图中阴影部分的面积为____ ．
，∠P＝60°，则图中阴影部分的面积为
17．在▱ABCD中，AD=BD，BE是AD边上的高，∠EBD=20°，则∠A的度数为_________ ．
18．先化简，再求值：
，其中
，
．
，其中
，
．19．如图，已知反比例函数
的图象与一次函数
的图象相交于点A（1，4）和点B（n，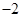
）．
（1）求反比例函数和一次函数的解析式；
（2）当一次函数的值小于反比例函数的值时，直接写出x的取值范围．
的图象与一次函数
的图象相交于点A（1，4）和点B（n，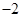
）．
（1）求反比例函数和一次函数的解析式；
（2）当一次函数的值小于反比例函数的值时，直接写出x的取值范围．
20．为配合全市“禁止焚烧秸秆”工作，某学校举行了“禁止焚烧秸秆，保护环境，从我做起”为主题的演讲比赛. 赛后组委会整理参赛同学的成绩，并制作了如下不完整的频数分布表（图1）和频数分布直方图(图2).
请根据图表提供的信息，解答下列问题：
(1)表中的a＝ ，b＝ (2)请补全频数分布直方图；
(3)若用扇形统计图来描述成绩分布情况，则分数段70≤x＜80对应的圆心角的度数是 ；
(4)竞赛成绩不低于90分的4名同学中正好有2名男同学，2名女同学.学校从这4名同学中随机抽取2名同学接受电视台记者采访，则正好抽到一名男同学和一名女同学的概率为 .
请根据图表提供的信息，解答下列问题：
(1)表中的a＝ ，b＝ (2)请补全频数分布直方图；
(3)若用扇形统计图来描述成绩分布情况，则分数段70≤x＜80对应的圆心角的度数是 ；
(4)竞赛成绩不低于90分的4名同学中正好有2名男同学，2名女同学.学校从这4名同学中随机抽取2名同学接受电视台记者采访，则正好抽到一名男同学和一名女同学的概率为 .
21．如图，一农户要建一个矩形猪舍，猪舍的一边利用长为12m的住房墙，另外三边用25m长的建筑材料围成，为方便进出，在垂直于住房墙的一边留一个1m宽的门，所围矩形猪舍的长、宽分别为多少时，猪舍面积为80m2？
22．如图，AD是△ABC的中线，tan B＝
，cos C＝
，AC＝.求：
（1）BC的长；
（2）sin ∠ADC的值．
，cos C＝，AC＝.求：（1）BC的长；
（2）sin ∠ADC的值．
23．如图，△ABC中，AB＝AC＝1，∠BAC＝45°，△AEF是由△ABC绕点A按顺时针方向旋转得到的，连接BE，CF相交于点D,
（1）求证：BE＝CF ；
（2）当四边形ACDE为菱形时，求BD的长．
（1）求证：BE＝CF ；
（2）当四边形ACDE为菱形时，求BD的长．
24．为满足市场需求，某超市在五月初五“端午节”来临前夕，购进一种品牌粽子，每盒进价是40元．超市规定每盒售价不得少于45元．根据以往销售经验发现；当售价定为每盒45元时，每天可以卖出700盒，每盒售价每提高1元，每天要少卖出20盒．
（1）试求出每天的销售量y（盒）与每盒售价x（元）之间的函数关系式；
（2）当每盒售价定为多少元时，每天销售的利润P（元）最大？最大利润是多少？
（3）为稳定物价，有关管理部门限定：这种粽子的每盒售价不得高于58元．如果超市想要每天获得不低于6000元的利润，那么超市每天至少销售粽子多少盒？
（1）试求出每天的销售量y（盒）与每盒售价x（元）之间的函数关系式；
（2）当每盒售价定为多少元时，每天销售的利润P（元）最大？最大利润是多少？
（3）为稳定物价，有关管理部门限定：这种粽子的每盒售价不得高于58元．如果超市想要每天获得不低于6000元的利润，那么超市每天至少销售粽子多少盒？
25．如图，AB是⊙O的直径，点C为⊙O上一点，AE和过点C的切线互相垂直，垂足为E，AE交⊙O于点D，直线EC交AB的延长线于点P，连接AC，BC，PB：PC=1：2．
（1）求证：AC平分∠BAD；
（2）探究线段PB，AB之间的数量关系，并说明理由；
（3）若AD=3，求△ABC的面积．
（1）求证：AC平分∠BAD；
（2）探究线段PB，AB之间的数量关系，并说明理由；
（3）若AD=3，求△ABC的面积．
26．边长为2的正方形OABC在平面直角坐标系中的位置如图所示，点D是边OA的中点，连接CD，点E在第一象限，且DE⊥DC，DE=DC．以直线AB为对称轴的抛物线过C，E两点．
（1）求抛物线的解析式；
（2）点P从点C出发，沿射线CB每秒1个单位长度的速度运动，运动时间为t秒．过点P作PF⊥CD于点F，当t为何值时，以点P，F，D为顶点的三角形与△COD相似？
（3）点M为直线AB上一动点，点N为抛物线上一动点，是否存在点M，N，使得以点M，N，D，E为顶点的四边形是平行四边形？若存在，请直接写出满足条件的点的坐标；若不存在，请说明理由．
（1）求抛物线的解析式；
（2）点P从点C出发，沿射线CB每秒1个单位长度的速度运动，运动时间为t秒．过点P作PF⊥CD于点F，当t为何值时，以点P，F，D为顶点的三角形与△COD相似？
（3）点M为直线AB上一动点，点N为抛物线上一动点，是否存在点M，N，使得以点M，N，D，E为顶点的四边形是平行四边形？若存在，请直接写出满足条件的点的坐标；若不存在，请说明理由．
