搜索
全一卷
难度系数：0.94 
答案解析
有奖纠错
1．-2的倒数是（ ）
| A．-2 | B． | C． | D．2 |
2．下列几何体中，主视图、左视图、俯视图完全相同的是（ ）
| A．圆锥 | B．六棱柱 | C．球 | D．四棱锥 |
3．一组数据3，3，4，2，8的中位数和平均数分别是（ ）
| A．3和3 | B．3和4 | C．4和3 | D．4和4 |
4．平行四边形的对角线一定具有的性质是（ ）
| A．相等 | B．互相平分 | C．互相垂直 | D．互相垂直且相等 |
5．下列计算正确的是（ ）
A． | B．（ab2）2=ab4 | C．2a+3a=6a | D．a•a3=a4 |
6．如图，C、D是线段AB上的两点，且D是线段AC的中点．若AB=10cm，BC=4cm，则AD的长为（ ）
| A．2cm | B．3cm | C．4cm | D．6cm |
7．一个关于x的一元一次不等式组的解集在数轴上的表示如图，则该不等式组的解集是（ ）
| A．x＞1 | B．x≥1 | C．x＞3 | D．x≥3 |
8．如图，已知菱形ABCD的边长为2，∠DAB=60°，则对角线BD的长是（ ）
| A．1 | B． | C．2 | D． |
9．下列四个圆形图案中，分别以它们所在圆的圆心为旋转中心，顺时针旋转120°后，能与原图形完全重合的是（ ）
A． | B． | C． | D． |
10．函数y=
与y=ax2（a≠0）在同一平面直角坐标系中的图象可能是（ ）
与y=ax2（a≠0）在同一平面直角坐标系中的图象可能是（ ）A． | B． | C． | D． |
11．如图，直线a∥b，直线c分别与a，b相交，若∠1=70°，则∠2=__________ ．
12．抛物线y=3（x﹣2）2+5的顶点坐标是_____ ．
13．如图，A、B、C是⊙O上的三点，∠AOB=100°，则∠ACB=________ 度．
14．已知关于x的一元二次方程2x2﹣3kx+4=0的一个根是1，则k=_______
15．100件外观相同的产品中有5件不合格，现从中任意抽取1件进行检测，抽到不合格产品的概率是_______
16．如图，△ABC中，DE∥BC,
,△ADE的面积为8，则△ABC的面积为______
,△ADE的面积为8，则△ABC的面积为17．如图，点B、E、C、F在一条直线上，AB∥DE，AB=DE，BE=CF，AC=6，则DF=________
18．如图，在平面直角坐标系中，已知点A（2，3），点B（﹣2，1），在x轴上存在点P到A，B两点的距离之和最小，则P点的坐标是________ ．
19．计算：（﹣1）2014+
﹣（
）﹣1+
sin45°．
﹣（
）﹣1+
sin45°．20．先简化，再求值：（1+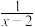
）
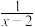，其中x=3．
）
，其中x=3．21．某数学兴趣小组在全校范围内随机抽取了50名同学进行“舌尖上的长沙﹣我最喜爱的长沙小吃”调查活动，将调查问卷整理后绘制成如图所示的不完整条形统计图：
请根据所给信息解答以下问题：
（1）请补全条形统计图；
（2）若全校有2000名同学，请估计全校同学中最喜爱“臭豆腐”的同学有多少人？
（3）在一个不透明的口袋中有四个完全相同的小球，把它们分别标号为四种小吃的序号A、B、C、D，随机地摸出一个小球然后放回，再随机地摸出一个小球，请用列表或画树形图的方法，求出恰好两次都摸到“A”的概率．
请根据所给信息解答以下问题：
（1）请补全条形统计图；
（2）若全校有2000名同学，请估计全校同学中最喜爱“臭豆腐”的同学有多少人？
（3）在一个不透明的口袋中有四个完全相同的小球，把它们分别标号为四种小吃的序号A、B、C、D，随机地摸出一个小球然后放回，再随机地摸出一个小球，请用列表或画树形图的方法，求出恰好两次都摸到“A”的概率．
22．如图，四边形ABCD是矩形，把矩形沿对角线AC折叠，点B落在点E处，CE与AD相交于点O．
（1）求证：△AOE≌△COD；
（2）若∠OCD=30°，AB=，求△AOC的面积．
（1）求证：△AOE≌△COD；
（2）若∠OCD=30°，AB=
，求△AOC的面积．23．为建设“秀美幸福之市”，长沙市绿化提质改造工程正如火如荼地进行，某施工队计划购买甲、乙两种树苗共400棵对芙蓉路的某标段道路进行绿化改造，已知甲种树苗每棵200元，乙种树苗每棵300元．
（1）若购买两种树苗的总金额为90000元，求需购买甲、乙两种树苗各多少棵？
（2）若购买甲种树苗的金额不少于购买一中树苗的金额，至少应购买甲种树苗多少棵？
（1）若购买两种树苗的总金额为90000元，求需购买甲、乙两种树苗各多少棵？
（2）若购买甲种树苗的金额不少于购买一中树苗的金额，至少应购买甲种树苗多少棵？
24．如图，以△ABC的一边AB为直径作⊙O，⊙O与BC边的交点恰好为BC的中点D，过点D作⊙O的切线交AC于点E．
（1）求证：DE⊥AC；
（2）若AB=3DE，求tan∠ACB的值．
（1）求证：DE⊥AC；
（2）若AB=3DE，求tan∠ACB的值．
25．在平面直角坐标系中，我们不妨把横坐标与纵坐标相等的点称为“梦之点”，例如点（﹣1，﹣1），（0，0），（，），…都是“梦之点”，显然，这样的“梦之点”有无数个．
（1）若点P（2，m）是反比例函数y=
（n为常数，n≠0）的图象上的“梦之点”，求这个反比例函数的解析式；
（2）函数y=3kx+s﹣1（k，s是常数）的图象上存在“梦之点”吗？若存在，请求出“梦之点”的坐标；若不存在，请说明理由；
（3）若二次函数y=ax2+bx+1（a，b是常数，a＞0）的图象上存在两个不同的“梦之点”A（x1，x1），B（x2，x2），且满足﹣2＜x1＜2，|x1﹣x2|=2，令t=b2﹣2b+
，试求出t的取值范围．
，），…都是“梦之点”，显然，这样的“梦之点”有无数个．（1）若点P（2，m）是反比例函数y=
（n为常数，n≠0）的图象上的“梦之点”，求这个反比例函数的解析式；（2）函数y=3kx+s﹣1（k，s是常数）的图象上存在“梦之点”吗？若存在，请求出“梦之点”的坐标；若不存在，请说明理由；
（3）若二次函数y=ax2+bx+1（a，b是常数，a＞0）的图象上存在两个不同的“梦之点”A（x1，x1），B（x2，x2），且满足﹣2＜x1＜2，|x1﹣x2|=2，令t=b2﹣2b+
，试求出t的取值范围．26．如图，抛物线
的对称轴为
轴，且经过(0，0)，(
)两点，点P在抛物线上运动，以P为圆心的⊙P经过定点A(0，2)，
（1）求
的值；
（2）求证：点P在运动过程中，⊙P始终与
轴相交；
（3）设⊙P与轴相交于M
，N 
(
＜
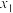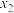)两点，当△AMN为等腰三角形时，求圆心P的纵坐标．
的对称轴为
轴，且经过(0，0)，(
)两点，点P在抛物线上运动，以P为圆心的⊙P经过定点A(0，2)，（1）求
的值； （2）求证：点P在运动过程中，⊙P始终与
轴相交；（3）设⊙P与
轴相交于M
，N 
(
＜
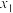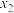)两点，当△AMN为等腰三角形时，求圆心P的纵坐标．
