搜索
全一卷
难度系数：0.94 
答案解析
有奖纠错
1．实数2的倒数是（）
A．﹣ | B．± | C．2 | D． |
2．下列计算正确的是（ ）
| A．2a+5a=7a | B．2x﹣x=1 | C．3+a=3a | D．x2•x3=x6 |
3．下面的几何体中，主视图为圆的是（ ）
A． | B． | C． | D． |
4．2014年“五一”小长假，岳阳楼、君山岛景区接待游客约120000人次，将120000用科学记数法表示为（）
| A．12×104 | B．1.2×105 | C．1.2×106 | D．12万 |
5．不等式组
的解集是（ ）
的解集是（ ）| A．x＞2 | B．x＞1 | C．1＜x＜2 | D．无解 |
6．已知扇形的圆心角为60°，半径为1，则扇形的弧长为（ ）
A． | B．π | C． | D． |
7．下列因式分解正确的是（ ）
| A．x2﹣y2=（x﹣y）2 | B．a2+a+1=（a+1）2 |
| C．xy﹣x=x（y﹣1） | D．2x+y=2（x+y） |
8．如图，已知点A是直线y=x与反比例函数y=（k＞0，x＞0）的交点，B是y=图象上的另一点，BC∥x轴，交y轴于点C．动点P从坐标原点O出发，沿O→A→B→C（图中“→”所示路线）匀速运动，终点为C，过点P作PM⊥x轴，PN⊥y轴，垂足分别为M，N．设四边形OMPN的面积为S，P点运动时间为t，则S关于t的函数图象大致为（ ）
A． | B． | C． | D． |
9．计算：﹣
=_____ ．
=10．方程x2﹣3x+2=0的根是 ．
11．体育测试中，某班某一小组1分钟跳绳成绩如下：176，176，168，150，190，185，180（单位：个），则这组数据的中位数是______ ．
12．从1，2，3，4，5，6，7，8，9这九个自然数中，任取一个数是奇数的概率是_____ ．
13．如图，在△ABC中，点D，E分别是AB，AC的中点且DE=1，则BC= ．
14．如图，若AB∥CD∥EF，∠B=40°，∠F=30°，则∠BCF=_____ ．
15．观察下列一组数：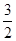
、1、
、
、
…，它们是按一定规律排列的那么这组数的第n个数是 ．（n为正整数）
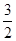、1、
、
、
…，它们是按一定规律排列的那么这组数的第n个数是 ．（n为正整数）16．如图，AB是⊙O的直径，P为AB延长线上的一个动点，过点P作⊙O的切线，切点为C，连接AC，BC，作∠APC的平分线交AC于点D．
下列结论正确的是 （写出所有正确结论的序号）
①△CPD∽△DPA；
②若∠A=30°，则PC=
BC；
③若∠CPA=30°，则PB=OB；
④无论点P在AB延长线上的位置如何变化，∠CDP为定值．
下列结论正确的是 （写出所有正确结论的序号）
①△CPD∽△DPA；
②若∠A=30°，则PC=
BC；③若∠CPA=30°，则PB=OB；
④无论点P在AB延长线上的位置如何变化，∠CDP为定值．
17．计算：|﹣
|+
×
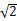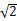+3﹣1﹣22．
|+
×
+3﹣1﹣22．18．解分式方程：
19．在一次蜡烛燃烧实验中，蜡烛燃烧时剩余部分的高度y（cm）与燃烧时间x（h）之间为一次函数关系．根据图象提供的信息，解答下列问题：
（1）求出蜡烛燃烧时y与x之间的函数关系式；
（2）求蜡烛从点燃到燃尽所用的时间．
（1）求出蜡烛燃烧时y与x之间的函数关系式；
（2）求蜡烛从点燃到燃尽所用的时间．
20．某项球类比赛，每场比赛必须分出胜负，其中胜1场得2分，负1场得1分．某队在全部16场比赛中得到25分，求这个队胜、负场数分别是多少．
21．为了响应株洲市政府“低碳出行、绿色出行”的号召，某中学数学兴趣小组在全校2000名学生中就上学方式随机抽取了400名学生进行抽样调查，经统计整理绘制出图a、图b两幅不完整的统计图：
A：步行； B：骑自行车； C：乘公共交通工具； D：乘私家车； E：其他．
请根据统计图提供的信息解答下列问题：
（1）图a中“B”所在扇形的圆心角为 ；
（2）请在图b中把条形统计图补充完整；
（3）请根据样本数据估计全校骑自行车上学的学生人数．
A：步行； B：骑自行车； C：乘公共交通工具； D：乘私家车； E：其他．
请根据统计图提供的信息解答下列问题：
（1）图a中“B”所在扇形的圆心角为 ；
（2）请在图b中把条形统计图补充完整；
（3）请根据样本数据估计全校骑自行车上学的学生人数．
22．如图，矩形ABCD为台球桌面，AD=260cm，AB=130cm，球目前在E点位置，AE=60cm．如果小丁瞄准BC边上的点F将球打过去，经过反弹后，球刚好弹到D点位置．
（1）求证：△BEF∽△CDF；
（2）求CF的长．
（1）求证：△BEF∽△CDF；
（2）求CF的长．
23．数学活动﹣求重叠部分的面积
（1）问题情境：如图①，将顶角为120°的等腰三角形纸片（纸片足够大）的顶点P与等边△ABC的内心O重合，已知OA=2，则图中重叠部分△PAB的面积为 ．
（2）探究1：在（1）的条件下，将纸片绕P点旋转至如图②所示位置，纸片两边分别与AC，AB交于点E，F，图②中重叠部分的面积与图①重叠部分的面积是否相等？如果相等，请给予证明；如果不相等，请说明理由．
（3）探究2：如图③，若∠CAB=α（0°＜α＜90°），AD为∠CAB的角平分线，点P在射线AD上，且AP=2，以P为顶点的等腰三角形纸片（纸片足够大）与∠CAB的两边AC，AB分别交于点E、F，∠EPF=180°﹣α，求重叠部分的面积．（用α或
的三角函数值表示）
（1）问题情境：如图①，将顶角为120°的等腰三角形纸片（纸片足够大）的顶点P与等边△ABC的内心O重合，已知OA=2，则图中重叠部分△PAB的面积为 ．
（2）探究1：在（1）的条件下，将纸片绕P点旋转至如图②所示位置，纸片两边分别与AC，AB交于点E，F，图②中重叠部分的面积与图①重叠部分的面积是否相等？如果相等，请给予证明；如果不相等，请说明理由．
（3）探究2：如图③，若∠CAB=α（0°＜α＜90°），AD为∠CAB的角平分线，点P在射线AD上，且AP=2，以P为顶点的等腰三角形纸片（纸片足够大）与∠CAB的两边AC，AB分别交于点E、F，∠EPF=180°﹣α，求重叠部分的面积．（用α或
的三角函数值表示）24．如图，抛物线经过点A（1，0），B（5，0），C（0，
）三点，设点E（x，y）是抛物线上一动点，且在x轴下方，四边形OEBF是以OB为对角线的平行四边形．
（1）求抛物线的解析式；
（2）当点E（x，y）运动时，试求平行四边形OEBF的面积S与x之间的函数关系式，并求出面积S的最大值；
（3）是否存在这样的点E，使平行四边形OEBF为正方形？若存在，求E点，F点的坐标；若不存在，请说明理由．
）三点，设点E（x，y）是抛物线上一动点，且在x轴下方，四边形OEBF是以OB为对角线的平行四边形．
（1）求抛物线的解析式；
（2）当点E（x，y）运动时，试求平行四边形OEBF的面积S与x之间的函数关系式，并求出面积S的最大值；
（3）是否存在这样的点E，使平行四边形OEBF为正方形？若存在，求E点，F点的坐标；若不存在，请说明理由．
