全一卷
1.﹣2012的相反数是()
| A.﹣2012 | B.2012 | C. | D. |
2.下面四个几何体中,左视图是四边形的几何体共有()


| A.1个 | B.2个 | C.3个 | D.4个 |
3.下列不是必然事件的是( )
| A.角平分线上的点到角两边的距离相等 |
| B.三角形任意两边之和大于第三边 |
| C.面积相等的两个三角形全等 |
| D.三角形内心到三边距离相等 |
4.如图,直线a、b被直线c所截,下列说法正确的是( )


A.当∠1=∠2时,一定有a b b |
B.当a b时,一定有∠1=∠2 b时,一定有∠1=∠2 |
C.当a b时,一定有∠1+∠2=90° b时,一定有∠1+∠2=90° |
D.当∠1+∠2=180°时,一定有a b b |
5.某农户一年的总收入为50000元,如图是这个农户收入的扇形统计图,则该农户的经济作物收入为()


| A.20000元 | B.12500元 | C.15500元 | D.17500元 |
6.实数a、b在数轴上的位置如图所示,且|a|>|b|,则化简 的结果为( )
的结果为( )

 的结果为( )
的结果为( )
| A.2a+b | B.-2a+b | C.b | D.2a-b |
7.顺次连接矩形四边中点所得的四边形一定是( )
| A.正方形 | B.矩形 | C.菱形 | D.等腰梯形 |
8.当a≠0时,函数y=ax+1与函数 在同一坐标系中的图象可能是()
在同一坐标系中的图象可能是()
 在同一坐标系中的图象可能是()
在同一坐标系中的图象可能是()A. | B. |
C. | D. |
9.分解因式8a2-2=__________ .
10.已知 与
与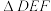 相似且面积比为
相似且面积比为 ,则
,则 与
与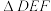 的相似比为
的相似比为_____ .
 与
与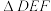 相似且面积比为
相似且面积比为 ,则
,则 与
与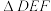 的相似比为
的相似比为11.一组数据是4、x、5、10、11共有五个数,其平均数为7,则这组数据的众数是_______ .
12.2012年5月底,三峡电站三十二台机组全部投产发电,三峡工程圆满实现2250万千瓦的设计发电能力.据此,三峡电站每天能发电约540000000度,用科学记数法表示应为_______ 度.
13.已知m和n是方程2x2﹣5x﹣3=0的两根,则 =
=_______ .
 =
=14.已知圆锥的底面直径和母线长都是10cm,则圆锥的侧面积为 ▲ .
15.已知 ,则x+y=
,则x+y=______ .
 ,则x+y=
,则x+y=16.已知线段AB=6,

| A.D是AB上两点,且AC=DB=1,P是线段CD上一动点,在AB同侧分别作等边三角形APE和等边三角形PBF,G为线段EF的中点,点P由点C移动到点D时,G点移动的路径长度为 |

17.计算: .
.
 .
.18.如图,在方格纸中,以格点连线为边的三角形叫格点三角形,请按要求完成下列操作:先将格点△ABC向右平移4个单位得到△A1B1C1,再将△A1B1C1绕点C1点旋转180°得到△A2B2C2.


19.先化简: ,再用一个你最喜欢的数代替a计算结果.
,再用一个你最喜欢的数代替a计算结果.
 ,再用一个你最喜欢的数代替a计算结果.
,再用一个你最喜欢的数代替a计算结果.20.第七届中博会于2012年5月18日至20日在湖南召开,设立了长沙、株洲、湘潭和张家界4个会展区,聪聪一家用两天时间参观两个会展区:第一天从4个会展区中随机选择一个,第二天从余下3个会展区中再随机选择一个,如果每个会展区被选中的机会均等.
(1)请用画树状图或列表的方法表示出所有可能出现的结果;
(2)求聪聪一家第一天参观长沙会展区,第二天参观张家界会展区的概率;
(3)求张家界会展区被选中的概率.
(1)请用画树状图或列表的方法表示出所有可能出现的结果;
(2)求聪聪一家第一天参观长沙会展区,第二天参观张家界会展区的概率;
(3)求张家界会展区被选中的概率.
21.黄岩岛是我国南海上的一个岛屿,其平面图如图甲所示,小明据此构造出该岛的一个数学模型如图乙所示,其中∠A=∠D=90°,AB=BC=15千米,CD= 千米,请据此解答如下问题:
千米,请据此解答如下问题:

(1)求该岛的周长和面积;(结果保留整数,参考数据 )
)
(2)求∠ACD的余弦值.
 千米,请据此解答如下问题:
千米,请据此解答如下问题:
(1)求该岛的周长和面积;(结果保留整数,参考数据
 )
)(2)求∠ACD的余弦值.
22.某公园出售的一次性使用门票,每张10元,为了吸引更多游客,新近推出购买“个人年票”的售票活动(从购买日起,可供持票者使用一年).年票分
| A.B两类:A类年票每张100元,持票者每次进入公园无需再购买门票;B类年票每张50元,持票者进入公园时需再购买每次2元的门票.某游客一年中进入该公园至少要超过多少次时,购买A类年票最合算? |
23.阅读材料:对于任何实数,我们规定符号 的意义是
的意义是 =ad﹣bc.例如:
=ad﹣bc.例如: =1×4﹣2×3=﹣2,
=1×4﹣2×3=﹣2, =(﹣2)×5﹣4×3=﹣22.
=(﹣2)×5﹣4×3=﹣22.
(1)按照这个规定,请你计算 的值;
的值;
(2)按照这个规定,请你计算:当x2﹣4x+4=0时, 的值.
的值.
 的意义是
的意义是 =ad﹣bc.例如:
=ad﹣bc.例如: =1×4﹣2×3=﹣2,
=1×4﹣2×3=﹣2, =(﹣2)×5﹣4×3=﹣22.
=(﹣2)×5﹣4×3=﹣22.(1)按照这个规定,请你计算
 的值;
的值;(2)按照这个规定,请你计算:当x2﹣4x+4=0时,
 的值.
的值.24.如图,⊙O的直径AB=4,C为圆周上一点,AC=2,过点C作⊙O的切线DC,P点为优弧 上一动点(不与A.C重合).
上一动点(不与A.C重合).
(1)求∠APC与∠ACD的度数;
(2)当点P移动到CB弧的中点时,求证:四边形OBPC是菱形.
(3)P点移动到什么位置时,△APC与△ABC全等,请说明理由.
 上一动点(不与A.C重合).
上一动点(不与A.C重合).(1)求∠APC与∠ACD的度数;
(2)当点P移动到CB弧的中点时,求证:四边形OBPC是菱形.
(3)P点移动到什么位置时,△APC与△ABC全等,请说明理由.

25.如图,抛物线 与x轴交于
与x轴交于
(2)求直线AB的解析式;
(3)若反比例函数 的图象过点D,求k值;
的图象过点D,求k值;
(4)两动点P、Q同时从点A出发,分别沿AB.AO方向向B.O移动,点P每秒移动1个单位,点Q每秒移动 个单位,设△POQ的面积为S,移动时间为t,问:S是否存在最大值?若存在,求出这个最大值,并求出此时的t值;若不存在,请说明理由.
个单位,设△POQ的面积为S,移动时间为t,问:S是否存在最大值?若存在,求出这个最大值,并求出此时的t值;若不存在,请说明理由.
 与x轴交于
与x轴交于| A.A两点,与y轴交于点B,OB=4.点O关于直线AB的对称点为D,E为线段AB的中点. (1)分别求出点 | B.点B的坐标; |
(3)若反比例函数
 的图象过点D,求k值;
的图象过点D,求k值;(4)两动点P、Q同时从点A出发,分别沿AB.AO方向向B.O移动,点P每秒移动1个单位,点Q每秒移动
 个单位,设△POQ的面积为S,移动时间为t,问:S是否存在最大值?若存在,求出这个最大值,并求出此时的t值;若不存在,请说明理由.
个单位,设△POQ的面积为S,移动时间为t,问:S是否存在最大值?若存在,求出这个最大值,并求出此时的t值;若不存在,请说明理由.
 搜索
搜索
 难度系数:0.94
难度系数:0.94  答案解析
答案解析
 有奖纠错
有奖纠错
