搜索
全一卷
难度系数：0.94 
答案解析
有奖纠错
1．2014的相反数是（ ）
| A．﹣2014 | B．﹣ | C．2014 | D． |
2．下列运算正确的是（ ）
| A．x2•x3=x6 | B．（x3）3=x9 | C．x2+x2=x4 | D．x6÷x3=x2 |
3．函数 y=
中自变量x的取值范围为（）
中自变量x的取值范围为（）| A．x≥0 | B．x≥﹣2 | C．x≥2 | D．x≤﹣2 |
4．方程组
的解是（）
的解是（）A． | B． | C． | D． |
5．下列图形既是轴对称图形，又是中心对称图形的是（ ）
A． | B． |
C． | D． |
6．若两圆的半径分别为2cm和6cm，圆心距为了8cm，则两圆的位置关系为（ ）
| A．外切 | B．相交 | C．内切 | D．外离 |
7．实施新课改以来，某班学生经常采用“小组合作学习”的方式进行学习，学习委员小兵每周对各小组合作学习的情况进行了综合评分．下表是其中一周的统计数据：
这组数据的中位数和众数分别是
| 组 别 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 分 值 | 90 | 95 | 90 | 88 | 90 | 92 | 85 |
这组数据的中位数和众数分别是
| A．88，90 | B．90，90 | C．88，95 | D．90，95 |
8．下列命题中，错误的是（ ）
| A．平行四边形的对角线互相平分 |
| B．菱形的对角线互相垂直平分 |
| C．矩形的对角线相等且互相垂直平分 |
| D．角平分线上的点到角两边的距离相等 |
9．如图，把一块等腰直角三角板的直角顶点放在直尺的一边上，如果∠1=40°，那么∠2=（ ）
| A．40° | B．45° | C．50° | D．60° |
10．一次函数y＝kx－k(k＜0)的图象大致是( )
A． | B． | C． | D． |
11．五月初五是我国的传统节日﹣端午节．今年端午节，小王在“百度”搜索引擎中输入“端午节”，搜索到与之相关的结果约为75100000个，75100000用科学记数法表示为____ ．
12．按照如图所示的操作步骤，若输入的值为3，则输出的值为____ ．
13．已知关于x的方程2x+a﹣5=0的解是x=2，则a的值为_______ ．
14．不等式组
的解集为______ ．
的解集为15．如图，要使平行四边形ABCD是矩形，则应添加的条件是_____ （添加一个条件即可）．
16．如图，M为反比例函数y=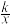
的图象上的一点，MA垂直y轴，垂足为A，
的面积为2，则k的值为_______ ．
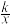的图象上的一点，MA垂直y轴，垂足为A，
的面积为2，则k的值为
17．如图，小明用长为3m的竹竿CD作测量工具，测量学校旗杆AB的高度，移动竹竿，使竹竿与旗杆的距离DB=12m，则旗杆AB的高为____ m．
18．五张分别写有﹣1，2，0，﹣4，5的卡片（除数字不同以外，其余都相同），现从中任意取出一张卡片，则该卡片上的数字是负数的概率是_________ ．
19．如图是一组有规律的图案，第1个图案由4个▲组成，第2个图案由7个▲组成，第3个图案由10个▲组成，第4个图案由13个▲组成，……，则第n（n为正整数）个图案由________ 个▲组成．
20．如图，平行四边形ABCD的对角线AC、BD交于点O，点E是AD的中点，△BCD的周长为18，则△DEO的周长是_______ ．
21．先化简
÷（1﹣
），再从不等式2x﹣3＜7的正整数解中选一个使原式有意义的数代入求值．
÷（1﹣
），再从不等式2x﹣3＜7的正整数解中选一个使原式有意义的数代入求值．22．如图，有小岛A和小岛B，轮船以45km/h的速度由C向B航行，在C处测得A的方位角为北偏东60°，测得B的方位角为南偏东45°，轮船航行2小时后到达小岛B处，在B处测得小岛A在小岛B的正北方向．求小岛A与小岛B之间的距离（结果保留整数，参考数据：
≈1.41，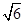
≈2.45）
≈1.41，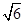
≈2.45）
23．“中国梦”是中华民族每一个人的梦，也是每一个中小学生的梦，各中小学开展经典诵读活动，无疑是“中国梦”教育这一宏大乐章里的响亮音符，学校在经典诵读活动中，对全校学生用A、B、C、D四个等级进行评价，现从中抽取若干个学生进行调查，绘制出了两幅不完整的统计图，请你根据图中信息解答下列问题：
（1）共抽取了多少个学生进行调查？
（2）将图甲中的折线统计图补充完整．
（3）求出图乙中B等级所占圆心角的度数．
（1）共抽取了多少个学生进行调查？
（2）将图甲中的折线统计图补充完整．
（3）求出图乙中B等级所占圆心角的度数．
24．娄底到长沙的距离约为180km，小刘开着小轿车，小张开着大货车，都从娄底去长沙，小刘比张晚出发1小时，最后两车同时到达长沙，已知小轿车的速度是大货车速度的1.5倍．
(1)求小轿车和大货车的速度各是多少？（列方程解答）
(2)当小刘出发时，求小张离长沙还有多远？
(1)求小轿车和大货车的速度各是多少？（列方程解答）
(2)当小刘出发时，求小张离长沙还有多远？
25．如图，在⊙O中，AB，CD是直径，BE是切线，B为切点，连接AD，BC，BD．
（1）求证：△ABD≌△CDB；
（2）若∠DBE=37°，求∠ADC的度数．
（1）求证：△ABD≌△CDB；
（2）若∠DBE=37°，求∠ADC的度数．
26．如图，抛物线y=x2+mx+（m﹣1）与x轴交于点A（x1，0），B（x2，0），x1＜x2，与y轴交于点C（0，c），且满足x12+x22+x1x2=7．
（1）求抛物线的解析式；
（2）在抛物线上能不能找到一点P，使∠POC=∠PCO？若能，请求出点P的坐标；若不能，请说明理由．
（1）求抛物线的解析式；
（2）在抛物线上能不能找到一点P，使∠POC=∠PCO？若能，请求出点P的坐标；若不能，请说明理由．
27．如图甲，在△ABC中，∠ACB=90°，AC=4cm，BC=3cm．如果点P由点B出发沿BA方向向点A匀速运动，同时点Q由点A出发沿AC方向向点C匀速运动，它们的速度均为1cm/s．连接PQ，设运动时间为t（s）（0＜t＜4），解答下列问题：
（1）设△APQ的面积为S，当t为何值时，S取得最大值，S的最大值是多少；
（2）如图乙，连接PC，将△PQC沿QC翻折，得到四边形PQP′C，当四边形PQP′C为菱形时，求t的值；
（3）当t为何值时，△APQ是等腰三角形．
（1）设△APQ的面积为S，当t为何值时，S取得最大值，S的最大值是多少；
（2）如图乙，连接PC，将△PQC沿QC翻折，得到四边形PQP′C，当四边形PQP′C为菱形时，求t的值；
（3）当t为何值时，△APQ是等腰三角形．
