全一卷
1.﹣3的相反数是( )
A. | B. | C. | D. |
2.习近平总书记提出精准扶贫战略以来,各地积极推进精准扶贫,加大帮扶力度,全国脱贫人口数不断增加,脱贫人口接近 人,将数据
人,将数据 用科学记数法表示为( )
用科学记数法表示为( )
 人,将数据
人,将数据 用科学记数法表示为( )
用科学记数法表示为( )A. | B. | C. | D. |
3.下列图形是轴对称图形但不是中心对称图形的是( )
A. | B. | C. | D. |
4.下列计算中正确的是( )
A. | B. | C. | D. |
5.如图, ,若
,若 ,则
,则 的度数是( )
的度数是( )

 ,若
,若 ,则
,则 的度数是( )
的度数是( )
A. | B. | C. | D. |
6.如图,在 中,
中,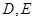 分别为
分别为 边上的中点,则
边上的中点,则 与
与 的面积之比是( )
的面积之比是( )

 中,
中,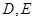 分别为
分别为 边上的中点,则
边上的中点,则 与
与 的面积之比是( )
的面积之比是( )
A. | B. | C. | D. |
7.把函数 的图象,经过怎样的平移变换以后,可以得到函数
的图象,经过怎样的平移变换以后,可以得到函数 的图象( )
的图象( )
 的图象,经过怎样的平移变换以后,可以得到函数
的图象,经过怎样的平移变换以后,可以得到函数 的图象( )
的图象( )A.向左平移 个单位,再向下平移 个单位,再向下平移 个单位 个单位 |
B.向左平移 个单位,再向上平移 个单位,再向上平移 个单位 个单位 |
C.向右平移 个单位,再向上平移 个单位,再向上平移 个单位 个单位 |
D.向右平移 个单位,再向下平移 个单位,再向下平移 个单位 个单位 |
8.如图,在⊙ 中,半径
中,半径 垂直弦
垂直弦 于
于 ,点
,点 在⊙
在⊙ 上,
上, ,则半径
,则半径 等于( )
等于( )

 中,半径
中,半径 垂直弦
垂直弦 于
于 ,点
,点 在⊙
在⊙ 上,
上, ,则半径
,则半径 等于( )
等于( )
A. | B. | C. | D. |
9.已知点 是直线
是直线 与双曲线
与双曲线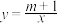 (
( 为常数)一支的交点,过点
为常数)一支的交点,过点 作
作 轴的垂线,垂足为
轴的垂线,垂足为 ,且
,且 ,则
,则 的值为( )
的值为( )
 是直线
是直线 与双曲线
与双曲线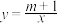 (
( 为常数)一支的交点,过点
为常数)一支的交点,过点 作
作 轴的垂线,垂足为
轴的垂线,垂足为 ,且
,且 ,则
,则 的值为( )
的值为( )A. | B. | C. | D. |
10.如图,从一张腰长为 ,顶角为
,顶角为 的等腰三角形铁皮
的等腰三角形铁皮 中剪出一个最大的扇形
中剪出一个最大的扇形 ,用此剪下的扇形铁皮围成一个圆锥的侧面(不计损耗),则该圆锥的底面半径为( )
,用此剪下的扇形铁皮围成一个圆锥的侧面(不计损耗),则该圆锥的底面半径为( )

 ,顶角为
,顶角为 的等腰三角形铁皮
的等腰三角形铁皮 中剪出一个最大的扇形
中剪出一个最大的扇形 ,用此剪下的扇形铁皮围成一个圆锥的侧面(不计损耗),则该圆锥的底面半径为( )
,用此剪下的扇形铁皮围成一个圆锥的侧面(不计损耗),则该圆锥的底面半径为( )
A. | B. | C. | D. |
11.把一些书分给几名同学,如果每人分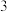 本,那么余
本,那么余 本;如果前面的每名同学分
本;如果前面的每名同学分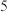 本,那么最后一人就分不到
本,那么最后一人就分不到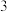 本,这些书有______本,共有______人.( )
本,这些书有______本,共有______人.( )
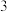 本,那么余
本,那么余 本;如果前面的每名同学分
本;如果前面的每名同学分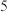 本,那么最后一人就分不到
本,那么最后一人就分不到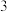 本,这些书有______本,共有______人.( )
本,这些书有______本,共有______人.( )A. 本, 本, 人 人 | B. 本, 本, 人 人 | C. 本, 本,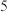 人 人 | D. 本, 本, 人 人 |
12.如图,在矩形 中,
中, ,动点
,动点 满足
满足 ,则点
,则点 到
到 两点距离之和
两点距离之和 的最小值为( )
的最小值为( )

 中,
中, ,动点
,动点 满足
满足 ,则点
,则点 到
到 两点距离之和
两点距离之和 的最小值为( )
的最小值为( )
A. | B. | C. | D. |
13.因式分解:
______ .

14.一元二次方程 的根是_____.
的根是_____.
 的根是_____.
的根是_____.15.若实数 满足
满足 ,且
,且 恰好是直角三角形的两条边,则该直角三角形的斜边长为
恰好是直角三角形的两条边,则该直角三角形的斜边长为_____ .
 满足
满足 ,且
,且 恰好是直角三角形的两条边,则该直角三角形的斜边长为
恰好是直角三角形的两条边,则该直角三角形的斜边长为16.如图,在 中,
中, ,点
,点 是边
是边 上的一点,
上的一点, 于
于 ,则边
,则边 的长为
的长为_____ .

 中,
中, ,点
,点 是边
是边 上的一点,
上的一点, 于
于 ,则边
,则边 的长为
的长为
17.如图,把一张长为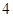 ,宽为
,宽为 的矩形纸片,沿对角线折叠,则重叠部分的面积为_____.
的矩形纸片,沿对角线折叠,则重叠部分的面积为_____.
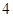 ,宽为
,宽为 的矩形纸片,沿对角线折叠,则重叠部分的面积为_____.
的矩形纸片,沿对角线折叠,则重叠部分的面积为_____.
18.观察下列式子
第 个式子:
个式子:
第 个式子:
个式子:
第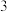 个式子:
个式子:
……
请写出第 个式子:
个式子:_____ .
第
 个式子:
个式子:
第
 个式子:
个式子:
第
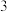 个式子:
个式子:
……
请写出第
 个式子:
个式子:19.计算 .
.
 .
.20.如图,点E、C在线段BF上,BE=CF,AB=DE,AC=DF.求证:∠ABC=∠DEF.


21.某校为研究学生的课余爱好情况,采取抽样调查的方法,从阅读、运动、娱乐、上网等四个方面调查了若干学生的兴趣爱好,并将调查的结果绘制成如下两幅不完整的统计图,请你根据图中提供的信息解答下列问题:

(1)在这次研究中,一共调查了 名学生;若该校共有 名学生,估计全校爱好运动的学生共有 名;
名学生,估计全校爱好运动的学生共有 名;
(2)补全条形统计图,并计算阅读部分圆心角是 ;
(3)在全校同学中随机选出一名学生参加演讲比赛,用频率估计概率,则选出的恰好是爱好阅读的学生概率是 .

(1)在这次研究中,一共调查了 名学生;若该校共有
 名学生,估计全校爱好运动的学生共有 名;
名学生,估计全校爱好运动的学生共有 名;(2)补全条形统计图,并计算阅读部分圆心角是 ;
(3)在全校同学中随机选出一名学生参加演讲比赛,用频率估计概率,则选出的恰好是爱好阅读的学生概率是 .
22.列方程(组)解应用题
绿水青山就是金山银山,为了创造良好的生态环境,防止水土流失,某村计划在荒坡上种树 棵,由于青年志愿者支援,实际每天种树的棵树是原计划的
棵,由于青年志愿者支援,实际每天种树的棵树是原计划的 倍,结果提前
倍,结果提前 天完成任务,则原计划每天种树多少棵?
天完成任务,则原计划每天种树多少棵?
绿水青山就是金山银山,为了创造良好的生态环境,防止水土流失,某村计划在荒坡上种树
 棵,由于青年志愿者支援,实际每天种树的棵树是原计划的
棵,由于青年志愿者支援,实际每天种树的棵树是原计划的 倍,结果提前
倍,结果提前 天完成任务,则原计划每天种树多少棵?
天完成任务,则原计划每天种树多少棵?23.由我国完全自主设计,自主建造的首艘国产航母于2018年5月成功完成首次海上试验任务.如图,航母由西向东航行,到达 处时,测得小岛
处时,测得小岛 在北偏东
在北偏东 方向上,航行
方向上,航行 海里到达
海里到达 点,这时测得小岛
点,这时测得小岛 在北偏东
在北偏东 方向上,小岛
方向上,小岛 周围
周围 海里内有暗礁,如果航母不改变航线继续向东航行,有没有触礁危险?请说明理由.
海里内有暗礁,如果航母不改变航线继续向东航行,有没有触礁危险?请说明理由.

 处时,测得小岛
处时,测得小岛 在北偏东
在北偏东 方向上,航行
方向上,航行 海里到达
海里到达 点,这时测得小岛
点,这时测得小岛 在北偏东
在北偏东 方向上,小岛
方向上,小岛 周围
周围 海里内有暗礁,如果航母不改变航线继续向东航行,有没有触礁危险?请说明理由.
海里内有暗礁,如果航母不改变航线继续向东航行,有没有触礁危险?请说明理由.
24.如图,在 中.
中. ,以
,以 为直径的⊙
为直径的⊙ 分别交
分别交 于点
于点 ,点
,点 在
在 的延长线上,且
的延长线上,且 .
.

(1)求证: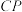 是⊙
是⊙ 的切线;
的切线;
(2)若 ,求点
,求点 到
到 的距离.
的距离.
 中.
中. ,以
,以 为直径的⊙
为直径的⊙ 分别交
分别交 于点
于点 ,点
,点 在
在 的延长线上,且
的延长线上,且 .
.
(1)求证:
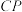 是⊙
是⊙ 的切线;
的切线;(2)若
 ,求点
,求点 到
到 的距离.
的距离.25.已知:如图,抛物线y=ax2+bx+3与坐标轴分别交于点A,B(﹣3,0),C(1,0),点P是线段AB上方抛物线上的一个动点.
(1)求抛物线解析式;
(2)当点P运动到什么位置时,△PAB的面积最大?
(3)过点P作x轴的垂线,交线段AB于点D,再过点P作PE∥x轴交抛物线于点E,连接DE,请问是否存在点P使△PDE为等腰直角三角形?若存在,求点P的坐标;若不存在,说明理由.

(1)求抛物线解析式;
(2)当点P运动到什么位置时,△PAB的面积最大?
(3)过点P作x轴的垂线,交线段AB于点D,再过点P作PE∥x轴交抛物线于点E,连接DE,请问是否存在点P使△PDE为等腰直角三角形?若存在,求点P的坐标;若不存在,说明理由.

 搜索
搜索
 难度系数:0.94
难度系数:0.94  答案解析
答案解析
 有奖纠错
有奖纠错
