搜索
全一卷
难度系数：0.94 
答案解析
有奖纠错
1．下列四个数中，比0小的数是【 】
A． | B．0 | C．1 | D．2 |
2．x是2的相反数，︱y︱=3，则x－y的值是【 】
A． | B．1 | C．或5 | D．1或 |
3．如图，一个等边三角形纸片，剪去一个角后得到一个四边形，则图中∠α+∠β的度数是（ ）
A． | B． | C． | D． |
4．已知
，则
的值是（ ）
，则
的值是（ ）A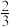． | B． | C． | D． |
5．下列多项式能分解因式的是（ ）
A． | B． | C． | D． |
6．如图，有四张不透明的卡片除正面的算式不同外，其余完全相同，将它们背面朝上洗匀后，从中随机抽取一张，则抽到得卡片上算式正确的概率是【 】
A． | B． | C． | D．1 |
7．设a、b、c表示三种不同物体的质量，用天枰称两次，情况如图所示，则这三种物体的质量从小到大排序正确的是【 】
A． | B． | C． | D． |
8．如图，已知AB∥CD，∠DFE=135°，则∠ABE的度数为（）
A． | B． | C． | D． |
9．下列命题：①圆周角等于圆心角的一半；②x=2是方程x－1=1的解；③平行四边形既是中心对称图形又是轴对称图形；④
的算术平方根是4。其中真命题的个数有【 】
的算术平方根是4。其中真命题的个数有【 】| A．1 | B．2 | C．3 | D．4 |
10．一家鞋店在一段时间内销售了某种男鞋200双，各种尺码鞋的销售量如下表所示：
一般来讲，鞋店老板比较关心哪种尺码的鞋最畅销，也就是关心卖出的鞋的尺码组成的一组数据是（）
| 尺码/厘米 | 23 | 23.5 | 24 | 24.5 | 25 | 25.5 | 26 |
| 销售量/双 | 5 | 10 | 22 | 39 | 56 | 43 | 25 |
一般来讲，鞋店老板比较关心哪种尺码的鞋最畅销，也就是关心卖出的鞋的尺码组成的一组数据是（）
| A．平均数 | B．中位数 | C．众数 | D．方差 |
11．雅西高速公路于2012年4月29日正式通车，西昌到成都全长420千米，一辆小汽车和一辆客车同时从西昌、成都两地相向开出，经过2.5小时相遇，相遇时，小汽车比客车多行驶70千米，设小汽车和客车的平均速度分别为x千米/小时和y千米/小时，则下列方程组正确的是（）
A． | B． |
C． | D． |
12．如图，在平面直角坐标系中，⊙O的半径为1，则直线
与⊙O的位置关系是（）
与⊙O的位置关系是（）
| A．相离 | B．相切 | C．相交 | D．以上三种情况都有可能 |
13．在函数
中，自变量x的取值范围是___ ．
中，自变量x的取值范围是14．整式A与m2－2mn＋n2的和是（m＋n)2，则A为_______ ．
15．如图，已知点A在反比例函数图象上，AM⊥x轴于点M，且△AOM的面积为1，则反比例函数的解析式为_______ .
16．某商品的售价是528元，商家出售一件这样的商品可获利润是进价的10%～20%，设进价为x元，则x的取值范围是_______ ．
17．如图，小正方形构成的网络中，半径为1的⊙O在格点上，则图中阴影部分两个小扇形的面积之和为______ （结果保留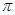
）．
）．
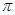18．计算：
；
；19．如图，梯形ABCD是直角梯形．
（1）直接写出点A、B、C、D的坐标；
（2）画出直角梯形ABCD关于y轴的对称图形，使它与梯形ABCD构成一个等腰梯形．
（3）将（2）中的等腰梯形向上平移四个单位长度，画出平移后的图形．（不要求写作法）
（1）直接写出点A、B、C、D的坐标；
（2）画出直角梯形ABCD关于y轴的对称图形，使它与梯形ABCD构成一个等腰梯形．
（3）将（2）中的等腰梯形向上平移四个单位长度，画出平移后的图形．（不要求写作法）
20．如图，在矩形ABCD中，AB=6，AD=12，点E在AD边上，且AE=8，EF⊥BE交CD于F
（1）求证：△ABE∽△DEF；
（2）求EF的长．
（1）求证：△ABE∽△DEF；
（2）求EF的长．
21．某校学生去春游，在风景区看到一棵汉柏树，不知这棵汉柏树有多高，下面是两位同学的一段对话：
小明：我站在此处看树顶仰角为
．
小华：我站在此处看树顶仰角为
．
小明：我们的身高都是1.6m.
小华：我们相距20m．
请你根据这两位同学的对话，计算这棵汉柏树的高度．
（参考数据：
，
，结果保留三个有效数字）
小明：我站在此处看树顶仰角为
．小华：我站在此处看树顶仰角为
．小明：我们的身高都是1.6m.
小华：我们相距20m．
请你根据这两位同学的对话，计算这棵汉柏树的高度．
（参考数据：
，
，结果保留三个有效数字）
22．吸烟有害健康，为配合“戒烟”运动，某校组织同学们在社区开展了“你支持哪种戒烟方式”的随机问卷调查，并将调查结果绘制成两幅不完整的统计图：
根据统计图解答下列问题：
（1）同学们一共调查了多少人？
（2）将条形统计图补充完整。
（3）若该社区有1万人，请你估计大约有多少人支持“警示戒烟”这种方式？
（4）为了让更多的市民增强“戒烟”意识，同学们在社区做了两期“警示戒烟”的宣传。若每期宣传后，市民支持“警示戒烟”的平均增长率为20%，则两期宣传后支持“警示戒烟”的市民约有多少人？
根据统计图解答下列问题：
（1）同学们一共调查了多少人？
（2）将条形统计图补充完整。
（3）若该社区有1万人，请你估计大约有多少人支持“警示戒烟”这种方式？
（4）为了让更多的市民增强“戒烟”意识，同学们在社区做了两期“警示戒烟”的宣传。若每期宣传后，市民支持“警示戒烟”的平均增长率为20%，则两期宣传后支持“警示戒烟”的市民约有多少人？
23．在学习轴对称的时候，老师让同学们思考课本中的探究题．
如图（1），要在燃气管道l上修建一个泵站，分别向A、B两镇供气．泵站修在管道的什么地方，可使所用的输气管线最短？
你可以在l上找几个点试一试，能发现什么规律？你可以在
上找几个点试一试，能发现什么规律？
聪明的小华通过独立思考，很快得出了解决这个问题的正确办法．他把管道l看成一条直线（图（2）），问题就转化为，要在直线l上找一点P，使AP与BP的和最小．他的做法是这样的：
①作点B关于直线l的对称点B′．
②连接AB′交直线l于点P，则点P为所求．
请你参考小华的做法解决下列问题．如图在△ABC中，点D、E分别是AB、AC边的中点，BC=6，BC边上的高为4，请你在BC边上确定一点P，使△PDE得周长最小．
（1）在图中作出点P（保留作图痕迹，不写作法）．
（2）请直接写出△PDE周长的最小值：
．
如图（1），要在燃气管道l上修建一个泵站，分别向A、B两镇供气．泵站修在管道的什么地方，可使所用的输气管线最短？
你可以在l上找几个点试一试，能发现什么规律？你可以在
上找几个点试一试，能发现什么规律？
聪明的小华通过独立思考，很快得出了解决这个问题的正确办法．他把管道l看成一条直线（图（2）），问题就转化为，要在直线l上找一点P，使AP与BP的和最小．他的做法是这样的：
①作点B关于直线l的对称点B′．
②连接AB′交直线l于点P，则点P为所求．
请你参考小华的做法解决下列问题．如图在△ABC中，点D、E分别是AB、AC边的中点，BC=6，BC边上的高为4，请你在BC边上确定一点P，使△PDE得周长最小．
（1）在图中作出点P（保留作图痕迹，不写作法）．
（2）请直接写出△PDE周长的最小值：
．
24．某商场计划购进冰箱、彩电进行销售．相关信息如下表：
（1）若商场用80000元购进冰箱的数量与用64000元购进彩电的数量相等，求表中a的值．
（2）为了满足市场需要求，商场决定用不超过9万元采购冰箱、彩电共50台，且冰箱的数量不少于彩电数量的
．
①该商场有哪几种进货方式？
②若该商场将购进的冰箱、彩电全部售出，获得的最大利润为w元，请用所学的函数知识求出w的值．
| | 进价（元/台） | 售价（元/台） |
| 冰箱 |  | 2500 |
| 彩电 |  | 2000 |
（1）若商场用80000元购进冰箱的数量与用64000元购进彩电的数量相等，求表中a的值．
（2）为了满足市场需要求，商场决定用不超过9万元采购冰箱、彩电共50台，且冰箱的数量不少于彩电数量的
．①该商场有哪几种进货方式？
②若该商场将购进的冰箱、彩电全部售出，获得的最大利润为w元，请用所学的函数知识求出w的值．
25．对于正数
，规定
，例如：
，
，则
_______ ．
，规定
，例如：
，
，则
26．如图，在四边形ABCD中，AC=BD=6，E、F、G、H分别是AB、BC、CD、DA的中点，则EG2+FH2=______.
27．如图，已知直径为OA的⊙P与x轴交于O、A两点，点B、C把
三等分，连接PC并延长PC交y轴于点D（0，3）．
求证：（1）△POD≌△ABO；
（2）若直线l：y=kx+b经过圆心P和D，求直线l的解析式
三等分，连接PC并延长PC交y轴于点D（0，3）．求证：（1）△POD≌△ABO；
（2）若直线l：y=kx+b经过圆心P和D，求直线l的解析式
28．如图，在平面直角坐标系中，直线y=x＋4与x轴、y轴分别交于A、B两点，抛物线y=－x2＋bx＋c经过A、B两点，并与x轴交于另一点C（点C点A的右侧），点P是抛物线上一动点．
（1）求抛物线的解析式及点C的坐标；
（2）若点P在第二象限内，过点P作PD⊥轴于D，交AB于点E．当点P运动到什么位置时，线段PE最长？此时PE等于多少？
（3）如果平行于x轴的动直线l与抛物线交于点Q，与直线AB交于点N，点M为OA的中点，那么是否存在这样的直线l，使得△MON是等腰三角形？若存在，请求出点Q的坐标；若不存在，请说明理由．
（1）求抛物线的解析式及点C的坐标；
（2）若点P在第二象限内，过点P作PD⊥轴于D，交AB于点E．当点P运动到什么位置时，线段PE最长？此时PE等于多少？
（3）如果平行于x轴的动直线l与抛物线交于点Q，与直线AB交于点N，点M为OA的中点，那么是否存在这样的直线l，使得△MON是等腰三角形？若存在，请求出点Q的坐标；若不存在，请说明理由．
