搜索
全一卷
难度系数：0.85 
答案解析
有奖纠错
1．如图所示的几何体，其主视图是（ ）
A． | B． | C． | D． |
2．函数
的自变量x的取值范围是（ ）
的自变量x的取值范围是（ ）A． | B． | C． | D． |
3．如图，a∥b，∠1=55°，∠2=65°，则∠3的大小是（）
| A．50° | B．55° | C．60° | D．65° |
4．世界杯足球赛正在巴西如火如荼地进行，赛前有人预测，巴西国家队夺冠的概率是90%．对他的说法理解正确的是（ ）
| A．巴西队一定会夺冠 | B．巴西队一定不会夺冠 |
| C．巴西队夺冠的可能性很大 | D．巴西队夺冠的可能性很小 |
5．下列运算正确的是（ ）
A． | B． | C． | D． |
6．若反比例函数
的图象过点（2，1），则这个函数的图象一定过点（ ）
的图象过点（2，1），则这个函数的图象一定过点（ ）A． | B． | C． | D． |
7．在
ABCD中，AC，BD是对角线，如果添加一个条件，即可推出ABCD是矩形，那么这个条件是（ ）
ABCD中，AC，BD是对角线，如果添加一个条件，即可推出ABCD是矩形，那么这个条件是（ ）| A．AB=BC | B．AC=BD | C．AC⊥BD | D．AB⊥BD |
8．点
均在抛物线
上，下列说法正确的是（ ）
均在抛物线上，下列说法正确的是（ ）A．若 ，则 | B．若 ，则 |
C．若 ，则 | D．若 ，则 |
9．如图，BC是⊙O的直径，AD⊥BC，若∠D=36°，则∠BAD的度数是（ ）
| A．72° | B．54° | C．45° | D．36° |
10．如图，点A，点B的坐标分别是
，将线段AB绕A旋转180°后得到线段AC，则点C的坐标为（）
，将线段AB绕A旋转180°后得到线段AC，则点C的坐标为（）
A． | B． | C． | D． |
11．点P从点O出发，按逆时针方向沿周长为l的图形运动一周，O、P两点间的距离y与点走过的路程x的函数关系如图，那么点P所走的图形是（ ）
A． | B． | C． | D． |
12．计算：
.
.13．分解因式： x2－4＝ .
14．一个不透明的袋子中装有4个红球，6个白球，2个黑球，这些球除颜色不同外没有任何区别. 随机地从这个袋子中摸出一个球，这个球为红球的概率是 .
15．如图，DE为△ABC的中位线，点F在DE上，且∠AFB为直角，若AB=6，BC=8，则EF的长为 .
16．如图，小明从A地沿北偏东60°方向走2千米到B地，再从B地向正南方向走3千米到C地，此时小明距离A地_______ 千米（结果可保留根号）.
17．在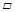
ABCD中，
，AE平分∠BAC，交BC于E. 沿AE将△ABE折叠，点B的对应点为F，连结EF并延长交AD于G，EG将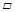ABCD分为面积相等的两部分. 则
_______ .
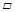ABCD中，
，AE平分∠BAC，交BC于E. 沿AE将△ABE折叠，点B的对应点为F，连结EF并延长交AD于G，EG将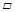ABCD分为面积相等的两部分. 则
18．计算：
(说明：本题不允许使用计算器计算)
(说明：本题不允许使用计算器计算)19．解不等式组：
20．如图，△ABC是等边三角形，D是BC的中点.
（1）作图：
①过B作AC的平行线BH；
②过D作BH的垂线，分别交AC，BH，AB的延长线于E，F，G.
（2）在图中找出一对全等三角形，并证明你的结论.
（1）作图：
①过B作AC的平行线BH；
②过D作BH的垂线，分别交AC，BH，AB的延长线于E，F，G.
（2）在图中找出一对全等三角形，并证明你的结论.
21．乔丹体育用品商店开展“超级星期六”促销活动：运动服8折出售，运动鞋每双减20元. 活动期间，标价为480元的某款运动服装（含一套运动服和一双运动鞋）价格为400元.问该款运动服和运动鞋的标价各是多少元？
22．某县为了解初中生对安全知识掌握情况，抽取了50名初中生进行安全知识测试，并将测试成绩进行统计分析，绘成如下的频数分布表和频数分布直方图（未完成）：
（1）完成频数分布直方图；
（2）这个样本数据的中位数在第 组；
（3）若将各组的组中值视为该组的平均成绩，则此次测试的平均成绩为 ；
（4）若将90分以上（含90分）定为“优秀”等级，则该县10000名初中生中，获“优秀”等级的学生约为 人.
（1）完成频数分布直方图；
（2）这个样本数据的中位数在第 组；
（3）若将各组的组中值视为该组的平均成绩，则此次测试的平均成绩为 ；
（4）若将90分以上（含90分）定为“优秀”等级，则该县10000名初中生中，获“优秀”等级的学生约为 人.
23．小明购买了一部新手机，到某通讯公司咨询移动电话资费情况，准备办理入网手续，该通讯公司工作人员向他介绍两种不同的资费方案：
（1）分别写出方案一，二中，月话费（月租费与通话费的总和）y（单位：元）与通话时间x（单位：分）的函数关系式；
（2）画出（1）中两个函数的图象；
（3）若小明通话时间为200分钟左右，他应该选择哪种资费方案最省钱.
| 方案代号 | 月租费（元） | 免费时间（分） | 超过免费时间的通话费（元/分） |
| 一 | 10 | 0 | 0.20 |
| 二 | 30 | 80 | 0.15 |
（1）分别写出方案一，二中，月话费（月租费与通话费的总和）y（单位：元）与通话时间x（单位：分）的函数关系式；
（2）画出（1）中两个函数的图象；
（3）若小明通话时间为200分钟左右，他应该选择哪种资费方案最省钱.
24．⊙O的半径为5，AB是⊙O的直径，点C在⊙O上，点D在直线AB上.
（1）如图（1），已知∠BCD=∠BAC，求证：CD是⊙O的切线；
（2）如图（2），CD与⊙O交于另一点E，BD：DE：EC=2；3：5求圆心O到直线CD的距离；
（3）若图（2）中的点D是直线AB上的动点，点D在运动过程中，会出现在C，D，E三点中，其中一点是另两点连线的中点的情况，问这样的情况出现几次？
（1）如图（1），已知∠BCD=∠BAC，求证：CD是⊙O的切线；
（2）如图（2），CD与⊙O交于另一点E，BD：DE：EC=2；3：5求圆心O到直线CD的距离；
（3）若图（2）中的点D是直线AB上的动点，点D在运动过程中，会出现在C，D，E三点中，其中一点是另两点连线的中点的情况，问这样的情况出现几次？
25．如图（1），在平面直角坐标系xOy中，抛物线
与x轴交于
，与y轴交于C(0，3)，顶点为D(1,4)，对称轴为DE.
（1）抛物线的解析式是 ；
（2）如图（2），点P是AD上的一个动点，
是P关于DE的对称点，连结PE，过作F∥PE交x轴于F. 设
，求y关于x的函数关系式，并求y的最大值；
（3）在（1）中的抛物线上是否存在点Q，使△BCQ成为以BC为直角边的直角三角形？若存在，求出Q的坐标；若不存在，请说明理由.
与x轴交于
，与y轴交于C(0，3)，顶点为D(1,4)，对称轴为DE. （1）抛物线的解析式是 ；
（2）如图（2），点P是AD上的一个动点，
是P关于DE的对称点，连结PE，过作F∥PE交x轴于F. 设
，求y关于x的函数关系式，并求y的最大值；（3）在（1）中的抛物线上是否存在点Q，使△BCQ成为以BC为直角边的直角三角形？若存在，求出Q的坐标；若不存在，请说明理由.
