全一卷
1.﹣ 的相反数是( )
的相反数是( )
 的相反数是( )
的相反数是( )A.﹣ | B.﹣ | C. | D. |
2. 的结果是()
的结果是()
 的结果是()
的结果是()A. | B. | C. | D. |
3.要使二次根式 有意义,x必须满足( )
有意义,x必须满足( )
 有意义,x必须满足( )
有意义,x必须满足( )| A.x≤2 | B.x≥2 | C.x<2 | D.x>2 |
4.一个正方体的每个面都有一个汉字,其平面展开图如图所示,那么在该正方体中和“值”字相对的字是( )


| A.记 | B.观 | C.心 | D.间 |
5.三角形两边长分别为3和6,第三边的长是方程x2﹣13x+36=0的一个根,则该三角形的周长为( )
| A.13 | B.15 | C.18 | D.13或18 |
6.均匀地向一个容器注水,最后将容器注满 在注水过程中,水的高度h随时间t的变化规律如图所示,这个容器的形状可能是
在注水过程中,水的高度h随时间t的变化规律如图所示,这个容器的形状可能是


 在注水过程中,水的高度h随时间t的变化规律如图所示,这个容器的形状可能是
在注水过程中,水的高度h随时间t的变化规律如图所示,这个容器的形状可能是


A. | B. | C. | D. |
7.只用下列哪一种正多边形,可以进行平面镶嵌( )
| A.正五边形 | B.正六边形 | C.正八边形 | D.正十边形 |
8.解分式方程 时,去分母后变形正确的为( )
时,去分母后变形正确的为( )
 时,去分母后变形正确的为( )
时,去分母后变形正确的为( )| A.2+(x+2)=3(x-1) |
| B.2-x+2=3(x-1) |
| C.2-(x+2)=3 |
| D.2-(x+2)=3(x-1) |
9.如图,斜面AC的坡度(CD与AD的比)为1:2,AC=3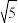 米,坡顶有旗杆BC,旗杆顶端B点与A点有一条彩带相连.若AB=10米,则旗杆BC的高度为( )
米,坡顶有旗杆BC,旗杆顶端B点与A点有一条彩带相连.若AB=10米,则旗杆BC的高度为( )

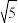 米,坡顶有旗杆BC,旗杆顶端B点与A点有一条彩带相连.若AB=10米,则旗杆BC的高度为( )
米,坡顶有旗杆BC,旗杆顶端B点与A点有一条彩带相连.若AB=10米,则旗杆BC的高度为( )
| A.5米 | B.6米 | C.8米 | D.(3+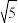 )米 )米 |
10.将一副三角尺(在 中,∠ACB=
中,∠ACB= ,∠B=
,∠B= ;在
;在 中,∠EDF=
中,∠EDF= ,∠E=
,∠E= )如图摆放,点D为AB的中点,DE交AC于点P,DF经过点C.将
)如图摆放,点D为AB的中点,DE交AC于点P,DF经过点C.将 绕点D顺时针方向旋转角
绕点D顺时针方向旋转角 ,
, 交AC于点M,
交AC于点M, 交BC于点N,则
交BC于点N,则 的值为()
的值为()

 中,∠ACB=
中,∠ACB= ,∠B=
,∠B= ;在
;在 中,∠EDF=
中,∠EDF= ,∠E=
,∠E= )如图摆放,点D为AB的中点,DE交AC于点P,DF经过点C.将
)如图摆放,点D为AB的中点,DE交AC于点P,DF经过点C.将 绕点D顺时针方向旋转角
绕点D顺时针方向旋转角 ,
, 交AC于点M,
交AC于点M, 交BC于点N,则
交BC于点N,则 的值为()
的值为()
A. | B. | C. | D. |
11.2014年我国国内生产总值约为636000亿元,用科学计数法表示2014年国内生产总值约为___ 亿元.
12.分解因式: =
=_____________ .
 =
=13.甲乙两地9月上旬的日平均气温如图所示,则甲乙两地这10天日平均气温的方差大小关系为
___  (填
(填 或
或 ).
).


 (填
(填 或
或 ).
).
14.在平面直角坐标系中,以原点为中心,把点A(4,5)逆时针旋转90O,得到的点B的坐标为____ .
15.若 ,
,
 ,
,
 ,
,
……
则 .
.
 ,
, ,
, ,
,……
则
 .
.16.(本题满分5分)计算:

17.某学校初三年级男生共200人,随机抽取10名测量他们的身高为(单位:cm):
181、176、169、155、163、175、173、167、165、166.
(1)求这10名男生的平均身高和上面这组数据的中位数;
(2)估计该校初三年级男生身高高于170cm的人数;
(3)从身高为181、176、175、173的男生中任选2名,求身高为181cm的男生被抽中的概率.
181、176、169、155、163、175、173、167、165、166.
(1)求这10名男生的平均身高和上面这组数据的中位数;
(2)估计该校初三年级男生身高高于170cm的人数;
(3)从身高为181、176、175、173的男生中任选2名,求身高为181cm的男生被抽中的概率.
18.小明到服装店参加社会实践活动,服装店经理让小明帮助解决以下问题:
服装店准备购进甲乙两种服装,甲种每件进价80元,售价120元;乙种每件进价60元,售价90元.计划购进两种服装共100件,其中甲种服装不少于65件.
(1)若购进这100件服装的费用不得超过7500,则甲种服装最多购进多少件?
(2)在(1)的条件下,该服装店对甲种服装以每件优惠a(0<a<20)元的价格进行优惠促销活动,乙种服装价格不变,那么该服装店应如何调整进货方案才能获得最大利润?
服装店准备购进甲乙两种服装,甲种每件进价80元,售价120元;乙种每件进价60元,售价90元.计划购进两种服装共100件,其中甲种服装不少于65件.
(1)若购进这100件服装的费用不得超过7500,则甲种服装最多购进多少件?
(2)在(1)的条件下,该服装店对甲种服装以每件优惠a(0<a<20)元的价格进行优惠促销活动,乙种服装价格不变,那么该服装店应如何调整进货方案才能获得最大利润?
19.如图,在△ABC中,AB=AC,∠DAC是△ABC的一个外角.
实践与操作:
根据要求尺规作图,并在图中标明相应字母(保留作图痕迹,不写作法).

(1)作∠DAC的平分线AM;
(2)作线段AC的垂直平分线,与AM交于点F,与BC边交于点E,连接AE、CF.
猜想并证明:判断四边形AECF的形状并加以证明.
实践与操作:
根据要求尺规作图,并在图中标明相应字母(保留作图痕迹,不写作法).

(1)作∠DAC的平分线AM;
(2)作线段AC的垂直平分线,与AM交于点F,与BC边交于点E,连接AE、CF.
猜想并证明:判断四边形AECF的形状并加以证明.
20.在矩形 中,
中, ,
, .分别以
.分别以 所在直线为
所在直线为 轴和
轴和 轴,建立如图所示的平面直角坐标系.
轴,建立如图所示的平面直角坐标系. 是边
是边 上一点,过点
上一点,过点 的反比例函数
的反比例函数 图象与
图象与 边交于点
边交于点 .
.

(1)请用k表示点E,F的坐标;
(2)若 的面积为
的面积为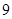 ,求反比例函数的解析式.
,求反比例函数的解析式.
 中,
中, ,
, .分别以
.分别以 所在直线为
所在直线为 轴和
轴和 轴,建立如图所示的平面直角坐标系.
轴,建立如图所示的平面直角坐标系. 是边
是边 上一点,过点
上一点,过点 的反比例函数
的反比例函数 图象与
图象与 边交于点
边交于点 .
.
(1)请用k表示点E,F的坐标;
(2)若
 的面积为
的面积为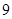 ,求反比例函数的解析式.
,求反比例函数的解析式.21.在一个三角形中,各边和它所对角的正弦的比相等.即 .利用上述结论可以求解如下题目.如:
.利用上述结论可以求解如下题目.如:
在 中,若
中,若 ,
, ,
, ,求
,求 .
.
解:在 中,
中,

问题解决:
如图,甲船以每小时 海里的速度向正北方航行,当甲船位于
海里的速度向正北方航行,当甲船位于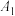 处时,乙船位于甲船的北偏西
处时,乙船位于甲船的北偏西 方向的
方向的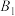 处,且乙船从
处,且乙船从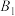 处按北偏东
处按北偏东 方向匀速直线航行,当甲船航行
方向匀速直线航行,当甲船航行 分钟到达
分钟到达 处时,乙船航行到甲船的北偏西
处时,乙船航行到甲船的北偏西 方向的
方向的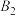 处,此时两船相距
处,此时两船相距 海里.
海里.

(1)判断 的形状,并给出证明.
的形状,并给出证明.
(2)乙船每小时航行多少海里?
 .利用上述结论可以求解如下题目.如:
.利用上述结论可以求解如下题目.如:在
 中,若
中,若 ,
, ,
, ,求
,求 .
.解:在
 中,
中,

问题解决:
如图,甲船以每小时
 海里的速度向正北方航行,当甲船位于
海里的速度向正北方航行,当甲船位于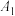 处时,乙船位于甲船的北偏西
处时,乙船位于甲船的北偏西 方向的
方向的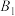 处,且乙船从
处,且乙船从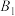 处按北偏东
处按北偏东 方向匀速直线航行,当甲船航行
方向匀速直线航行,当甲船航行 分钟到达
分钟到达 处时,乙船航行到甲船的北偏西
处时,乙船航行到甲船的北偏西 方向的
方向的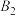 处,此时两船相距
处,此时两船相距 海里.
海里.
(1)判断
 的形状,并给出证明.
的形状,并给出证明.(2)乙船每小时航行多少海里?
22.(本题满分11分)如图,⊙E的圆心E(3,0),半径为5,⊙E与y轴相交于A、B两点(点A在点B的上方),与x轴的正半轴相交于点C;直线l的解析式为y= x+4,与x轴相交于点D;以C为顶点的抛物线经过点B.
x+4,与x轴相交于点D;以C为顶点的抛物线经过点B.

(1)求抛物线的解析式;
(2)判断直线l与⊙E的位置关系,并说明理由;
(3)动点P在抛物线上,当点P到直线l的距离最小时,求出点P的坐标及最小距离.
 x+4,与x轴相交于点D;以C为顶点的抛物线经过点B.
x+4,与x轴相交于点D;以C为顶点的抛物线经过点B.
(1)求抛物线的解析式;
(2)判断直线l与⊙E的位置关系,并说明理由;
(3)动点P在抛物线上,当点P到直线l的距离最小时,求出点P的坐标及最小距离.
 搜索
搜索
 难度系数:0.85
难度系数:0.85  答案解析
答案解析
 有奖纠错
有奖纠错
