搜索
全一卷
难度系数：0.94 
答案解析
有奖纠错
1．（3分）计算﹣2+1的结果是（）
| A．﹣3 | B．﹣1 | C．3 | D．1 |
2．下列计算正确的是（ ）
A． | B． |
C． | D． |
3．如图，AB∥CD，∠A=46°，∠C=27°，则∠AEC的大小应为（）
| A．19° | B．29° | C．63° | D．73° |
4．一组数据2，3，1，2，2的中位数、众数和方差分别是（）
| A．1，2，0.4 | B．2，2，4.4 | C．2，2，0.4 | D．2，1，0.4 |
5．如图是由6个同样大小的正方体摆成的几何体．将正方体①移走后，所得几何体（ ）
| A．主视图改变，左视图改变 | B．俯视图不变，左视图不变 |
| C．俯视图改变，左视图改变 | D．主视图改变，左视图不变 |
6．估计
的运算结果应在哪两个连续自然数之间( )
的运算结果应在哪两个连续自然数之间( )| A．5和6 | B．6和7 | C．7和8 | D．8和9 |
7．下列一元二次方程中，有两个相等实数根的是（）
A． | B． |
C． | D． |
8．已知两点A（5，6）、B（7，2），先将线段AB向左平移一个单位，再以原点O为位似中心，在第一象限内将其缩小为原来的
得到线段CD，则点A的对应点C的坐标为（ ）
得到线段CD，则点A的对应点C的坐标为（ ）| A．（2，3） | B．（3，1） | C．（2，1） | D．（3，3） |
9．如图，在矩形ABCD中，AB=5，BC=7，点E为BC上一动点，把△ABE沿AE折叠，当点B的对应点B′落在∠ADC的角平分线上时，则点B′到BC的距离为（）
| A．1或2 | B．2或3 | C．3或4 | D．4或5 |
10．如图，在直角坐标系中，直线
与坐标轴交于A、B两点，与双曲线
（
）交于点C，过点C作CD⊥x轴，垂足为D，且OA=AD，则以下结论：
①
；
②当0＜x＜3时，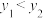
；
③如图，当x=3时，EF=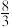
；
④当x＞0时，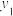
随x的增大而增大，
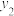随x的增大而减小．
其中正确结论的个数是（ ）
与坐标轴交于A、B两点，与双曲线
（
）交于点C，过点C作CD⊥x轴，垂足为D，且OA=AD，则以下结论：①
；②当0＜x＜3时，
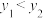；③如图，当x=3时，EF=
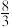；④当x＞0时，
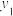随x的增大而增大，
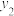随x的增大而减小．其中正确结论的个数是（ ）
| A．1 | B．2 | C．3 | D．4 |
11．太阳半径约为696000千米，数字696000用科学记数法表示为_______ 千米．
12．一个三角形的两边长分别是2和3，若它的第三边长为奇数，则这个三角形的周长为________ ．
13．小球在如图所示的地板上自由地滚动，并随机地停留在某块方砖上，那么小球最终停留在黑色区域的概率是_____________________ ．
14．如图是矗立在高速公路水平地面上的交通警示牌，经测量得到如下数据：AM＝4米，AB＝8米，∠MAD＝45°，∠MBC＝30°，则警示牌的高CD为＿米.（结果精确到0.1米，参考数据：
≈1.41，
≈1.73）
≈1.41，
≈1.73）
15．一个足球被从地面向上踢出，它距地面的高度h（m）与足球被踢出后经过的时间t（s）之间具有函数关系
，已知足球被踢出后经过4s落地，则足球距地面的最大高度是______ m．
，已知足球被踢出后经过4s落地，则足球距地面的最大高度是16．如图，在Rt△AOB中，∠AOB＝90°，AO＝，BO＝1，AB的垂直平分线交AB于点E，交射线BO于点F．点P从点A出发沿射线AO以每秒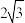
个单位的速度运动，同时点Q从点O出发沿OB方向以每秒1个单位的速度运动，当点Q到达点B时，点P、Q同时停止运动．设运动的时间为t秒．
（1）当t＝____ 时，PQ∥EF；
（2）若P、Q关于点O的对称点分别为P′、Q′，当线段P′Q′与线段EF有公共点时，t的取值范围是_________ ．
，BO＝1，AB的垂直平分线交AB于点E，交射线BO于点F．点P从点A出发沿射线AO以每秒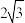
个单位的速度运动，同时点Q从点O出发沿OB方向以每秒1个单位的速度运动，当点Q到达点B时，点P、Q同时停止运动．设运动的时间为t秒．
（1）当t＝
（2）若P、Q关于点O的对称点分别为P′、Q′，当线段P′Q′与线段EF有公共点时，t的取值范围是
17．先化简，再求值：
，其中
．
，其中
．18．如图，在
中，点
是
的中点，点
、
分别是线段
及其延长线上，且
，给出下列条件：①
；②
；③
，从中选择一个条件使四边形
是菱形，并给出证明，你选择的条件是________ （只填写序号）．
中，点
是
的中点，点
、
分别是线段
及其延长线上，且
，给出下列条件：①
；②
；③
，从中选择一个条件使四边形
是菱形，并给出证明，你选择的条件是
19．为响应国家节能减排的号召，鼓励居民节约用电，各省先后出台了居民用电“阶梯价格”制度，如下表是某省的电价标准(每月).例如：方女士家5月份用电500度，电费＝180×0.6＋220×二档电价＋100×三档电价＝352元；李先生家5月份用电460度，交费316元.请问表中二档电价、三档电价各是多少？
20．某校申报“跳绳特色运动”学校一年后，抽样调查了部分学生的“1分钟跳绳”成绩，并制成了下面的频数分布直方图（每小组含最小值，不含最大值）和扇形图．
（1）补全频数分布直方图，扇形图中m= ；
（2）若把每组中各个数据用这组数据的中间值代替（如A组80≤x＜100的中间值是（
=90次），则这次调查的样本平均数是多少；
（3）如果“1分钟跳绳”成绩大于或等于120次为优秀，那么该校2100名学生中“1分钟跳绳”成绩为优秀的大约有多少人．
（1）补全频数分布直方图，扇形图中m= ；
（2）若把每组中各个数据用这组数据的中间值代替（如A组80≤x＜100的中间值是（
=90次），则这次调查的样本平均数是多少；（3）如果“1分钟跳绳”成绩大于或等于120次为优秀，那么该校2100名学生中“1分钟跳绳”成绩为优秀的大约有多少人．
21．在学习概率的课堂上，老师提出问题：只有一张电影票，小明和小刚想通过抽取扑克牌的游戏来决定谁去看电影，请你设计一个对小明和小刚都公平的方案．
甲同学的方案：将红桃2、3、4、5四张牌背面向上，小明先抽一张，小刚从剩下的三张牌中抽一张，若两张牌上的数字之和是奇数，则小明看电影，否则小刚看电影．
（1）甲同学的方案公平吗？请用列表或画树状图的方法说明；
（2）乙同学将甲的方案修改为只用红桃2、3、4三张牌，抽取方式及规则不变，乙的方案公平吗？（只回答，不说明理由）
甲同学的方案：将红桃2、3、4、5四张牌背面向上，小明先抽一张，小刚从剩下的三张牌中抽一张，若两张牌上的数字之和是奇数，则小明看电影，否则小刚看电影．
（1）甲同学的方案公平吗？请用列表或画树状图的方法说明；
（2）乙同学将甲的方案修改为只用红桃2、3、4三张牌，抽取方式及规则不变，乙的方案公平吗？（只回答，不说明理由）
22．如图，在△ABC中，以AB为直径的⊙O交AC于点D，过点D作DE⊥BC于点E，且∠BDE=∠A．
（1）判断DE与⊙O的位置关系，并说明理由；
（2）若AC=16，tanA=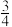
，求⊙O的半径．
（1）判断DE与⊙O的位置关系，并说明理由；
（2）若AC=16，tanA=
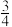，求⊙O的半径．23．某农场急需氨肥8 t，在该农场南北方向分别有A，B两家化肥公司，A公司有氨肥3 t，每吨售价750元；B公司有氨肥7 t，每吨售价700元，汽车每千米的运输费用b(单位：元/千米)与运输质量a(单位：t)的关系如图所示．
(1)根据图象求出b关于a的函数表达式(写出自变量的取值范围)．
(2)若农场到B公司的路程是农场到A公司路程的2倍，农场到A公司的路程为m(km)，设农场从A公司购买x(t)氨肥，购买8 t氨肥的总费用为y元(总费用＝购买铵肥的费用＋运输费用)，求出y关于x的函数表达式(m为常数)，并向农场建议总费用最低的购买方案．
(1)根据图象求出b关于a的函数表达式(写出自变量的取值范围)．
(2)若农场到B公司的路程是农场到A公司路程的2倍，农场到A公司的路程为m(km)，设农场从A公司购买x(t)氨肥，购买8 t氨肥的总费用为y元(总费用＝购买铵肥的费用＋运输费用)，求出y关于x的函数表达式(m为常数)，并向农场建议总费用最低的购买方案．
24．（10分）问题：如图（1），在Rt△ACB中，∠ACB=90°，AC=CB，∠DCE=45°，试探究AD、DE、EB满足的等量关系．
[探究发现]
小聪同学利用图形变换，将△CAD绕点C逆时针旋转90°得到△CBH，连接EH，由已知条件易得∠EBH=90°，∠ECH=∠ECB+∠BCH=∠ECB+∠ACD=45°．根据“边角边”，可证△CEH≌ ，得EH=E
[探究发现]
小聪同学利用图形变换，将△CAD绕点C逆时针旋转90°得到△CBH，连接EH，由已知条件易得∠EBH=90°，∠ECH=∠ECB+∠BCH=∠ECB+∠ACD=45°．根据“边角边”，可证△CEH≌ ，得EH=E
| A． 在Rt△HBE中，由 定理，可得BH2+EB2=EH2，由BH=AD，可得AD、DE、EB之间的等量关系是 ． [实践运用] （1）如图（2），在正方形ABCD中，△AEF的顶点E、F分别在BC、CD边上，高AG与正方形的边长相等，求∠EAF的度数； （2）在（1）条件下，连接BD，分别交AE、AF于点M、N，若BE=2，DF=3，BM=2  ，运用小聪同学探究的结论，求正方形的边长及MN的长. |
25．如图，已知经过点D（2，
）的抛物线
（m为常数，且m＞0）与x轴交于点A、B（点A位于B的左侧），与y轴交于点
）的抛物线
（m为常数，且m＞0）与x轴交于点A、B（点A位于B的左侧），与y轴交于点A． （1）填空：m的值为 ，点A的坐标为 ； （2）根据下列描述，用尺规完成作图（保留作图痕迹，不写作法）：连接AD，在x轴上方作射线AE，使∠BAE=∠BAD，过点D作x轴的垂线交射线AE于点E； （3）动点M、N分别在射线AB、AE上，求ME+MN的最小值； （4）t是过点A平行于y轴的直线，P是抛物线上一点，过点P作l的垂线，垂足为点G，请你探究：是否存在点P，使以P、G、A为顶点的三角形与△ABD相似？若存在，求出点P的坐标；若不存在，说明理由． |
