全一卷
1. 的倒数是()
的倒数是()
 的倒数是()
的倒数是()A. | B. | C. | D. |
2.下列各数: ,sin30°,
,sin30°, ,
, ,其中无理数的个数是()
,其中无理数的个数是()
 ,sin30°,
,sin30°, ,
, ,其中无理数的个数是()
,其中无理数的个数是()| A.1个 | B.2个 | C.3个 | D.4个 |
3.三角形的下列线段中,能将三角形的面积分成相等两部分的是【 】
| A.中线 | B.角平分线 | C.高 | D.中位线 |
4.由5个相同的正方体搭成的几何体如图所示,则它的左视图是( )


A. | B. | C. | D. |
5.下列实验中,概率最大的是【 】
| A.抛掷一枚质地均匀的硬币,出现正面; |
| B.抛掷一枚质地均匀的正方体骰子(六个面分别刻有数字1到6),掷出的点数为奇数; |
| C.在一副洗匀的扑克(背面朝上)中任取一张,恰好为方块; |
| D.三张同样的纸片,分别写有数字2,3,4,和匀后背面朝上,任取一张恰好为偶数 |
6.已知两圆的半径分别为1和3,当这两圆内含时,圆心距d的范围是()
| A.0<d<2 | B.1<d<2 | C.0<d<3 | D.0≤d<2 |
7.如图,在等边△ABC中,点P从A点出发,沿着A→B→C的路线运动,△ACP的面积为S,运动时间为t,则S与t的图像是( )


A. | B. |
C. | D. |
8. 对于二次函数 ,下列说法正确的是( )
,下列说法正确的是( )
 ,下列说法正确的是( )
,下列说法正确的是( )| A.图象的开口向下 | B.当x>1时,y随x的增大而减小 |
| C.当x<1时,y随x的增大而减小 | D.图象的对称轴是直线x=-1 |
9.不能判定一个四边形是平行四边形的条件是( ).
| A.两组对边分别平行 | B.一组对边平行,另一组对边相等 |
| C.一组对边平行且相等 | D.两组对边分别相等 |
10.如图,已知AD是△ABC的BC边上的高,下列能使△ABD≌△ACD的条件是( )


| A.AB=AC | B.∠BAC=90° | C.BD=AC | D.∠B=45° |
11.因式分解:a2-9=_____________ .
12.在2012年清明假期间,巴中火车站发送旅客1.6万余人次,将1.6万用科学计数法表示为______
13.已知一个圆的半径为5cm,则它的内接正六边形的边长为 ▲
14.函数 中,自变量x的取值范围是
中,自变量x的取值范围是_____
 中,自变量x的取值范围是
中,自变量x的取值范围是15.已知a、b、c是△ABC三边的长,且满足关系式 ,则△ABC的形状为
,则△ABC的形状为_______ .
 ,则△ABC的形状为
,则△ABC的形状为16.在巴中创建“国家森林城市”的植树活动中初三某班某小组五名同学植树数分
别为5,6,6,6,7,则这组数据的众数为_______
别为5,6,6,6,7,则这组数据的众数为
17.有一个底面半径为3cm,母线长10cm的圆锥,则其侧面积是______ cm2
18.观察下面一列数:1,-2,3,-4,5,-6,……,根据你发现的规律,第2012个数是_____
19.如图,在等腰梯形ABCD中,AD∥BC,BD⊥DC,点E是BC的中点,且DE∥AB,则∠BCD的度数是________


20.若关于x的方程 有增根,则m的值是
有增根,则m的值是_____
 有增根,则m的值是
有增根,则m的值是21.计算:

22.解方程:

23.解不等式组 ,并写出不等式组的整数解
,并写出不等式组的整数解
 ,并写出不等式组的整数解
,并写出不等式组的整数解24.先化简,再求值: 其中
其中
 其中
其中
25.①如图1,在每个小方格都是边长为1个单位长度的正方形方格纸中有△OAB,
请将△OAB绕点O顺时针旋转90°,画出旋转后的△OA’B’;
②折纸:有一张矩形纸片ABCD(如图2),要将点D沿某条直线翻折180°,恰好落在BC边上的点D’
处,,请在图中作出该直线.
请将△OAB绕点O顺时针旋转90°,画出旋转后的△OA’B’;
②折纸:有一张矩形纸片ABCD(如图2),要将点D沿某条直线翻折180°,恰好落在BC边上的点D’
处,,请在图中作出该直线.

26.我市建设森林城市需要大量的树苗,某生态示范园负责对甲、乙、丙、丁四
个品种的树苗共500株进行树苗成活率试验,从中选取成活率高的品种进行推广。通过实验得知:丙种树
苗成活率为89.6%,把实验数据绘制成下列两幅统计图(部分信息未给出)。

(1)实验所用的乙种树苗的数量是__________株;
(2)求出丙种树苗的成活数,并把图2补充完整;
(3)你认为应选哪一种树苗进行推广?请通过计算说明理由。
个品种的树苗共500株进行树苗成活率试验,从中选取成活率高的品种进行推广。通过实验得知:丙种树
苗成活率为89.6%,把实验数据绘制成下列两幅统计图(部分信息未给出)。

(1)实验所用的乙种树苗的数量是__________株;
(2)求出丙种树苗的成活数,并把图2补充完整;
(3)你认为应选哪一种树苗进行推广?请通过计算说明理由。
27.一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=30°,∠A=45°,AC= ,试求CD的长.
,试求CD的长.

 ,试求CD的长.
,试求CD的长.
28.如图,四边形ABCD是平行四边形,以AB为直径的⊙O经过点D,E是⊙O
上一点,且∠AED=45°。
(1)判断CD与⊙O的位置关系,并说明理由;
(2)若⊙O的半径为6cm,AE=10cm,求∠ADE的正弦值。
上一点,且∠AED=45°。
(1)判断CD与⊙O的位置关系,并说明理由;
(2)若⊙O的半径为6cm,AE=10cm,求∠ADE的正弦值。

29.某商品的进价为每件50元,售价为每件60元,每个月可卖出200件.如果每
件商品的售价上涨1元,则每个月少卖10件(每件售价不能高于72元).设每件商品的售价上涨x元(x
为整数),每个月的销售利润为y元,
(1)求y与x的函数关系式,并直接写出x的取值范围;
(2)每件商品的售价定为多少元时,每个月可获得最大利润?最大月利润是多少元?
件商品的售价上涨1元,则每个月少卖10件(每件售价不能高于72元).设每件商品的售价上涨x元(x
为整数),每个月的销售利润为y元,
(1)求y与x的函数关系式,并直接写出x的取值范围;
(2)每件商品的售价定为多少元时,每个月可获得最大利润?最大月利润是多少元?
30.如图,在平面直角坐标系中,一次函数 的图象与y轴交于点A,与x轴交于点B,与反比例函数
的图象与y轴交于点A,与x轴交于点B,与反比例函数 的图象分别交于点M,N,已知△AOB的面积为1,点M的纵坐标为2,
的图象分别交于点M,N,已知△AOB的面积为1,点M的纵坐标为2,
(1)求一次函数和反比例函数的解析式;
(2)直接写出 时x的取值范围.
时x的取值范围.
 的图象与y轴交于点A,与x轴交于点B,与反比例函数
的图象与y轴交于点A,与x轴交于点B,与反比例函数 的图象分别交于点M,N,已知△AOB的面积为1,点M的纵坐标为2,
的图象分别交于点M,N,已知△AOB的面积为1,点M的纵坐标为2,(1)求一次函数和反比例函数的解析式;
(2)直接写出
 时x的取值范围.
时x的取值范围.
31.如图,在平面直角坐标系中,点A,C分别在x轴,y轴上,四边形ABCO
为矩形,AB=16,点D与点A关于y轴对称,tan∠ACB=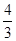 ,点E,F分别是线段AD,AC上的动点(点
,点E,F分别是线段AD,AC上的动点(点
E不与点A,D重合),且∠CEF=∠ACB。
(1)求AC的长和点D的坐标;
(2)说明△AEF与△DCE相似;
(3)当△EFC为等腰三角形时,求点E的坐标。
为矩形,AB=16,点D与点A关于y轴对称,tan∠ACB=
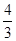 ,点E,F分别是线段AD,AC上的动点(点
,点E,F分别是线段AD,AC上的动点(点E不与点A,D重合),且∠CEF=∠ACB。
(1)求AC的长和点D的坐标;
(2)说明△AEF与△DCE相似;
(3)当△EFC为等腰三角形时,求点E的坐标。

 搜索
搜索
 难度系数:0.94
难度系数:0.94  答案解析
答案解析
 有奖纠错
有奖纠错
