搜索
全一卷
难度系数：0.94 
答案解析
有奖纠错
1．
的结果是（）
的结果是（）| A．－9 | B．0 | C．9 | D．－6 |
2．已知∠α和∠β是对顶角，若∠α＝30°，则∠β的度数为（ ）
| A．30° | B．60° | C．70° | D．150° |
3．有一组数据：1，3，3，4，5，这组数据的众数为( )
| A．1 | B．3 | C．4 | D．5 |
4．若式子
可在实数范围内有意义，则x的取值范围是（）
可在实数范围内有意义，则x的取值范围是（）| A．x≤－4 | B．x≥－4 | C．x≤4 | D．x≥4 |
5．如图，一个圆形转盘被分成6个圆心角都为60°的扇形，任意转动这个转盘1次，当转盘停止转动时，指针指向阴影区域的概率是（ ）
A． | B． | C． | D． |
6．如图，在△ABC中，点D在BC上，AB=AD=DC，∠B=80°，则∠C的度数为（ ）
| A．30° | B．40° | C．45° | D．60° |
7．下列关于x的方程有实数根的是（ ）
| A．x2－x＋1＝0 | B．x2＋x＋1＝0 |
| C．(x－1)(x＋2)＝0 | D．(x－1)2＋1＝0 |
8．二次函数y＝ax2＋bx－1(a≠0)的图象经过点(1，1)．则代数式1－a－b的值为（）
| A．－3 | B．－1 | C．2 | D．5 |
9．如图，港口A在观测站O的正东方向，OA＝4km．某船从港口A出发，沿北偏东15°方向航行一段距离后到达B处，此时从观测站O处测得该船位于北偏东60°的方向，则该船航行的距离（即AB的长）为（ ）
| A．4km | B．2 km | C．2 km | D．（＋1）km |
10．如图，△AOB为等腰三角形，顶点A的坐标（2，
），底边OB在x轴上．将△AOB绕点B按顺时针方向旋转一定角度后得△A′O′B，点A的对应点A′在x轴上，则点O′的坐标为（ ）
），底边OB在x轴上．将△AOB绕点B按顺时针方向旋转一定角度后得△A′O′B，点A的对应点A′在x轴上，则点O′的坐标为（ ）A．（ ， ） | B．（ ， ） | C．（，） | D．（，4） |
11．
的倒数是_____ ．
的倒数是12．已知地球的表面积约为510000000km2．数510000000用科学记数法可以表示为______ ．
13．已知正方形ABCD的对角线AC＝
，则正方形ABCD的周长为_____ ．
，则正方形ABCD的周长为14．某学校计划开设A，B，C，D四门校本课程供全体学生选修，规定每人必须并且只能选修其中一门．为了了解各门课程的选修人数，现从全体学生中随机抽取了部分学生进行调查，并把调查结果绘制成如图所示的条形统计图．已知该校全体学生人数为1200名，由此可以估计选修C课程的学生有_____ 人．
15．在△ABC中，AB=AC=5，BC=8，若∠BPC=
∠BAC，tan∠BPC=_______________ ．
∠BAC，tan∠BPC=16．某地准备对一段长120 m的河道进行清淤疏通．若甲工程队先用 4天单独完成其中一部分河道的疏通任务，则余下的任务由乙工程队单独完成需要9天；若甲工程队先单独工作8天，则余下的任务由乙工程队单独完成需要3天．设甲工程队平均每天疏通河道xm，乙工程队平均每天疏通河道y m，则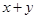
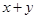的值为_______ ．
的值为17．如图，在矩形ABCD中，
，以点B为圆心，BC长为半径画弧，交边AD于点E，若AE·ED＝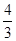
，则矩形ABCD的面积为_____ ．
，以点B为圆心，BC长为半径画弧，交边AD于点E，若AE·ED＝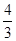
，则矩形ABCD的面积为
18．如图，直线l与半径为4的⊙O相切于点A，P是⊙O上的一个动点（不与点A重合），过点P作PB⊥l，垂足为B，连接PA．设PA＝x，PB＝y，则（x－y）的最大值是 ．
19．计算：
．
．20．解不等式组：
．
．21．先化简，再求值：
，其中
．
，其中．22．解分式方程：
．
．23．如图，在Rt△ABC中，∠ACB＝90°，点D，F分别在AB，AC上，CF＝CB．连接CD，将线段CD绕点C按顺时针方向旋转90°后得CE，连接EF．
（1）求证：△BCD≌△FCE；
（2）若EF∥CD．求∠BDC的度数．
（1）求证：△BCD≌△FCE；
（2）若EF∥CD．求∠BDC的度数．
24．如图，已知函数
的图象与x轴、y轴分别交于点A，B，与函数y＝x的图象交于点M，点M的横坐标为2．在x轴上有一点P (a，0)（其中a>2），过点P作x轴的垂线，分别交函数和y＝x的图象于点C，D
（1）求点A的坐标；
（2）若OB＝CD，求a的值．
的图象与x轴、y轴分别交于点A，B，与函数y＝x的图象交于点M，点M的横坐标为2．在x轴上有一点P (a，0)（其中a>2），过点P作x轴的垂线，分别交函数和y＝x的图象于点C，D（1）求点A的坐标；
（2）若OB＝CD，求a的值．
25．如图，用红、蓝两种颜色随机地对A，B，C三个区域分别进行涂色，每个区域必须涂色并且只能涂一种颜色，请用列举法（画树状图或列表）求A，C两个区域所涂颜色不相同的概率．
26．如图，已知函数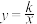
（x>0）的图象经过点A，B，点A的坐标为(1，2)．过点A作AC∥y轴，AC＝1（点C位于点A的下方），过点C作CD∥x轴，与函数的图象交于点D，过点B作BE⊥CD，垂足E在线段CD上，连接OC，OD．
（1）求△OCD的面积；
（2）当BE＝
AC时，求CE的长．
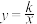（x>0）的图象经过点A，B，点A的坐标为(1，2)．过点A作AC∥y轴，AC＝1（点C位于点A的下方），过点C作CD∥x轴，与函数的图象交于点D，过点B作BE⊥CD，垂足E在线段CD上，连接OC，OD．（1）求△OCD的面积；
（2）当BE＝
AC时，求CE的长．
27．如图，已知⊙O上依次有A，B，C，D四个点，
，连接AB，AD，BD，弦AB不经过圆心O．延长AB到E，使BE＝AB，连接EC，F是EC的中点，连接BF．
（1）若⊙O的半径为3，∠DAB＝120°，求劣弧
的长；
（2）求证：BF＝BD；
（3）设G是BD的中点，探索：在⊙O上是否存在点P（不同于点B），使得PG＝PF?并说明PB与AE的位置关系
，连接AB，AD，BD，弦AB不经过圆心O．延长AB到E，使BE＝AB，连接EC，F是EC的中点，连接BF．（1）若⊙O的半径为3，∠DAB＝120°，求劣弧
的长；（2）求证：BF＝
BD；（3）设G是BD的中点，探索：在⊙O上是否存在点P（不同于点B），使得PG＝PF?并说明PB与AE的位置关系
28．如图，已知l1⊥l2，⊙O与l1，l2都相切，⊙O的半径为2cm．矩形ABCD的边AD，AB分别与l1，l2重合，AB＝
cm，AD＝4cm．若⊙O与矩形ABCD沿l1同时向右移动，⊙O的移动速度为3cm/s，矩形ABCD的移动速度为4cm/s，设移动时间为t(s)．
(1)如图①，连接OA，AC，则∠OAC的度数为 °；
(2)如图②，两个图形移动一段时间后，⊙O到达⊙O1的位置，矩形ABCD到达A1B1C1D1的位置，此时点O1，A1，C1恰好在同一直线上，求圆心O移动的距离(即OO1的长）；
(3)在移动过程中，圆心O到矩形对角线AC所在直线的距离在不断变化，设该距离为d(cm)．当d<2时，求t的取值范围．（解答时可以利用备用图画出相关示意图）
cm，AD＝4cm．若⊙O与矩形ABCD沿l1同时向右移动，⊙O的移动速度为3cm/s，矩形ABCD的移动速度为4cm/s，设移动时间为t(s)．(1)如图①，连接OA，AC，则∠OAC的度数为 °；
(2)如图②，两个图形移动一段时间后，⊙O到达⊙O1的位置，矩形ABCD到达A1B1C1D1的位置，此时点O1，A1，C1恰好在同一直线上，求圆心O移动的距离(即OO1的长）；
(3)在移动过程中，圆心O到矩形对角线AC所在直线的距离在不断变化，设该距离为d(cm)．当d<2时，求t的取值范围．（解答时可以利用备用图画出相关示意图）
29．如图，二次函数
（其中a，m是常数，且a>0，m>0）的图象与x轴分别交于点A，B（点A位于点B的左侧），与y轴交于点C(0，－3)，点D在二次函数的图象上，CD∥AB，连接AD，过点A作射线AE交二次函数的图象于点E，AB平分∠DAE
（1）用含m的代数式表示a；
（2）)求证：
为定值；
（3）设该二次函数图象的顶点为
（其中a，m是常数，且a>0，m>0）的图象与x轴分别交于点A，B（点A位于点B的左侧），与y轴交于点C(0，－3)，点D在二次函数的图象上，CD∥AB，连接AD，过点A作射线AE交二次函数的图象于点E，AB平分∠DAE（1）用含m的代数式表示a；
（2）)求证：
为定值；（3）设该二次函数图象的顶点为
| A．探索：在x轴的负半轴上是否存在点G，连接CF，以线段GF、AD、AE的长度为三边长的三角形是直角三角形？如果存在，只要找出一个满足要求的点G即可，并用含m的代数式表示该点的横坐标；如果不存在，请说明理由． |
