搜索
全一卷
难度系数：0.94 
答案解析
有奖纠错
1．给出四个数0，
，
，-1，其中最小的是（）
，
，-1，其中最小的是（）| A．0 | B． | C． | D．-1 |
2．将一个长方体内部挖去一个圆柱（如图所示），它的主视图是（ ）
A． | B． | C． | D． |
3．某校学生参加体育兴趣小组情况的统计图如图所示，若参加人数最少的小组有25人，则参加人数最多的小组有（ ）
| A．25人 | B．35人 | C．40人 | D．100人 |
4．下列选项中的图形，不属于中心对称图形的是（ ）
| A．等边三角形 | B．正方形 | C．正六边形 | D．圆 |
5．如图，在△ABC中，∠C=90°，AB=5，BC=3，则cosA的值是（ ）
A． | B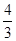． | C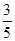． | D． |
6．若关于
的一元二次方程
有两个相等实数根，则
的值是（ ）
的一元二次方程
有两个相等实数根，则
的值是（ ）| A．-1 | B．1 | C．-4 | D．4 |
7．不等式组
的解是（）
的解是（）| A．x＜1 | B．x≥3 | C．1≤x＜3 | D．1＜x≤3 |
8．如图，点
的坐标是
，
是等边三角形，点
在第一象限．若反比例函数
的图象经过点，则
的值是（ ）
的坐标是，是等边三角形，点在第一象限．若反比例函数的图象经过点，则的值是（ ）| A．1 | B．2 | C． | D． |
9．如图，在Rt∠AOB的平分线ON上依次取点C，F，M，过点C作DE⊥OC，分别交OA，OB于点D，
E，以FM为对角线作菱形FGMH，已知∠DFE=∠GFH=120°，FG=FE，设OC=x，图中阴影部分面积为y，则y
与x之间的函数关系式是（ ）
E，以FM为对角线作菱形FGMH，已知∠DFE=∠GFH=120°，FG=FE，设OC=x，图中阴影部分面积为y，则y
与x之间的函数关系式是（ ）
A． | B． | C． | D． |
10．如图，C是以AB为直径的半圆O上一点，连结AC，BC，分别以AC，BC为边向外作正方形ACDE与BCFG，点M，N，P，Q分别是DE，FG，弧AC,弧BC的中点.若MP+NQ=14，AC+BC=18，则AB的长是（ ）
A． | B． | C．13 | D．16 |
11．分解因式：
=___ .
=12．一个不透明的袋子中只装有1个红球和2个蓝球，它们除颜色外其余都相同．现随机从袋中摸出两个球，颜色是一红一蓝的概率是___ .
13． 已知扇形的圆心角为120°，弧长为
，则它的半径为 .
，则它的半径为 .14．方程
的根是___ .
的根是15．某农场拟建两间矩形饲养室，一面靠现有墙（墙足够长），中间用一道墙隔开，并在如图所示的三处各留1m宽的门．已知计划中的材料可建墙体（不包括门）总长为27m，则能建成的饲养室面积最大为________ m2 ．
16．图甲是小明设计的带菱形图案的花边作品，该作品由形如图乙的矩形图案拼接而成（不重叠，无缝隙）．图乙种，
，EF=4cm，上下两个阴影三角形的面积之和为54cm2，其内部菱形由两组距离相等的平行线交叉得到，则该菱形的周长为___ cm
，EF=4cm，上下两个阴影三角形的面积之和为54cm2，其内部菱形由两组距离相等的平行线交叉得到，则该菱形的周长为
17．（本题10分）（1）计算：
（2）化简：
（2）化简：
18．如图，点C，E，F，B在同一直线上，点A，D在BC异侧，AB∥CD，AE=DF，∠A=∠D，
（1）求证：AB=CD；
（2）若AB=CF，∠B=30°，求∠D的度数．
（1）求证：AB=CD；
（2）若AB=CF，∠B=30°，求∠D的度数．
19．某公司需招聘一名员工，对应聘者甲、乙、丙从笔试、面试、体能三个方面进行量化考核．甲、乙、丙各项得分如下表：
（1）根据三项得分的平均分，从高到低确定三名应聘者的排名顺
序．
（2）该公司规定：笔试，面试、体能得分分别不得低于80分，80分，70分，并按60%，30%，10%的比例计入总分．根据规定，请你说明谁将被录用．
| 笔试 | 面试 | 体能 | |
| 甲 | 83 | 79 | 90 |
| 乙 | 85 | 80 | 75 |
| 丙 | 80 | 90 | 73 |
（1）根据三项得分的平均分，从高到低确定三名应聘者的排名顺
序．（2）该公司规定：笔试，面试、体能得分分别不得低于80分，80分，70分，并按60%，30%，10%的比例计入总分．根据规定，请你说明谁将被录用．
20．各顶点都在方格纸格点（横竖格子线的交错点）上的多边形称为格点多边形．如何计算它的面积？奥地利数学家皮克（G•Pick，1859～1942年）证明了格点多边形的面积公式S=a+
b﹣1，其中a表示多边形内部的格点数，b表示多边形边界上的格点数，S表示多边形的面积．如图，a=4，b=6，S=4+×6﹣1=6
（1）请在图中画一个格点正方形，使它的内部只含有4个格点，并写出它的面积．
（2）请在图乙中画一个格点三角形，使它的面积为
，且每条边上除顶点外无其它格点．（注：图甲、图乙在答题纸上）
b﹣1，其中a表示多边形内部的格点数，b表示多边形边界上的格点数，S表示多边形的面积．如图，a=4，b=6，S=4+×6﹣1=6（1）请在图中画一个格点正方形，使它的内部只含有4个格点，并写出它的面积．
（2）请在图乙中画一个格点三角形，使它的面积为
，且每条边上除顶点外无其它格点．（注：图甲、图乙在答题纸上）
21．如图，AB是半圆O的直径，CD⊥AB于点C，交半圆于点E， DF切半圆于点
（1）求证：DF∥AB；
（2）若OC=CE，BF=
，求DE的长．
| A．已知∠AEF=135°． |
（1）求证：DF∥AB；
（2）若OC=CE，BF=
，求DE的长．22．某农业观光园计划将一块面积为900m2的园圃分成A，B，C三个区域，分别种植甲、乙、丙三种花卉，且每平方米栽种甲3株或乙6株或丙12株．已知B区域面积是A的2倍，设A区域面积为
．
（1）求该园圃栽种的花卉总株数
关于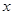
的函数表达式；
（2）若三种花卉共栽种6600株，则A，B，C三个区域的面积分别是多少？
（3）已知三种花卉的单价（都是整数）之和为45元，且差价均不超过10元，在（2）的前提下，全部栽种共需84000元，请写出甲、乙、丙三种花卉中，种植面积最大的花卉总价．
．（1）求该园圃栽种的花卉总株数
关于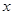
的函数表达式；（2）若三种花卉共栽种6600株，则A，B，C三个区域的面积分别是多少？
（3）已知三种花卉的单价（都是整数）之和为45元，且差价均不超过10元，在（2）的前提下，全部栽种共需84000元，请写出甲、乙、丙三种花卉中，种植面积最大的花卉总价．
23．如图，抛物线
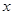交轴正半轴于点A，顶点为M，对称轴NB交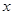轴于点B，过点C（2，0）作射线CD交MB于点D（D在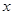轴上方），OE∥CD交MB于点E，EF∥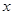轴交CD于点F，作直线M
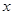交轴正半轴于点A，顶点为M，对称轴NB交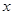轴于点B，过点C（2，0）作射线CD交MB于点D（D在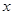轴上方），OE∥CD交MB于点E，EF∥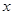轴交CD于点F，作直线MA． （1）求点A，M的坐标； （2）当BD为何值时，点F恰好落在抛物线上？ （3）当BD=1时，①、求直线MF的解析式，并判断点A是否落在该直线上； ②、延长OE交FM于点G，取CF中点P，连结PG，△FPG，四边形DEGP，四边形OCDE的面积分别记为S1，S2，S3，则S1:S2:S3= |
24．如图，点A和动点P在直线l上，点P关于点A的对称点为Q，以AQ为边作Rt△ABQ，使∠BAQ=90°，AQ：AB=3：4，作△ABQ的外接圆O．点C在点P右侧，PC=4，过点C作直线m⊥l，过点O作OD⊥m于点D，交AB右侧的圆弧于点
（1）用关于x的代数式表示BQ，DF．
（2）当点P在点A右侧时，若矩形DEGF的面积等于90，求AP的长．
（3）在点P的整个运动过程中，
①当AP为何值时，矩形DEGF是正方形？
②作直线BG交⊙O于点N，若BN的弦心距为1，求AP的长（直接写出答案）．
A．在射线CD上取点F，使DF=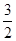 CD，以DE，DF为邻边作矩形DEGF．设AQ=3x． |
（2）当点P在点A右侧时，若矩形DEGF的面积等于90，求AP的长．
（3）在点P的整个运动过程中，
①当AP为何值时，矩形DEGF是正方形？
②作直线BG交⊙O于点N，若BN的弦心距为1，求AP的长（直接写出答案）．
