搜索
全一卷
难度系数：0.94 
答案解析
有奖纠错
1．某市今年1月份某一天的最高气温是3℃，最低气温是—4℃，那么这一天的最高气温比最低气温高
| A．—7℃ | B．7℃ | C．—1℃ | D．1℃ |
2．64的立方根等于
| A．4 | B．—4 | C．8 | D．—8 |
3．已知∠α＝35°19′，则∠α的余角等于（）
| A．144°41′ | B．144°81′ | C．54°41′ | D．54°81′ |
4．根据国家信息产业部2006年5月21日的最新统计，截至2006年4月底，全国电话用户超过7.7亿户．将7.7亿用科学记数法表示为
| A．7.7×1011 | B．7.7×1010 | C．7.7×109 | D．7.7×108 |
5．如图，AB∥CD，直线EF分别交AB，CD于E，F两点，∠BEF的平分线交CD于点G，若∠EFG=72°，则∠EGF等于（ ）
| A．36° | B．54° | C．72° | D．108° |
6．某市对2400名年满15岁的男生的身高进行了测量，结果身高（单位：m）在1.68~1.70这一小组的频率为0.25，则该组的人数为（ ）
| A．600人 | B．150 人 | C．60人 | D．15人 |
7．如图，已知PA是⊙O的切线，A为切点，PC与⊙O相交于B．C两点，PB＝2㎝，BC＝8㎝，则PA的长等于
| A．4㎝ | B．16㎝ |
| C．20㎝ | D．2 ㎝ |
8．二元二次方程组
的解是
的解是A． | B． |
C． | D． |
9．如图，□ABCD的周长是28 cm，△ABC的周长是22cm，则AC的长为（ ）
| A．6 cm | B．12 cm | C．4 cm | D．8 cm |
10．如图为了测量某建筑物AB的高度，在平地上C处测得建筑物顶端A的仰角为30°，沿CB方向前进12 m到达D处，在D处测得建筑物顶端A的仰角为45°，则建筑物AB的高度等于（ ）
A．6（ ＋1）m | B．6 (—1) m |
| C．12 (＋1) m | D．12（－1）m |
11．已知圆锥侧面展开图的圆心角为90°，则该圆锥的底面半径与母线长的比为
| A．1∶2 | B．2∶1 | C．1∶4 | D．4∶1 |
12．已知二次函数
，当自变量
取两个不同的值
时，函数值相等，则当自变量取
时的函数值与
，当自变量
取两个不同的值
时，函数值相等，则当自变量取
时的函数值与A． 时的函数值相等 | B． 时的函数值相等 |
C．  时的函数值相等 | D． x 时的函数值相等 |
13．买一个篮球需要m元，买一个排球需要n元，则买3个篮球和5个排球共需要_____ 元．
14．正六边形的每个内角等于______________ °．
15．在函数
中，自变量x的取值范围是_____________ ．
中，自变量x的取值范围是16．如图，DE与△ABC的边AB，AC分别相交于D，E两点，且DE∥BC．若DE＝2㎝，BC＝3㎝，EC＝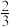
㎝，则AC＝________ ㎝．
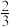㎝，则AC＝
17．用换元法解方程
，若设
，则可得关于的整式方程_______________________ ．
，若设
，则可得关于的整式方程18．如图，直线y ＝kx(k＞0)与双曲线
交于A（x1，y1），B（x2，y2）两点，则2x1y2－7x2y1＝___________ ．
交于A（x1，y1），B（x2，y2）两点，则2x1y2－7x2y1＝
19．（1）计算
（2）解不等式组
（2）解不等式组
20．求作：△ABC的外接圆（要求：用尺规作图，保留作图痕迹，写出作法，不要求证明）．
21．张栋同学到百货大楼买了两种型号的信封，共30个，其中买A型号的信封用了1元5角，买B型号的信封用了1元2角，B型号的信封每个比A型号的信封便宜2分．两种型号的信封的单价各是多少？
22．已知关于x的一元二次方程x2－（m－1）x＋m＋2＝0．
（1）若方程有两个相等的实数根，求m的值；
（2）若方程的两实数根之积等于m2－9m＋2，求
的值．
（1）若方程有两个相等的实数根，求m的值；
（2）若方程的两实数根之积等于m2－9m＋2，求
的值．23． 2006年2月23日《南通日报》公布了2000年~2005年南通市城市居民人均可支配收入情况（如图所示）
根据图示信息：
（1）求南通市城市居民人均可支配收入的中位数；
（2）哪些年份南通市城市居民人均可支配收入比上一年增加了1000元以上？
（3）如果从2006年开始，南通市城市居民人均可支配收入每一年比上一年增加a 元，那么到2008年底可达到18000元，求a的值．
根据图示信息：
（1）求南通市城市居民人均可支配收入的中位数；
（2）哪些年份南通市城市居民人均可支配收入比上一年增加了1000元以上？
（3）如果从2006年开始，南通市城市居民人均可支配收入每一年比上一年增加a 元，那么到2008年底可达到18000元，求a的值．
24．如图，已知AB是⊙O的直径，直线CD与⊙O相切于点C，AC平分∠DAB．
（1）求证：AD⊥DC；
（2）若AD＝2，AC＝
，求AB的长．
（1）求证：AD⊥DC；
（2）若AD＝2，AC＝
，求AB的长．25．已知抛物线y＝ax2＋b x＋c经过A，B，C三点，当x≥0时，其图象如图所示．
（1）求抛物线的解析式，写出抛物线的顶点坐标；
（2）画出抛物线y＝ax2＋b x＋c当x＜0时的图象；
（3）利用抛物线y＝ax2＋b x＋c，写出x为何值时，y＞0．
（1）求抛物线的解析式，写出抛物线的顶点坐标；
（2）画出抛物线y＝ax2＋b x＋c当x＜0时的图象；
（3）利用抛物线y＝ax2＋b x＋c，写出x为何值时，y＞0．
26．已知A＝a＋2，B＝ a2－a＋5，C＝a2＋5a－19，其中a＞2．
（1）求证：B－A＞0，并指出A与B的大小关系；
（2）指出A与C哪个大？说明理由．
（1）求证：B－A＞0，并指出A与B的大小关系；
（2）指出A与C哪个大？说明理由．
27．已知：如图，O为正方形ABCD的中心，BE平分∠DBC，交DC于点E，延长BC到点F，使CF＝CE，连接DF，交BE的延长线于点G，连接OG．
（1）求证：△BCE≌△DCF；
（2）OG与BF有什么数量关系？证明你的结论；
（3）若GE·GB＝4－2
，求正方形ABCD的面积.
（1）求证：△BCE≌△DCF；
（2）OG与BF有什么数量关系？证明你的结论；
（3）若GE·GB＝4－2
，求正方形ABCD的面积. 28．如图，在平面直角坐标系中，O为坐标原点为，B（5,0），M为等腰梯形OBCD底边OB上一点，OD＝BC＝2，∠DMC＝∠DOB＝60°．
（1）求直线CB的解析式；
（2）求点M的坐标；
（3）∠DMC绕点M顺时针旋转α （30°＜α＜60°）后，得到∠D1MC1（点D1，C1依次与点D，C对应），射线MD1交直线DC于点E，射线MC1交直线CB于点F，设DE＝m，BF＝n .求m与 n的函数关系式．
（1）求直线CB的解析式；
（2）求点M的坐标；
（3）∠DMC绕点M顺时针旋转α （30°＜α＜60°）后，得到∠D1MC1（点D1，C1依次与点D，C对应），射线MD1交直线DC于点E，射线MC1交直线CB于点F，设DE＝m，BF＝n .求m与 n的函数关系式．
