全一卷
1.3的相反数是()
| A.﹣3 | B.3 | C. | D.﹣ |
2.下列图形中,既是轴对称图形又是中心对称图形的是( )
A. | B. |
C. | D. |
3.下列运算正确的是( )
A. | B. |
C. | D. |
4.如图是由5个小立方块搭成的几何体的俯视图,小正方形中的数字表示该位置上的小立方块的个数,则这个几何体的主视图是( )


A. | B. | C. | D. |
5.一组数据1,3,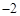 ,3,4的中位数是( )
,3,4的中位数是( )
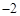 ,3,4的中位数是( )
,3,4的中位数是( )| A.1 | B.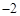 | C. | D.3 |
6.下列调查中,最适合采用全面调查的是( )
| A.对全国中学生视力和用眼卫生情况的调查 |
| B.对某班学生的身高情况的调查 |
| C.对某鞋厂生产的鞋底能承受的弯折次数的调查 |
| D.对某池塘中现有鱼的数量的调查 |
7.若一个等腰三角形的两边长分别为2,4,则第三边的长为( )
| A.2 | B.3 | C.4 | D.2或4 |
8.一副直角三角尺如图摆放,点 在
在 的延长线上,
的延长线上, ,
, ,
, ,
, ,则∠
,则∠ 的度数是( )
的度数是( )

 在
在 的延长线上,
的延长线上, ,
, ,
, ,
, ,则∠
,则∠ 的度数是( )
的度数是( )
A. | B. | C. | D. |
9.如图,AC,BD是四边形ABCD的对角线,点E,F分别是AD,BC的中点,点M,N分别是AC,BD的中点,连接EM,MF,FN,NE,要使四边形EMFN为正方形,则需添加的条件是( )


| A.AB=CD,AB⊥CD | B.AB=CD,AD=BC |
| C.AB=CD,AC⊥BD | D.AB=CD,AD∥BC |
10.如图,在等腰直角三角形ABC中, ,
, ,CH是AB边上的高,正方形DEFG的边DE在高CH上,F,G两点分别在AC,AH上.将正方形DEFG以每秒1cm的速度沿射线DB方向匀速运动,当点G与点B重合时停止运动.设运动时间为ts,正方形DEFG与
,CH是AB边上的高,正方形DEFG的边DE在高CH上,F,G两点分别在AC,AH上.将正方形DEFG以每秒1cm的速度沿射线DB方向匀速运动,当点G与点B重合时停止运动.设运动时间为ts,正方形DEFG与 重叠部分的面积为Scm2,则能反映S与t的函数关系的图象( )
重叠部分的面积为Scm2,则能反映S与t的函数关系的图象( )

 ,
, ,CH是AB边上的高,正方形DEFG的边DE在高CH上,F,G两点分别在AC,AH上.将正方形DEFG以每秒1cm的速度沿射线DB方向匀速运动,当点G与点B重合时停止运动.设运动时间为ts,正方形DEFG与
,CH是AB边上的高,正方形DEFG的边DE在高CH上,F,G两点分别在AC,AH上.将正方形DEFG以每秒1cm的速度沿射线DB方向匀速运动,当点G与点B重合时停止运动.设运动时间为ts,正方形DEFG与 重叠部分的面积为Scm2,则能反映S与t的函数关系的图象( )
重叠部分的面积为Scm2,则能反映S与t的函数关系的图象( )
A. | B. |
C. | D. |
11.据报道,某节日期间某市地铁二号线载客量达到17340000人次,再创历史新高.将数据17340000用科学记数法表示为__________ .
12.不等式组 的解集是__.
的解集是__.
 的解集是__.
的解集是__.13.若关于x的一元二次方程 有实数根,则k的取值范围是________.
有实数根,则k的取值范围是________.
 有实数根,则k的取值范围是________.
有实数根,则k的取值范围是________.14.如果把两条直角边长分别为5,10的直角三角形按相似比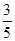 进行缩小,得到的直角三角形的面积是__.
进行缩小,得到的直角三角形的面积是__.
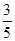 进行缩小,得到的直角三角形的面积是__.
进行缩小,得到的直角三角形的面积是__.15.一个小球在如图所示的方格地板上自由滚动,并随机停留在某块地板上,每块地板大小、质地完全相同,那么该小球停留在黑色区域的概率是__ .


16.如图,矩形 的顶点
的顶点 ,
, 在反比例函数
在反比例函数 的图象上,若点
的图象上,若点 的坐标为
的坐标为 ,
, ,
, 轴,则点
轴,则点 的坐标为
的坐标为__ .

 的顶点
的顶点 ,
, 在反比例函数
在反比例函数 的图象上,若点
的图象上,若点 的坐标为
的坐标为 ,
, ,
, 轴,则点
轴,则点 的坐标为
的坐标为
17.如图,在 中,
中, ,
, ,
, 是
是 所在平面内一点,以
所在平面内一点,以 ,
, ,
, ,
, 为顶点的四边形是平行四边形,则
为顶点的四边形是平行四边形,则 的长为
的长为__ .

 中,
中, ,
, ,
, 是
是 所在平面内一点,以
所在平面内一点,以 ,
, ,
, ,
, 为顶点的四边形是平行四边形,则
为顶点的四边形是平行四边形,则 的长为
的长为
18.如图,直线l1的解析式是 ,直线l2的解析式是
,直线l2的解析式是 ,点A1在l1上,A1的横坐标为
,点A1在l1上,A1的横坐标为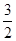 ,作
,作 交l2于点B1,点B2在l2上,以B1A1,B1B2为邻边在直线l1,l2间作菱形A1B1B2C1,分别以点A1,B2为圆心,以A1B1为半径画弧得扇形B1A1C1和扇形B1B2C1,记扇形B1A1C1与扇形B1B2C1重叠部分的面积为S1;延长B2C1交l1于点A2,点B3在l2上,以B2A2,B2B3为邻边在l1,l2间作菱形A2B2B3C2,分别以点A2,B3为圆心,以A2B2为半径画弧得扇形B2A2C2和扇形B2B3C2,记扇形B2A2C2与扇形B2B3C2重叠部分的面积为S2……按照此规律继续作下去,则
交l2于点B1,点B2在l2上,以B1A1,B1B2为邻边在直线l1,l2间作菱形A1B1B2C1,分别以点A1,B2为圆心,以A1B1为半径画弧得扇形B1A1C1和扇形B1B2C1,记扇形B1A1C1与扇形B1B2C1重叠部分的面积为S1;延长B2C1交l1于点A2,点B3在l2上,以B2A2,B2B3为邻边在l1,l2间作菱形A2B2B3C2,分别以点A2,B3为圆心,以A2B2为半径画弧得扇形B2A2C2和扇形B2B3C2,记扇形B2A2C2与扇形B2B3C2重叠部分的面积为S2……按照此规律继续作下去,则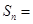 ________.(用含有正整数n的式子表示)
________.(用含有正整数n的式子表示)
 ,直线l2的解析式是
,直线l2的解析式是 ,点A1在l1上,A1的横坐标为
,点A1在l1上,A1的横坐标为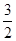 ,作
,作 交l2于点B1,点B2在l2上,以B1A1,B1B2为邻边在直线l1,l2间作菱形A1B1B2C1,分别以点A1,B2为圆心,以A1B1为半径画弧得扇形B1A1C1和扇形B1B2C1,记扇形B1A1C1与扇形B1B2C1重叠部分的面积为S1;延长B2C1交l1于点A2,点B3在l2上,以B2A2,B2B3为邻边在l1,l2间作菱形A2B2B3C2,分别以点A2,B3为圆心,以A2B2为半径画弧得扇形B2A2C2和扇形B2B3C2,记扇形B2A2C2与扇形B2B3C2重叠部分的面积为S2……按照此规律继续作下去,则
交l2于点B1,点B2在l2上,以B1A1,B1B2为邻边在直线l1,l2间作菱形A1B1B2C1,分别以点A1,B2为圆心,以A1B1为半径画弧得扇形B1A1C1和扇形B1B2C1,记扇形B1A1C1与扇形B1B2C1重叠部分的面积为S1;延长B2C1交l1于点A2,点B3在l2上,以B2A2,B2B3为邻边在l1,l2间作菱形A2B2B3C2,分别以点A2,B3为圆心,以A2B2为半径画弧得扇形B2A2C2和扇形B2B3C2,记扇形B2A2C2与扇形B2B3C2重叠部分的面积为S2……按照此规律继续作下去,则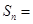 ________.(用含有正整数n的式子表示)
________.(用含有正整数n的式子表示)
19.先化简,再求值: ,其中
,其中 ,
, .
.
 ,其中
,其中 ,
, .
.20.为提升学生的艺术素养,某校计划开设四门选修课程:声乐、舞蹈、书法、摄影.要求每名学生必须选修且只能选修一门课程,为保证计划的有效实施,学校随机对部分学生进行了一次调查,并将调查结果绘制成如下不完整的统计表和统计图.
学生选修课程统计表

根据以上信息,解答下列问题:
(1) ,
, .
.
(2)求出 的值并补全条形统计图.
的值并补全条形统计图.
(3)该校有1500名学生,请你估计选修“声乐”课程的学生有多少名.
(4)七(1)班和七(2)班各有2人选修“舞蹈”课程且有舞蹈基础,学校准备从这4人中随机抽取2人编排“舞蹈”在开班仪式上表演,请用列表法或画树状图的方法求所抽取的2人恰好来自同一个班级的概率.
学生选修课程统计表
课程 | 人数 | 所占百分比 |
声乐 | 14 |
|
舞蹈 | 8 |
|
书法 | 16 |
|
摄影 |
|
|
合计 |
|
|

根据以上信息,解答下列问题:
(1)
 ,
, .
.(2)求出
 的值并补全条形统计图.
的值并补全条形统计图.(3)该校有1500名学生,请你估计选修“声乐”课程的学生有多少名.
(4)七(1)班和七(2)班各有2人选修“舞蹈”课程且有舞蹈基础,学校准备从这4人中随机抽取2人编排“舞蹈”在开班仪式上表演,请用列表法或画树状图的方法求所抽取的2人恰好来自同一个班级的概率.
21.为响应“绿色生活,美丽家园”号召,某社区计划种植甲、乙两种花卉来美化小区环境.若种植甲种花卉 ,乙种花卉
,乙种花卉 ,共需430元;种植甲种花卉
,共需430元;种植甲种花卉 ,乙种花卉
,乙种花卉 ,共需260元.
,共需260元.
(1)求:该社区种植甲种花卉 和种植乙种花卉
和种植乙种花卉 各需多少元?
各需多少元?
(2)该社区准备种植两种花卉共 且费用不超过6300元,那么社区最多能种植乙种花卉多少平方米?
且费用不超过6300元,那么社区最多能种植乙种花卉多少平方米?
 ,乙种花卉
,乙种花卉 ,共需430元;种植甲种花卉
,共需430元;种植甲种花卉 ,乙种花卉
,乙种花卉 ,共需260元.
,共需260元.(1)求:该社区种植甲种花卉
 和种植乙种花卉
和种植乙种花卉 各需多少元?
各需多少元?(2)该社区准备种植两种花卉共
 且费用不超过6300元,那么社区最多能种植乙种花卉多少平方米?
且费用不超过6300元,那么社区最多能种植乙种花卉多少平方米?22.如图,在 中,
中, ,
, ,点
,点 在
在 的内部,
的内部, 经过
经过 ,
, 两点,交
两点,交 于点
于点 ,连接
,连接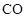 并延长交
并延长交 于点
于点 ,以
,以 ,
, 为邻边作
为邻边作 .
.

(1)判断 与
与 的位置关系,并说明理由.
的位置关系,并说明理由.
(2)若点 是
是 的中点,
的中点, 的半径为2,求
的半径为2,求 的长.
的长.
 中,
中, ,
, ,点
,点 在
在 的内部,
的内部, 经过
经过 ,
, 两点,交
两点,交 于点
于点 ,连接
,连接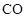 并延长交
并延长交 于点
于点 ,以
,以 ,
, 为邻边作
为邻边作 .
.
(1)判断
 与
与 的位置关系,并说明理由.
的位置关系,并说明理由.(2)若点
 是
是 的中点,
的中点, 的半径为2,求
的半径为2,求 的长.
的长.23.如图,学校教学楼上悬挂一块长为 的标语牌,即
的标语牌,即 .数学活动课上,小明和小红要测量标语牌的底部点
.数学活动课上,小明和小红要测量标语牌的底部点 到地面的距离.测角仪支架高
到地面的距离.测角仪支架高 ,小明在
,小明在 处测得标语牌底部点
处测得标语牌底部点 的仰角为
的仰角为 ,小红在
,小红在 处测得标语牌顶部点
处测得标语牌顶部点 的仰角为
的仰角为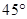 ,
, ,依据他们测量的数据能否求出标语牌底部点
,依据他们测量的数据能否求出标语牌底部点 到地面的距离
到地面的距离 的长?若能,请计算;若不能,请说明理由(图中点
的长?若能,请计算;若不能,请说明理由(图中点 ,
, ,
, ,
, ,
, ,
, ,
,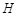 在同一平面内)
在同一平面内)
(参考数据: ,
, ,
,

 的标语牌,即
的标语牌,即 .数学活动课上,小明和小红要测量标语牌的底部点
.数学活动课上,小明和小红要测量标语牌的底部点 到地面的距离.测角仪支架高
到地面的距离.测角仪支架高 ,小明在
,小明在 处测得标语牌底部点
处测得标语牌底部点 的仰角为
的仰角为 ,小红在
,小红在 处测得标语牌顶部点
处测得标语牌顶部点 的仰角为
的仰角为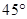 ,
, ,依据他们测量的数据能否求出标语牌底部点
,依据他们测量的数据能否求出标语牌底部点 到地面的距离
到地面的距离 的长?若能,请计算;若不能,请说明理由(图中点
的长?若能,请计算;若不能,请说明理由(图中点 ,
, ,
, ,
, ,
, ,
, ,
,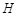 在同一平面内)
在同一平面内)(参考数据:
 ,
, ,
,

24.某网店销售一种儿童玩具,进价为每件30元,物价部门规定每件儿童玩具的销售利润不高于进价的 .在销售过程中发现,这种儿童玩具每天的销售量
.在销售过程中发现,这种儿童玩具每天的销售量 (件
(件 与销售单价
与销售单价 (元
(元 满足一次函数关系.当销售单价为35元时,每天的销售量为350件;当销售单价为40元时,每天的销售量为300件.
满足一次函数关系.当销售单价为35元时,每天的销售量为350件;当销售单价为40元时,每天的销售量为300件.
(1)求 与
与 之间的函数关系式.
之间的函数关系式.
(2)当销售单价为多少时,该网店销售这种儿童玩具每天获得的利润最大,最大利润是多少?
 .在销售过程中发现,这种儿童玩具每天的销售量
.在销售过程中发现,这种儿童玩具每天的销售量 (件
(件 与销售单价
与销售单价 (元
(元 满足一次函数关系.当销售单价为35元时,每天的销售量为350件;当销售单价为40元时,每天的销售量为300件.
满足一次函数关系.当销售单价为35元时,每天的销售量为350件;当销售单价为40元时,每天的销售量为300件.(1)求
 与
与 之间的函数关系式.
之间的函数关系式.(2)当销售单价为多少时,该网店销售这种儿童玩具每天获得的利润最大,最大利润是多少?
25.如图,点E,F分别在正方形ABCD的边CD,BC上,且 ,点P在射线BC上(点P不与点F重合).将线段EP绕点E顺时针旋转
,点P在射线BC上(点P不与点F重合).将线段EP绕点E顺时针旋转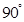 得到线段EG,过点E作GD的垂线QH,垂足为点H,交射线BC于点Q.
得到线段EG,过点E作GD的垂线QH,垂足为点H,交射线BC于点Q.

(1)如图1,若点E是CD的中点,点P在线段BF上,线段BP,QC,EC的数量关系为________.
(2)如图2,若点E不是CD的中点,点P在线段BF上,判断(1)中的结论是否仍然成立.若成立,请写出证明过程;若不成立,请说明理由.
(3)正方形ABCD的边长为6, ,
, ,请直接写出线段BP的长.
,请直接写出线段BP的长.
 ,点P在射线BC上(点P不与点F重合).将线段EP绕点E顺时针旋转
,点P在射线BC上(点P不与点F重合).将线段EP绕点E顺时针旋转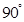 得到线段EG,过点E作GD的垂线QH,垂足为点H,交射线BC于点Q.
得到线段EG,过点E作GD的垂线QH,垂足为点H,交射线BC于点Q.
(1)如图1,若点E是CD的中点,点P在线段BF上,线段BP,QC,EC的数量关系为________.
(2)如图2,若点E不是CD的中点,点P在线段BF上,判断(1)中的结论是否仍然成立.若成立,请写出证明过程;若不成立,请说明理由.
(3)正方形ABCD的边长为6,
 ,
, ,请直接写出线段BP的长.
,请直接写出线段BP的长.26.如图,抛物线 与
与 轴交于
轴交于 ,
, 两点,与
两点,与 轴交于点
轴交于点 ,点
,点 是抛物线的顶点.
是抛物线的顶点.

(1)求抛物线的解析式.
(2)点 是
是 轴负半轴上的一点,且
轴负半轴上的一点,且 ,点
,点 在对称轴右侧的抛物线上运动,连接
在对称轴右侧的抛物线上运动,连接 ,
, 与抛物线的对称轴交于点
与抛物线的对称轴交于点 ,连接
,连接 ,当
,当 平分
平分 时,求点
时,求点 的坐标.
的坐标.
(3)直线 交对称轴于点
交对称轴于点 ,
, 是坐标平面内一点,请直接写出
是坐标平面内一点,请直接写出 与
与 全等时点
全等时点 的坐标.
的坐标.
 与
与 轴交于
轴交于 ,
, 两点,与
两点,与 轴交于点
轴交于点 ,点
,点 是抛物线的顶点.
是抛物线的顶点.
(1)求抛物线的解析式.
(2)点
 是
是 轴负半轴上的一点,且
轴负半轴上的一点,且 ,点
,点 在对称轴右侧的抛物线上运动,连接
在对称轴右侧的抛物线上运动,连接 ,
, 与抛物线的对称轴交于点
与抛物线的对称轴交于点 ,连接
,连接 ,当
,当 平分
平分 时,求点
时,求点 的坐标.
的坐标.(3)直线
 交对称轴于点
交对称轴于点 ,
, 是坐标平面内一点,请直接写出
是坐标平面内一点,请直接写出 与
与 全等时点
全等时点 的坐标.
的坐标. 搜索
搜索
 难度系数:0.94
难度系数:0.94  答案解析
答案解析
 有奖纠错
有奖纠错






