搜索
全一卷
难度系数：0.94 
答案解析
有奖纠错
1．
的倒数是（）
的倒数是（）A． | B． | C． | D． |
2．如图的几何体是由4个完全相同的正方体组成的，这个几何体的左视图是（ ）
A． | B． | C． | D． |
3．在某校开展的“厉行节约，你我有责”活动中，七年级某班对学生7天内收集饮料瓶的情况统计如下（单位：个）：76，90，64，100，84，64，73．则这组数据的众数和中位数分别是（ ）
| A．64，100 | B．64，76 | C．76，64 | D．64，84 |
4．
与
在平面直角坐标系中的位置如图所示，它们关于点
成中心对称，其中点
，则点
的坐标是（）
与
在平面直角坐标系中的位置如图所示，它们关于点
成中心对称，其中点
，则点
的坐标是（）
A． | B． | C． | D． |
5．反比例函数
在每个象限内的函数值
随
的增大而增大，则
的取值范围是（ ）
在每个象限内的函数值
随
的增大而增大，则
的取值范围是（ ）A． | B． | C． | D． |
6．为了节省空间，家里的饭碗一般是摞起来存放的．如果6只饭碗摞起来的高度为15cm，9只饭碗摞起来的高度为20cm，那么11只饭碗摞起来的高度更接近（ ）
| A．21cm | B．22cm | C．23cm | D．24cm |
7．对于一次函数
，下列叙述正确的是（）
，下列叙述正确的是（）A．当 时，函数图象经过第一、二、三象限 |
B．当 时， 随 的增大而减小 |
C．当 时，函数图象一定交于轴的负半轴 |
D．函数图象一定经过点 |
8．在函数
中, 自变量
的取值范围是___________ .
中, 自变量的取值范围是9．任意掷一枚质地均匀的小立方体（立方体的每个面上分别标有数字1，2，3，4，5，6），朝上的面的数字大于2的概率是__________ ．
10．如图，直线
∥
，
，如果
，那么
_______ 度．
∥
，
，如果
，那么
11．如图，
是⊙O的内接三角形，如果
，那么
_______ 度．
是⊙O的内接三角形，如果
，那么
12．已知△ABC∽△DEF，其中AB=5,BC=6,CA=9,DE=3，那么△DEF 的周长是__________ ．
13．如图，将矩形
沿
折叠，点
恰好落在
边上的点
处，如果
，那么
值是__________ ．
沿
折叠，点
恰好落在
边上的点
处，如果
，那么
值是
14．如图，二次函数
的图象经过点
，那么一元二次方程
的根是__________ ．
的图象经过点
，那么一元二次方程
的根是
15．（1）计算：
（2）先化简，再求值：
（2）先化简，再求值：
16．如图，在边长为1的正方形组成的网格中，
的顶点均在格点上，其中点
，将绕点
逆时针旋转
后得到
．
（1）画出
；
（2）在旋转过程中点
所经过的路径长为 ；
（3）求在旋转过程中线段
扫过的图形的面积之和．
的顶点均在格点上，其中点
，将绕点
逆时针旋转
后得到
．（1）画出
；（2）在旋转过程中点
所经过的路径长为 ；（3）求在旋转过程中线段
扫过的图形的面积之和．
17．“小组合作学习”成为我区推动课堂教学改革，打造自主高效课堂的重要举措．某中学从全校学生中随机抽取100人作为样本，对“小组合作学习”实施前后学生的学习兴趣变化情况进行调查分析，统计如下：
请结合图中信息解答下列问题：
（1）小组合作学习前学生学习兴趣为“高”的所占的百分比为 ；
（2）补全小组合作学习后学生学习兴趣的统计图；
（3）通过“小组合作学习”前后学生学习兴趣的对比，请你估计全校2000名学生中学习兴趣获得提高的学生有多少人？
请结合图中信息解答下列问题：
（1）小组合作学习前学生学习兴趣为“高”的所占的百分比为 ；
（2）补全小组合作学习后学生学习兴趣的统计图；
（3）通过“小组合作学习”前后学生学习兴趣的对比，请你估计全校2000名学生中学习兴趣获得提高的学生有多少人？
18．在“玉龙”自行车队的一次训练中，1号队员以高于其他队员10千米/时的速度独自前行，匀速行进一段时间后，又返回队伍，在往返过程中速度保持不变．设分开后行进的时间为x（时），1号队员和其他队员行进的路程分别为y1、y2（千米），并且y1、y2与x的函数关系如图所示：
（1）1号队员折返点A的坐标为 ，如果1号队员与其他队员经过t小时相遇，那么点B的坐标为 ；（用含t的代数式表示）
（2）求1号队员与其他队员经过几小时相遇？
（3）在什么时间内，1号队员与其他队员之间的距离大于2千米？
（1）1号队员折返点A的坐标为 ，如果1号队员与其他队员经过t小时相遇，那么点B的坐标为 ；（用含t的代数式表示）
（2）求1号队员与其他队员经过几小时相遇？
（3）在什么时间内，1号队员与其他队员之间的距离大于2千米？
19．已知，在矩形
中，连接对角线
，将
绕点顺时针旋转
得到
，并将它沿直线
向左平移，直线
与
交于点
，连接
，
．
（1）如图①，当
，点
平移到线段
上时，线段
有怎样的数量关系和位置关系？直接写出你的猜想；
（2）如图②，当，点平移到线段的延长线上时，（1）中的结论是否成立，请说明理由；
（3）如图③，当
时，对矩形进行如已知同样的变换操作，线段有怎样的数量关系和位置关系？直接写出你的猜想．
图① 图② 图③
中，连接对角线
，将
绕点顺时针旋转
得到
，并将它沿直线
向左平移，直线
与
交于点
，连接
，
．（1）如图①，当
，点
平移到线段
上时，线段
有怎样的数量关系和位置关系？直接写出你的猜想；（2）如图②，当
，点平移到线段的延长线上时，（1）中的结论是否成立，请说明理由；（3）如图③，当
时，对矩形进行如已知同样的变换操作，线段有怎样的数量关系和位置关系？直接写出你的猜想．
图① 图② 图③
20．如图，抛物线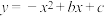
交
轴于点
，交
轴于点
，已知经过点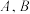
的直线的表达式为
．
（1）求抛物线的函数表达式及其顶点
的坐标；
（2）如图①，点
是线段
上的一个动点，其中
，作直线
轴，交直线
于
，交抛物线于
，作
轴，交直线于点
，四边形
为矩形．设矩形的周长为
，写出与
的函数关系式，并求为何值时周长最大；
（3）如图②，在抛物线的对称轴上是否存在点
，使点
构成的三角形是以为腰的等腰三角形．若存在，直接写出所有符合条件的点的坐标；若不存在，请说明理由．
图① 图②
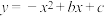交
轴于点
，交
轴于点
，已知经过点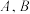
的直线的表达式为
．（1）求抛物线的函数表达式及其顶点
的坐标；（2）如图①，点
是线段
上的一个动点，其中
，作直线
轴，交直线
于
，交抛物线于
，作
轴，交直线于点
，四边形
为矩形．设矩形的周长为
，写出与
的函数关系式，并求为何值时周长最大；（3）如图②，在抛物线的对称轴上是否存在点
，使点
构成的三角形是以为腰的等腰三角形．若存在，直接写出所有符合条件的点的坐标；若不存在，请说明理由．
图① 图②
