全一卷
1.下列计算正确的是()
A. | B. |
C. | D. |
2.如图,直线AB∥CD,∠A=70°,∠C=40°,则∠E等于()


| A.30° | B.40° |
| C.60° | D.70° |
3.下列图形中,既是轴对称图形又是中心对称图形的是



A. | B. | C. | D. |
4.在平面直角坐标系中,点P(-2, +1)所在的象限是( )
+1)所在的象限是( )
 +1)所在的象限是( )
+1)所在的象限是( )| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
5.如图,这是一个正面为黑、反面为白的未拼完的拼木盘,给出如下四块正面为黑、反面为白的拼木,现欲拼满拼木盘使其颜色一致.那么应该选择的拼木是( )


A. | B. | C. | D. |
6.已知 是二元一次方程组
是二元一次方程组 的解,则
的解,则 的值为
的值为

 是二元一次方程组
是二元一次方程组 的解,则
的解,则 的值为
的值为

| A.-1 | B.1 | C.2 | D.3 |
7.如图,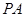 是
是 的切线,切点为A,PA=2
的切线,切点为A,PA=2 ,∠APO=30°,则
,∠APO=30°,则 的半径为( )
的半径为( )

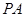 是
是 的切线,切点为A,PA=2
的切线,切点为A,PA=2 ,∠APO=30°,则
,∠APO=30°,则 的半径为( )
的半径为( )
| A.1 | B. |
| C.2 | D.4 |
8.已知反比例函数 ,下列结论中不正确的是()
,下列结论中不正确的是()
 ,下列结论中不正确的是()
,下列结论中不正确的是()| A.图象经过点(-1,-1) | B.图象在第一、三象限 |
C.当 时, 时, | D.当 时, 时, 随着 随着 的增大而增大 的增大而增大 |
9.如图,边长为(m+3)的正方形纸片剪出一个边长为m的正方形之后,剩余部分可剪拼成一个矩形(不重叠无缝隙),若拼成的矩形一边长 为3,则另一边长是( )


| A.m+3 | B.m+6 |
| C.2m+3 | D.2m+6 |
10.如图所示,函数 和
和 的图象相交于(-1,1),(2,2)两点.当
的图象相交于(-1,1),(2,2)两点.当 时,x的取值范围是()
时,x的取值范围是()

 和
和 的图象相交于(-1,1),(2,2)两点.当
的图象相交于(-1,1),(2,2)两点.当 时,x的取值范围是()
时,x的取值范围是()
| A.x<-1 | B.-1<x<2 | C.x>2 | D.x<-1或x>2 |
11.在围棋盒中有x颗白色棋子和y颗黑色棋子,从盒中随机取出一颗棋子,取得白色棋子的概率是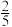 .如果再往盒中放进6颗黑色棋子,取得白色棋子的概率是
.如果再往盒中放进6颗黑色棋子,取得白色棋子的概率是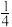 ,则原来盒中有白色棋子( )
,则原来盒中有白色棋子( )
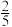 .如果再往盒中放进6颗黑色棋子,取得白色棋子的概率是
.如果再往盒中放进6颗黑色棋子,取得白色棋子的概率是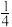 ,则原来盒中有白色棋子( )
,则原来盒中有白色棋子( )| A.8颗 | B.6颗 | C.4颗 | D.2颗 |
12.如图,点 的坐标是
的坐标是 ,若点
,若点 在
在 轴上,且
轴上,且 是等腰三角形,则点
是等腰三角形,则点 的坐标不可能是( )
的坐标不可能是( )

 的坐标是
的坐标是 ,若点
,若点 在
在 轴上,且
轴上,且 是等腰三角形,则点
是等腰三角形,则点 的坐标不可能是( )
的坐标不可能是( )
| A.(2,0) | B.(4,0) |
C.(-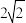 ,0) ,0) | D.(3,0) |
13.若 ,且
,且 ,则m+n=
,则m+n=__ .
 ,且
,且 ,则m+n=
,则m+n=14.如图是由若干个大小相同的小正方体堆砌而成的几何体,那么其三种视图中面积最小的是______ .

15.将一副三角尺如图所示叠放在一起,若 =14cm,则阴影部分的面积是
=14cm,则阴影部分的面积是___ cm2

 =14cm,则阴影部分的面积是
=14cm,则阴影部分的面积是
16.对于任意不相等的两个实数a、b,定义运算※如下:a※b= ,如3※2=
,如3※2= .那么8※12=
.那么8※12=____ .
 ,如3※2=
,如3※2= .那么8※12=
.那么8※12=17.如图,小圆的圆心在原点,半径为3,大圆的圆心坐标为(a,0),半径为5.如果两圆内含,那么a的取值范围是________ .


18.抛物线 上部分点的横坐标
上部分点的横坐标 ,纵坐标
,纵坐标 的对应值如下表:
的对应值如下表:

从上表可知,下列说法中正确的是________ .(填写序号)
①抛物线与 轴的一个交点为(3,0);②函数
轴的一个交点为(3,0);②函数 的最大值为6;
的最大值为6;
③抛物线的对称轴是 ; ④在对称轴左侧,
; ④在对称轴左侧, 随
随 增大而增大.
增大而增大.
 上部分点的横坐标
上部分点的横坐标 ,纵坐标
,纵坐标 的对应值如下表:
的对应值如下表:
从上表可知,下列说法中正确的是
①抛物线与
 轴的一个交点为(3,0);②函数
轴的一个交点为(3,0);②函数 的最大值为6;
的最大值为6;③抛物线的对称轴是
 ; ④在对称轴左侧,
; ④在对称轴左侧, 随
随 增大而增大.
增大而增大.19.先化简,再求值:
 ÷
÷ ·
· ,其中a=-
,其中a=-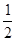 ,b=
,b= .
.
 ÷
÷ ·
· ,其中a=-
,其中a=-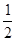 ,b=
,b= .
.20.
某生态示范园要对1号、2号、3号、4号四个新品种共500株果树幼苗进行成活实验,从中选出成活率高的品种进行推广.通过实验得知:3号果树幼苗成活率为89.6%,把实验数据绘制成下列两幅统计图(部分信息未给出).


(1)实验所用的2号果树幼苗的数量是_______株;
(2)求出3号果树幼苗的成活数,并把图2的统计图补充完整;
(3)你认为应选哪一种果树幼苗进行推广?请通过计算说明理由.
某生态示范园要对1号、2号、3号、4号四个新品种共500株果树幼苗进行成活实验,从中选出成活率高的品种进行推广.通过实验得知:3号果树幼苗成活率为89.6%,把实验数据绘制成下列两幅统计图(部分信息未给出).


(1)实验所用的2号果树幼苗的数量是_______株;
(2)求出3号果树幼苗的成活数,并把图2的统计图补充完整;
(3)你认为应选哪一种果树幼苗进行推广?请通过计算说明理由.
21.(本题满分8分)如图,在边长为1的小正方形组成的网格中,△ABC 的三个顶点均在格点上,请按要求完成下列各题:
的三个顶点均在格点上,请按要求完成下列各题:
(1)画线段AD∥BC且使AD =BC,连接CD;
(2)线段AC的长为 ,CD的长为 ,AD的长为 ;
(3)△ACD为 三角形,四边形ABCD的面积为 ;
(4)若E为BC中点,则tan∠CAE的值是 .
 的三个顶点均在格点上,请按要求完成下列各题:
的三个顶点均在格点上,请按要求完成下列各题:(1)画线段AD∥BC且使AD =BC,连接CD;
(2)线段AC的长为 ,CD的长为 ,AD的长为 ;
(3)△ACD为 三角形,四边形ABCD的面积为 ;
(4)若E为BC中点,则tan∠CAE的值是 .

22.某中学为落实市教育局提出的“全员育人,创办特色学校”的会议精神,决心打造“书香校园”,计划用不超过1900本科技类书籍和1620本人文类书籍,组建中、小型两类图书角共30个.已知组建一个中型图书角需科技类书籍80本,人文类书籍50本;组建一个小型图书角需科技类书籍30本,人文类书籍60本.
(1)符合题意的组建方案有几种?请你帮学校设计出来;
(2)若组建一个中型图书角的费用是860元,组建一个小型图书角的费用是570元,试说明(1)中哪种方案费用最低,最低费用是多少元?
(1)符合题意的组建方案有几种?请你帮学校设计出来;
(2)若组建一个中型图书角的费用是860元,组建一个小型图书角的费用是570元,试说明(1)中哪种方案费用最低,最低费用是多少元?
23.如图,点 在
在 的直径
的直径 的延长线上,点
的延长线上,点 在
在 上,且AC=CD,∠ACD=120°.
上,且AC=CD,∠ACD=120°.
(1)求证: 是
是 的切线;
的切线;
(2)若 的半径为2,求图中阴影部分的面积.
的半径为2,求图中阴影部分的面积.

 在
在 的直径
的直径 的延长线上,点
的延长线上,点 在
在 上,且AC=CD,∠ACD=120°.
上,且AC=CD,∠ACD=120°.(1)求证:
 是
是 的切线;
的切线;(2)若
 的半径为2,求图中阴影部分的面积.
的半径为2,求图中阴影部分的面积.
24.如图,直角梯形ABCD中,AD∥BC,∠A=90°, ,
, 交AB于E,DF平分∠EDC交BC于F,连结E
交AB于E,DF平分∠EDC交BC于F,连结E

 ,
, 交AB于E,DF平分∠EDC交BC于F,连结E
交AB于E,DF平分∠EDC交BC于F,连结E| A. (1)证明:  ; ;(2)当   时,求EF的长. 时,求EF的长. |

25.(本题满分10分)如图,在平面直角坐标系 中,把抛物线
中,把抛物线 向左平移1个单位,再向下平移4个单位,得到抛物线
向左平移1个单位,再向下平移4个单位,得到抛物线 .所得抛物线与
.所得抛物线与 轴交于
轴交于 两点(点
两点(点 在点
在点 的左边),与
的左边),与 轴交于点
轴交于点 ,顶点为
,顶点为 .
.
(1)写出 的值;
的值;
(2)判断 的形状,并说明理由;
的形状,并说明理由;
(3)在线段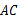 上是否存在点
上是否存在点 ,使
,使 ∽
∽ ?若存在,求出点
?若存在,求出点 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
 中,把抛物线
中,把抛物线 向左平移1个单位,再向下平移4个单位,得到抛物线
向左平移1个单位,再向下平移4个单位,得到抛物线 .所得抛物线与
.所得抛物线与 轴交于
轴交于 两点(点
两点(点 在点
在点 的左边),与
的左边),与 轴交于点
轴交于点 ,顶点为
,顶点为 .
.(1)写出
 的值;
的值;(2)判断
 的形状,并说明理由;
的形状,并说明理由;(3)在线段
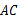 上是否存在点
上是否存在点 ,使
,使 ∽
∽ ?若存在,求出点
?若存在,求出点 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
 搜索
搜索
 难度系数:0.85
难度系数:0.85  答案解析
答案解析
 有奖纠错
有奖纠错
