搜索
全一卷
难度系数：0.94 
答案解析
有奖纠错
1．｜－2015｜等于（）
| A．2015 | B．－2015 | C．±2015 | D． |
2．餐桌边的一蔬一饭，舌尖上的一饮一酌，实属来之不易，舌尖上的浪费让人触目惊心．据统计，中国每年浪费的食物总量折合粮食约500亿千克，这个数据用科学记数法表示为（ ）
| A．5×1010千克 | B．50×109千克 | C．5×109千克 | D．0.5×1011千克 |
3．下列立体图形中，俯视图是正方形的是（ ）
A． | B． | C． | D． |
4．点P（-2，-3）向左平移1个单位，再向上平移3个单位，则所得到的点的坐标为（ ）
| A．（-3，0） | B．（-1，6） | C．（-3，-6） | D．（-1，0） |
5．若一元二次方程x2－2x－m＝0无实数根，则一次函数y＝(m＋1)x＋m－1的图象不经过第( )象限．
| A．四 | B．三 | C．二 | D．一 |
6．如图，点O是矩形ABCD的中心，E是AB上的点，折叠后，点B恰好与点O重合，若BC=3．则折痕CE的长为（）
A． | B． | C． | D．6 |
7．三角形两边的长是3和4，第三边的长是方程x2－12x＋35＝0的根，则该三角形的周长为（ ）
| A．14 | B．12 | C．12或14 | D．以上都不对 |
8．如图，□ABCD中，点E是边AD的中点，EC交对角线BD于点F，则EF:FC等于（ ）
| A．3:2 | B．3:1 | C．1:1 | D．1:2 |
9．如图⊙O的直径
垂直于弦
，垂足是
，
，
，的长为（ ）
垂直于弦
，垂足是
，
，
，的长为（ ）
A． | B．4 | C． | D．8 |
10．如图为二次函数y=ax2+bx+c (a≠0)的图象，则下列说法：①a>0 ②2a+b=0 ③a+b+c>0 ④ 当-1<x<3时，y>0 其中正确的个数为（）
| A．1 | B．2 | C．3 | D．4 |
11．
的平方根是 ．
的平方根是 ．12．计算：
·
．
·
．13．分解因式：
_____ ．
14．一组数据2，3，x，5，7的平均数是4，则这组数据的众数是 ．
15．不等式组
的最小整数解是 ．
的最小整数解是 ．16．如图，在▱ABCD中，AD=2，AB=4，∠A=30°，以点A为圆心，AD的长为半径画弧交AB于点E，连接CE，则阴影部分的面积是 ▲ （结果保留π）．
17．如图，正方形ABCD的边长为4，E为BC上的一点，BE=1，F为AB上的一点，AF=2，P为AC上的一个动点，则PF＋PE 的最小值为______________
18．如图所示是一组有规律的图案，第l个图案由4个基础图形组成，第2个图案由7个基础图形组成，……，第n（n是正整数）个图案中的基础图形个数为_______ （用含n的式子表示）．
19．（本题8分）计算：
20．先化简，再求值：
，其中
.
，其中
.21．“母亲节”前夕，某商店根据市场调查，用3000元购进第一批盒装花，上市后很快售完，接着又用5000元购进第二批这种盒装花．已知第二批所购花的盒数是第一批所购花盒数的2倍，且每盒花的进价比第一批的进价少5元．求第一批盒装花每盒的进价是多少元？
22． 如图，在平面直角坐标系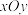
中，一次函数
的图象与反比例函数
的图象交于A（2，3）、B（
，n）两点．
（1）求一次函数和反比例函数的解析式；
（2）若P是
轴上一点，且满足△PAB的面积是5，直接写出OP的长．
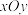中，一次函数
的图象与反比例函数
的图象交于A（2，3）、B（
，n）两点．
（1）求一次函数和反比例函数的解析式；
（2）若P是
轴上一点，且满足△PAB的面积是5，直接写出OP的长．23．某学校为了增强学生体质，决定开设以下体育课外活动项目：A：篮球 B：乒乓球C：羽毛球 D：足球，为了解学生最喜欢哪一种活动项目，随机抽取了部分学生进行调查，并将调查结果绘制成了两幅不完整的统计图，请回答下列问题：
（1）这次被调查的学生共有 人；
（2）请你将条形统计图（2）补充完整；
（3）在平时的乒乓球项目训练中，甲、乙、丙、丁四人表现优秀，现决定从这四名同学中任选两名参加乒乓球比赛，求恰好选中甲、乙两位同学的概率（用树状图或列表法解答）
（1）这次被调查的学生共有 人；
（2）请你将条形统计图（2）补充完整；
（3）在平时的乒乓球项目训练中，甲、乙、丙、丁四人表现优秀，现决定从这四名同学中任选两名参加乒乓球比赛，求恰好选中甲、乙两位同学的概率（用树状图或列表法解答）
24．如图，已知点D在△ABC的BC边上，DE∥AC交AB于E，DF//AB交AC于F
（1）求证：AE=DF，
（2）若AD平分∠BAC，试判断四边形AEDF的形状，并说明理由．
（1）求证：AE=DF，
（2）若AD平分∠BAC，试判断四边形AEDF的形状，并说明理由．
25．如图，等腰三角形ABC中，AC=BC=10，AB=12，以BC为直径作⊙O交AB于点D，交AC于点G，DF⊥AC，垂足为F，交CB的延长线于点E．
（1）求证：直线EF是⊙O的切线；
（2）求cos∠E的值．
（1）求证：直线EF是⊙O的切线；
（2）求cos∠E的值．
26．如图，抛物线
与直线AB交于点A（-1，0），B（4，
）．点D是抛物线A，B两点间部分上的一个动点（不与点A，B重合），直线CD与y轴平行，交直线AB于点C，连接AD，B
与直线AB交于点A（-1，0），B（4，
）．点D是抛物线A，B两点间部分上的一个动点（不与点A，B重合），直线CD与y轴平行，交直线AB于点C，连接AD，BA． （1）求抛物线的解析式； （2）设点D的横坐标为m，△ADB的面积为S，求S关于m 的函数关系式，并求出当S 取最大值时的点C的坐标； |
