搜索
全一卷
难度系数：0.85 
答案解析
有奖纠错
1．
的相反数是（ ）
的相反数是（ ）A． | B． | C．3 | D．-3 |
2．下列运算正确的是（）
| A．x3•x2=x5 | B．（x3）3=x6 | C．x5+x5=x10 | D．x6－x3=x3 |
3．下列图形中，是中心对称图形的是（ ）
A． | B． | C． | D． |
4．下图能说明∠1＞∠2的是【 】
A． | B． | C． | D． |
5．根据下图所示程序计算函数值，若输入的x的值为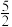
，则输出的函数值为【 】
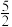，则输出的函数值为【 】
A． | B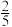． | C． | D． |
6．将点A（2，1）向左平移2个单位长度得到点A′，则点A′的坐标是（ ）
| A．(2，3) | B．（2，－１） | C．（4，1） | D．（0，1） |
7．小明用图中所示的扇形纸片作一个圆锥的侧面，已知扇形的半径为5cm，弧长是
cm，那么这个的圆锥的高是（）
cm，那么这个的圆锥的高是（）
| A．4cm | B．6cm | C．8cm | D．2cm |
8．若
，则
的值为【 】
，则的值为【 】A． | B． | C． | D． |
9．方程
有两个实数根，则k的取值范围是【 】．
有两个实数根，则k的取值范围是【 】．| A．k≥1 | B．k≤1 | C．k>1 | D．k<1 |
10．小英同时掷甲、乙两枚质地均匀的小立方体（立方体的每个面上分别标有数字1，2，3，4，5，6）．记甲立方体朝上一面上的数字为x、乙立方体朝上一面朝上的数字为y，这样就确定点P的一个坐标（
），那么点P落在双曲线
上的概率为（）
），那么点P落在双曲线
上的概率为（）A． | B． | C． | D． |
11． 如图，在直角坐标系中，矩形OABC的顶点O在坐标原点，边OA在x轴上，
OC在y轴上，如果矩形OA′B′C′与矩形OABC关于点O位似，且矩形OA′B′C′的面积等于矩形OABC面积的
，那么点B′的坐标是【 】
OC在y轴上，如果矩形OA′B′C′与矩形OABC关于点O位似，且矩形OA′B′C′的面积等于矩形OABC面积的
，那么点B′的坐标是【 】| A．（－2，3） | B．（2，－3） | C．（3，－2）或（－2，3） | D．（－2，3）或（2，－3） |
12．如图，一次函数
的图象与x轴，y轴交于A，B两点，与反比例函数
的图象相交于C，D两点，分别过C，D两点作y轴，x轴的垂线，垂足为E，F，连接CF，DE．有下列四个结论：①△CEF与△DEF的面积相等；②△AOB∽△FOE；③△DCE≌△CDF；④AC=BD．其中正确的结论是( )
的图象与x轴，y轴交于A，B两点，与反比例函数
的图象相交于C，D两点，分别过C，D两点作y轴，x轴的垂线，垂足为E，F，连接CF，DE．有下列四个结论：①△CEF与△DEF的面积相等；②△AOB∽△FOE；③△DCE≌△CDF；④AC=BD．其中正确的结论是( )
| A．①② | B．①②③ | C．①②③④ | D．②③④ |
13．南海是我国固有领海，她的面积超过东海、黄海、渤海面积的总和，约为360万平方千米，360万用科学记数法可表示为_____ ．
14．分解因式：
=____ .
=15．某校篮球班21名同学的身高如表：
则该校篮球班21名同学身高的中位数是______ cm．
| 身高/cm | 180 | 185 | 187 | 190 | 201 |
| 人数/名 | 4 | 6 | 5 | 4 | 2 |
16．某施工工地安放了一个圆柱形饮水桶的木制支架（如图1），若不计木条的厚度，其俯视图（从上向下垂直投影）如图2所示，已知AD垂直平分BC，AD=BC=48cm，则圆柱形饮水桶的底面半径的最大值是________cm． 
17．在平面直角坐标系xOy中，点A1，A2，A3，···和B1，B2，B3，···分别在直线
和x轴上．△OA1B1，△B1A2B2，△B2A3B3，…都是等腰直角三角形，如果A1（1，1），A2
，那么点
的纵坐标是_________ ．
和x轴上．△OA1B1，△B1A2B2，△B2A3B3，…都是等腰直角三角形，如果A1（1，1），A2
，那么点
的纵坐标是
18．（1）计算：
；
（2）先化简，再求代数式
的值，其中x是不等式组
的整数解．
；（2）先化简，再求代数式
的值，其中x是不等式组
的整数解．19．某校学生会干部对校学生会倡导的“助残”自愿捐款活动进行抽样调查，得到一组学生捐款情况的数据，对学校部分捐款人数进行调查和分组统汁后?将数据整理成如图所示的统计图(图中信息不完整)．已知A、B两组捐款人数的比为1:5
请结合以上信息解答下列问题．
(1)a＝______________，本次调查样本的容量是______________________；
(2)先求出C组的人数，再补全“捐款人数分组统计图1”；
(3)若任意抽出1名学生进行调查，恰好是捐款数不少于30元的概率是多少?
请结合以上信息解答下列问题．
(1)a＝______________，本次调查样本的容量是______________________；
(2)先求出C组的人数，再补全“捐款人数分组统计图1”；
(3)若任意抽出1名学生进行调查，恰好是捐款数不少于30元的概率是多少?
20．如图，AB是⊙O的直径，AM和BN是它的两条切线，DE切⊙O于点E，交AM于点D，交BN于点C，
（1）求证：OD∥BE；
（2）如果OD=6cm，OC=8cm，求CD的长．
（1）求证：OD∥BE；
（2）如果OD=6cm，OC=8cm，求CD的长．
21．如图，长青化工厂与A、B两地有公路、铁路相连．这家工厂从A地购买一批每吨1000元的原料运回工厂，制成每吨8000元的产品运到B地．已知公路运价为1.5元/（吨·千米），铁路运价为1.2元/（吨·千米），且这两次运输共支出公路运输费15000元，铁路运输费97200元．
求：（1）该工厂从A地购买了多少吨原料？制成运往B地的产品多少吨？
（2）这批产品的销售款比原料费与运输费的和多多少元？
求：（1）该工厂从A地购买了多少吨原料？制成运往B地的产品多少吨？
（2）这批产品的销售款比原料费与运输费的和多多少元？
22．如图某天上午9时,向阳号轮船位于A处，观测到某港口城市P位于轮船的北偏西67.5°，轮船以21海里/时的速度向正北方向行驶，下午2时该船到达B处，这时观测到城市P位于该船的南偏西36.9°方向，求此时轮船所处位置B与城市P的距离？（参考数据：sin36.9°≈
，tan36.9°≈
，sin67.5°≈
，tan67.5°≈
）
，tan36.9°≈
，sin67.5°≈
，tan67.5°≈
）
23．（1）如图1，在正方形ABCD中，E是AB上一点，F是AD延长线上一点，且DF＝BE，求证：CE＝CF；
（2）如图2，在正方形ABCD中，E是AB上一点，G是AD上一点，如果∠GCE＝45°，请你利用（1）的结论证明：GE＝BE＋GD；
（3）运用（1）（2）解答中所积累的经验和知识，完成下题：
如图3，在直角梯形ABCD中，AD∥BC（BC＞AD），∠B＝90°，AB＝BC，E是AB上一点，且∠DCE＝45°，BE＝4，DE=10, 求直角梯形ABCD的面积．
（2）如图2，在正方形ABCD中，E是AB上一点，G是AD上一点，如果∠GCE＝45°，请你利用（1）的结论证明：GE＝BE＋GD；
（3）运用（1）（2）解答中所积累的经验和知识，完成下题：
如图3，在直角梯形ABCD中，AD∥BC（BC＞AD），∠B＝90°，AB＝BC，E是AB上一点，且∠DCE＝45°，BE＝4，DE=10, 求直角梯形ABCD的面积．
24．已知抛物线
经过A（2，0）． 设顶点为点P，与x轴的另一交点为点B．
（1）求b的值，求出点P、点B的坐标；
（2）如图，在直线
上是否存在点D，使四边形OPBD为平行四边形？若存在，求出点D的坐
标；若不存在，请说明理由；
（3）在x轴下方的抛物线上是否存在点M，使△AMP≌△AMB？如果存在，试举例验证你的猜想；如果不存在，试说明理由．
经过A（2，0）． 设顶点为点P，与x轴的另一交点为点B．（1）求b的值，求出点P、点B的坐标；
（2）如图，在直线
上是否存在点D，使四边形OPBD为平行四边形？若存在，求出点D的坐标；若不存在，请说明理由；
（3）在x轴下方的抛物线上是否存在点M，使△AMP≌△AMB？如果存在，试举例验证你的猜想；如果不存在，试说明理由．
