搜索
全一卷
难度系数：0.94 
答案解析
有奖纠错
1．﹣
的倒数是（）
的倒数是（）| A．﹣ | B． | C．﹣5 | D．5 |
2．使代数式
有意义的x的取值范围是（）
有意义的x的取值范围是（）| A．x≥0 | B．﹣5≤x＜5 | C．x≥5 | D．x≥﹣5 |
3．下列图形一定是轴对称图形的是（ ）
| A．平行四边形 | B．正方形 | C．三角形 | D．梯形 |
4．将数据37000用科学记数法表示为3.7×10n，则n的值为（ ）
| A．3 | B．4 | C．5 | D．6 |
5．如图，一个简单几何体的三视图的主视图与左视图都为正三角形，其俯视图为正方形，则这个几何体是（ ）
| A．四棱锥 | B．正方体 | C．四棱柱 | D．三棱锥 |
6．下列运算结果正确的是（）
| A．a2•a3=a6 | B．（a2）3=a5 | C．x6÷x2=x4 | D．a2+a5=2a3 |
7．在平面直角坐标系中，反比例函数y=
的图象的两支分别在（ ）
的图象的两支分别在（ ）| A．第一、三象限 | B．第一、二象限 |
| C．第二、四象限 | D．第三、四象限 |
8．一元二次方程x2+px﹣2=0的一个根为2，则p的值为（ ）
| A．1 | B．2 | C．﹣1 | D．﹣2 |
9．如图，圆锥模具的母线长为10cm，底面半径为5cm，则这个圆锥模具的侧面积是（）
| A．10πcm2 | B．50πcm2 | C．100πcm2 | D．150πcm2 |
10．不等式
的解是_______ ．
的解是11．如图，点A，B，C在圆O上，OC⊥AB，垂足为D，若⊙O的半径是10cm，AB=12cm，则CD=___ cm．
12．已知一组数据1，2，x，2，3，3，5，7的众数是2，则这组数据的中位数是 ．
13．从0，1，2这三个数中任取一个数作为点P的横坐标，再从剩下的两个数中任取一个数作为点P的纵坐标，则点P落在抛物线y=﹣x2+x+2上的概率为 ．
14．（1）计算：
+|
﹣1|+（
）﹣1﹣2sin45°；
（2）解方程组：
．
+|
﹣1|+（
）﹣1﹣2sin45°；（2）解方程组：
．15．先化简，再求值：
﹣
，其中a=
+1，b=﹣1．
﹣
，其中a=
+1，b=﹣1．16．为了了解某地初中三年级学生参加消防知识竞赛成绩（均为整数），从中抽取了1%的同学的竞赛成绩，整理后绘制了如下的频数分布直方图，请结合图形解答下列问题：
（1）指出这个问题中的总体；
（2）求竞赛成绩在84.5﹣89.5这一小组的频率；
（3）如果竞赛成绩在90分以上（含90分）的同学可以获得奖励，请估计该地初三年级约有多少人获得奖励．
（1）指出这个问题中的总体；
（2）求竞赛成绩在84.5﹣89.5这一小组的频率；
（3）如果竞赛成绩在90分以上（含90分）的同学可以获得奖励，请估计该地初三年级约有多少人获得奖励．
17．如图，在△ABC中，∠ABC=90°，∠A=30°，D是边AB上一点，∠BDC=45°，AD=4，求BC的长．（结果保留根号）
18．如图，在△AOB中，∠ABO=90°，OB=4，AB=8，反比例函数y=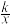
在第一象限内的图象分别交OA，AB于点C和点D，且△BOD的面积S△BOD=4．
（1）求反比例函数解析式；
（2）求点C的坐标．
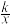在第一象限内的图象分别交OA，AB于点C和点D，且△BOD的面积S△BOD=4．（1）求反比例函数解析式；
（2）求点C的坐标．
19．如图，在▱ABCD中，E，F分别为BC，AB中点，连接FC，AE，且AE与FC交于点G，AE的延长线与DC的延长线交于点N．
（1）求证：△ABE≌△NCE；
（2）若AB=3n，FB=
GE，试用含n的式子表示线段AN的长．
（1）求证：△ABE≌△NCE；
（2）若AB=3n，FB=
GE，试用含n的式子表示线段AN的长．
20．已知a+b=3，ab=2，则代数式（a﹣2）（b﹣2）的值是__ ．
21．设a，b，c，d为实数，现规定一种新的运算
=ad﹣bc，则满足等式
=1的x的值为__ ．
=ad﹣bc，则满足等式
=1的x的值为22．给出下列函数：①y=2x﹣1；②y=
；③y=﹣x2．从中任取一个函数，取出的函数符合条件“当x＞1时，函数值y随x增大而减小”的概率是 ．
；③y=﹣x2．从中任取一个函数，取出的函数符合条件“当x＞1时，函数值y随x增大而减小”的概率是 ．23．已知抛物线y=x2﹣k的顶点为P，与x轴交于点A，B，且△ABP是正三角形，则k的值是___
24．如图，我国古代数学家得出的“赵爽弦图”是由四个全等的直角三角形和一个小正方形密铺构成的大正方形，若小正方形与大正方形的面积之比为1：13，则直角三角形较短的直角边a与较长的直角边b的比值为 ．
25．已知某工厂计划用库存的302m3木料为某学校生产500套桌椅，供该校1250名学生使用，该厂生产的桌椅分为A，B两种型号，有关数据如下：
设生产A型桌椅x（套），生产全部桌椅并运往该校的总费用（总费用=生产成本+运费）为y元．
（1）求y与x之间的关系式，并指出x的取值范围；
（2）当总费用y最小时，求相应的x值及此时y的值．
| 桌椅型号 | 一套桌椅所坐学生人数（单位：人） | 生产一套桌椅所需木材（单位：m3） | 一套桌椅的生产成本（单位：元） | 一套桌椅的运费（单位：元） |
| A | 2 | 0.5 | 100 | 2 |
| B | 3 | 0.7 | 120 | 4 |
设生产A型桌椅x（套），生产全部桌椅并运往该校的总费用（总费用=生产成本+运费）为y元．
（1）求y与x之间的关系式，并指出x的取值范围；
（2）当总费用y最小时，求相应的x值及此时y的值．
26．如图，在△ABC中，∠ABC＝90°，以AB的中点O为圆心，OA为半径的圆交AC于点D，E是BC的中点，连接DE，O
| A． （1）判断DE与⊙O的位置关系，并说明理由； （2）求证：BC2＝2CD•OE； （3）若  ，求OE的长． |
27．在平面直角坐标系xOy中（O为坐标原点），已知抛物线y=x2+bx+c过点A（4，0），B（1，﹣3）．
（1）求b，c的值，并写出该抛物线的对称轴和顶点坐标；
（2）设抛物线的对称轴为直线l，点P（m，n）是抛物线上在第一象限的点，点E与点P关于直线l对称，点E与点F关于y轴对称，若四边形OAPF的面积为48，求点P的坐标；
（3）在（2）的条件下，设M是直线l上任意一点，试判断MP+MA是否存在最小值？若存在，求出这个最小值及相应的点M的坐标；若不存在，请说明理由．
（1）求b，c的值，并写出该抛物线的对称轴和顶点坐标；
（2）设抛物线的对称轴为直线l，点P（m，n）是抛物线上在第一象限的点，点E与点P关于直线l对称，点E与点F关于y轴对称，若四边形OAPF的面积为48，求点P的坐标；
（3）在（2）的条件下，设M是直线l上任意一点，试判断MP+MA是否存在最小值？若存在，求出这个最小值及相应的点M的坐标；若不存在，请说明理由．
