搜索
全一卷
难度系数：0.94 
答案解析
有奖纠错
1．
的倒数是（ ）
的倒数是（ ）| A．5 | B． | C． | D． |
2．在第三届中小学生运动会上，我市共有1330名学生参赛，创造了比赛组别、人数、项目之最，将1330用科学记数法表示为（ ）
| A．133×10 | B．1.33×103 | C．133×104 | D．133×105 |
3．下列运算正确的是（）
A． | B． | C． | D． |
4．在市委、市府的领导下，全市人民齐心协力，将广安成功地创建为“全国文明城市”，为此小红特制了一个正方体玩具，其展开图如图所示，原正方体中与“文”字所在的面上标的字应是（ ）
| A．全 | B．明 | C．城 | D．国 |
5．下列四个图形中，线段BE是△ABC的高的是（ ）
A． | B． | C． | D． |
6．下列说法错误的是（）
| A．“伊利”纯牛奶消费者服务热线是4008169999，该十个数的中位数为7 |
| B．服装店老板最关心的是卖出服装的众数 |
| C．要了解全市初三近4万名学生2015年中考数学成绩情况，适宜采用全面调查 |
| D．条形统计图能够显示每组中的具体数据，易于比较数据之间的差别 |
7．如图，数轴上表示的是某个函数自变量的取值范围，则这个函数解析式为（ ）
| A．y=x+2 | B．y=x2+2 | C．y= | D．y= |
8．一个等腰三角形的两条边长分别是方程
的两根，则该等腰三角形的周长是（ ）
的两根，则该等腰三角形的周长是（ ）| A．12 | B．9 | C．13 | D．12或9 |
9．某油箱容量为60 L的汽车，加满汽油后行驶了100 Km时，油箱中的汽油大约消耗了
，如果加满汽油后汽车行驶的路程为x Km，邮箱中剩油量为y L，则y与x之间的函数解析式和自变量取值范围分别是（）
，如果加满汽油后汽车行驶的路程为x Km，邮箱中剩油量为y L，则y与x之间的函数解析式和自变量取值范围分别是（）| A．y=0.12x，x＞0 | B．y=60﹣0.12x，x＞0 | C．y=0.12x，0≤x≤500 | D．y=60﹣0.12x，0≤x≤500 |
10．如图，抛物线
过点
和点
，且顶点在第四象限，设
，则
的取值范围是（ ）．
过点和点，且顶点在第四象限，设，则的取值范围是（ ）．A． | B． | C． | D． |
11．如果点M（3，x）在第一象限，则x的取值范围是_________ ．
12．如图，A、B、C三点在⊙O上，且∠AOB=70°，则∠C =________ 度．
13．实数a在数轴的位置如图所示，则
=_________ ．
=
14．不等式组
的所有整数解的积为__________ ．
的所有整数解的积为15．如图，已知E、F、G、H分别为菱形ABCD四边的中点，AB=6cm，∠ABC=60°，则四边形EFGH的面积为__ cm2．
16．如图，半径为r的⊙O分别绕面积相等的等边三角形、正方形和圆用相同速度匀速滚动一周，用时分别为
、
、
，则、、的大小关系为_____________ ．
、
、
，则、、的大小关系为
17．（5分）计算：
．
．18．解方程：
．
．19．在平行四边形ABCD中，将△BCD沿BD翻折，使点C落在点E处，BE和AD相交于点O，求证：OA=OE．
20．如图，一次函数的图象与x轴、y轴分别相交于A、B两点，且与反比例函数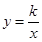
（
）的图象在第一象限交于点C，如果点B的坐标为（0，2），OA=OB，B是线段AC的中点．
（1）求点A的坐标及一次函数解析式．
（2）求点C的坐标及反比例函数的解析式．
（
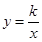）的图象在第一象限交于点C，如果点B的坐标为（0，2），OA=OB，B是线段AC的中点．
（1）求点A的坐标及一次函数解析式．
（2）求点C的坐标及反比例函数的解析式．
21．“阳光体育”运动关乎每个学生未来的幸福生活，今年五月，我市某校开展了以“阳光体育我是冠军”为主题的一分钟限时跳绳比赛，要求每个班选2﹣3名选手参赛，现将80名选手比赛成绩（单位：次/分钟）进行统计．绘制成频数分布直方图，如图所示．
（1）图中a值为 ．
（2）将跳绳次数在160～190的选手依次记为A1、A2、…An，从中随机抽取两名选手作经验交流，请用树状或列表法求恰好抽取到的选手A1和A2的概率．
（1）图中a值为 ．
（2）将跳绳次数在160～190的选手依次记为A1、A2、…An，从中随机抽取两名选手作经验交流，请用树状或列表法求恰好抽取到的选手A1和A2的概率．
22．数学活动课上，老师和学生一起去测量学校升旗台上旗杆AB的高度，如图，老师测得升旗台前斜坡FC的坡比为iFC=1：10（即EF：CE=1：10），学生小明站在离升旗台水平距离为35m（即CE=35m）处的C点，测得旗杆顶端B的仰角为α，已知tanα=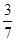
，升旗台高AF=1m，小明身高CD=1.6m，请帮小明计算出旗杆AB的高度．
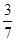，升旗台高AF=1m，小明身高CD=1.6m，请帮小明计算出旗杆AB的高度．
23．手工课上，老师要求同学们将边长为4cm的正方形纸片恰好剪成六个等腰直角三角形，聪明的你请在下列四个正方形中画出不同的剪裁线，并直接写出每种不同分割后得到的最小等腰直角三角形面积（注：不同的分法，面积可以相等）
24．如图，PB为☉O的切线，B为切点，过B作OP的垂线BA，垂足为C，交☉O于点A，连接PA，AO.并延长AO交☉O于点E，与PB的延长线交于点
A． (1)求证：PA是☉O的切线； (2)若  = ，且OC=4，求PA的长和tan D的值. |
25．（10分）如图，边长为1的正方形ABCD一边AD在x负半轴上，直线l：
经过点B（x，1）与x轴，y轴分别交于点H，F，抛物线
顶点E在直线l上．
（1）求A，D两点的坐标及抛物线经过A，D两点时的解析式；
（2）当抛物线的顶点E（m，n）在直线l上运动时，连接EA，ED，试求△EAD的面积S与m之间的函数解析式，并写出m的取值范围；
（3）设抛物线与y轴交于G点，当抛物线顶点E在直线l上运动时，以A，C，E，G为顶点的四边形能否成为平行四边形？若能，求出E点坐标；若不能，请说明理由．
经过点B（x，1）与x轴，y轴分别交于点H，F，抛物线
顶点E在直线l上．
（1）求A，D两点的坐标及抛物线经过A，D两点时的解析式；
（2）当抛物线的顶点E（m，n）在直线l上运动时，连接EA，ED，试求△EAD的面积S与m之间的函数解析式，并写出m的取值范围；
（3）设抛物线与y轴交于G点，当抛物线顶点E在直线l上运动时，以A，C，E，G为顶点的四边形能否成为平行四边形？若能，求出E点坐标；若不能，请说明理由．
